Świetnie, odznaka %% zdobyta
Twierdzenie Pitagorasa » Decydowanie »
Przejdź do tematu:
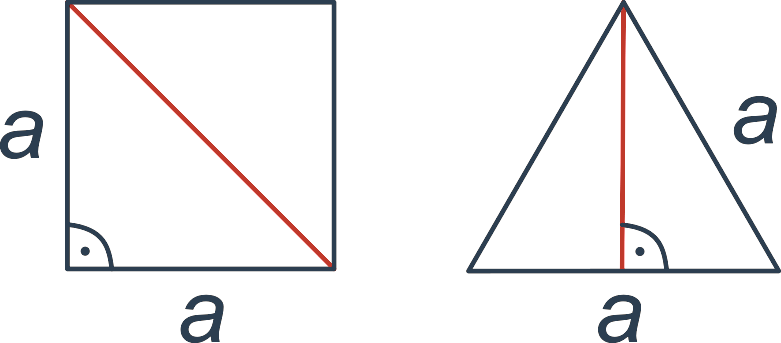
Twierdzenie Pitagorasa
Twierdzenie Pitagorasa
Przejdź do ćwiczenia:
Decydowanie
Decydowanie
Włącz widok pełnoekranowy
Pokaż wyjaśnienie do tematu
Udostępnij
Pokaż ustawienia ćwiczenia
kod QR
Możesz zeskanować kod QR np. za pomocą telefonu komórkowego i w ten sposób przejść bezpośrednio do danego ćwiczenia lub zestawu.
Kod / krótki adres
Trzyznakowy kod możesz wpisać w pasku wyszukiwania, jest on jednocześnie częścią skróconego adresu.
Skopiuj kliknięciem.
FPE
Ustawienia ćwiczenia
Uwaga, ustawienia dotyczą wyłącznie danego ćwiczenia i przedmiotu.
Twierdzenie Pitagorasa: zastosowanie (średnie)