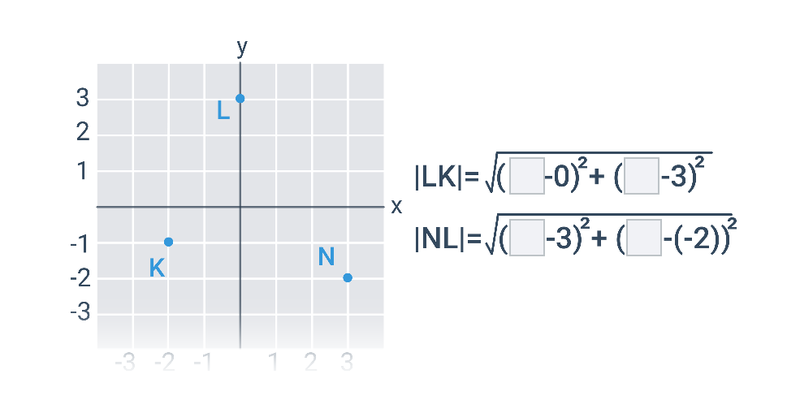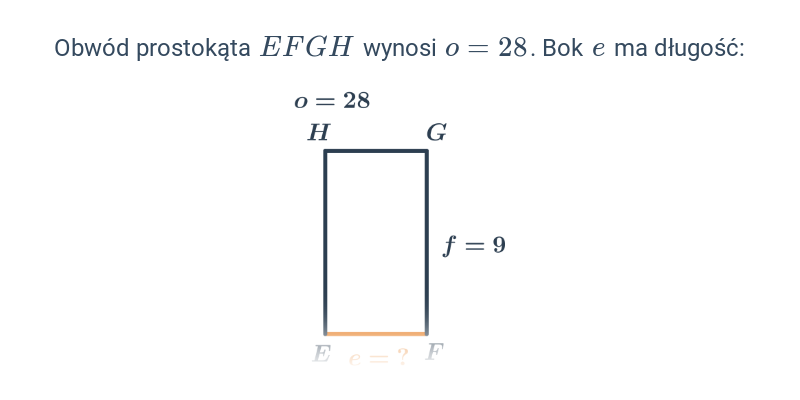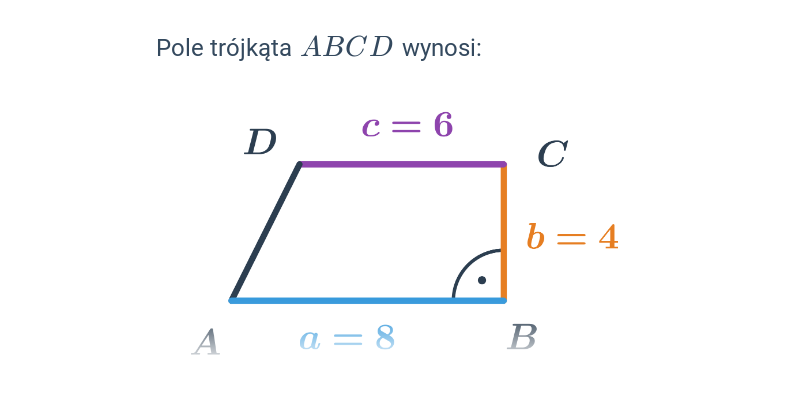Geometria
Orientacja przestrzenna
Orientacja przestrzenna na płaszczyźnie
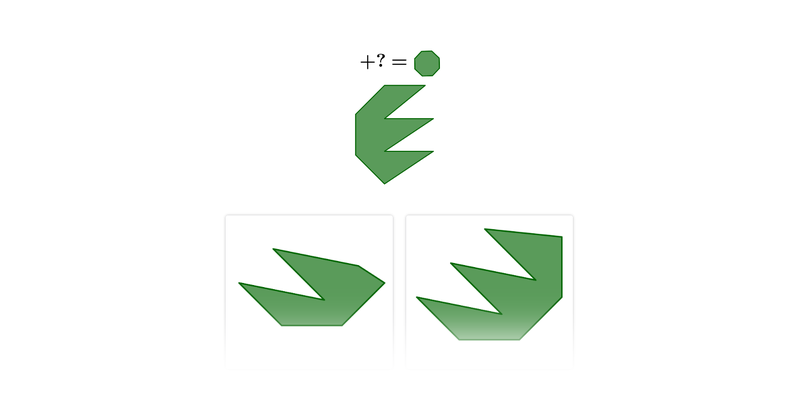
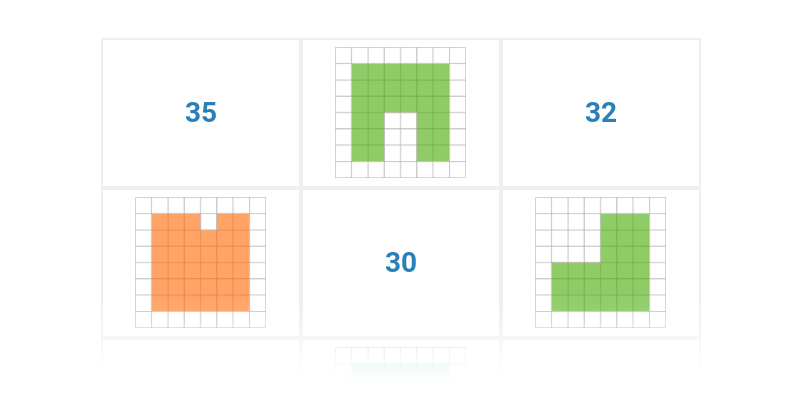
Uzupełnianie figur
Obrót i odbicie na płaszczyźnie
Orientacja przestrzenna: obiekty 3D
Obiekty 3D z różnych rzutów
Drut w przeźroczystym obiekcie
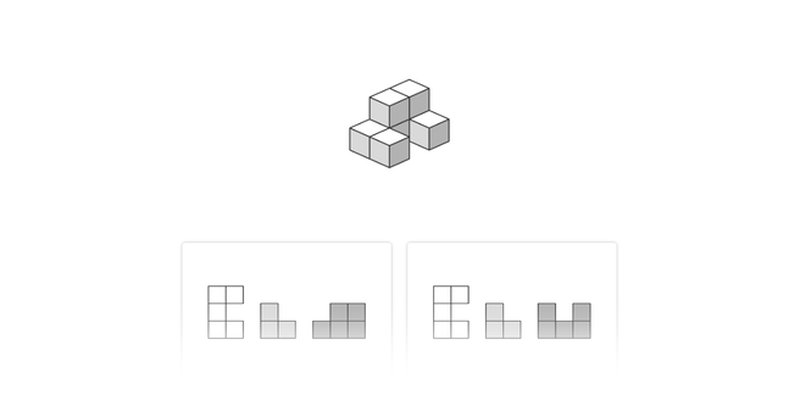
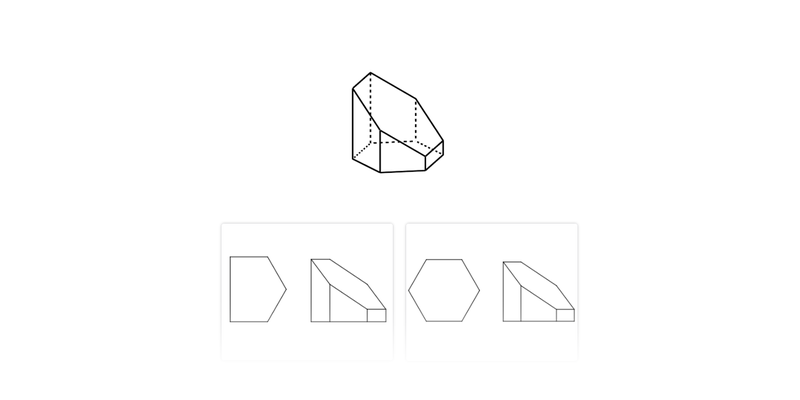
Rzut z przodu, z góry, z boku

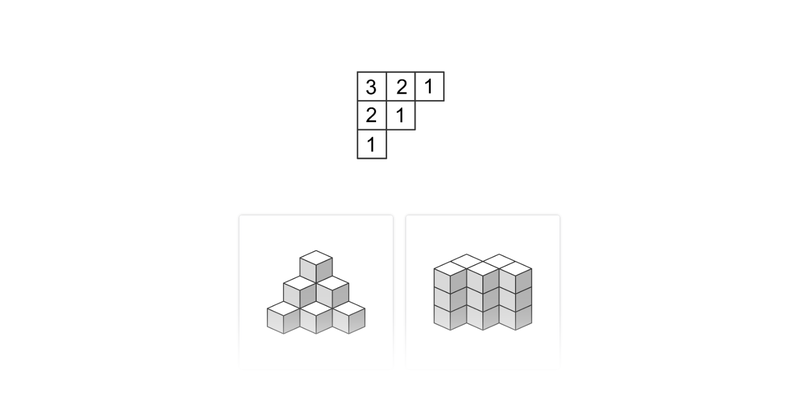
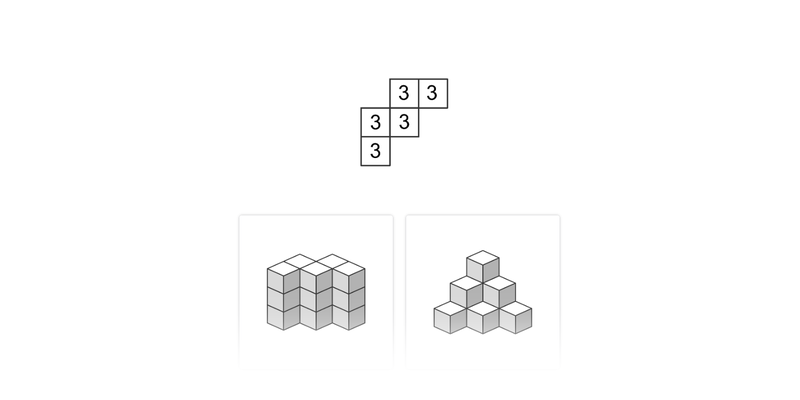
Klocki: plan budowli
Budowle z klocków: widok z boku
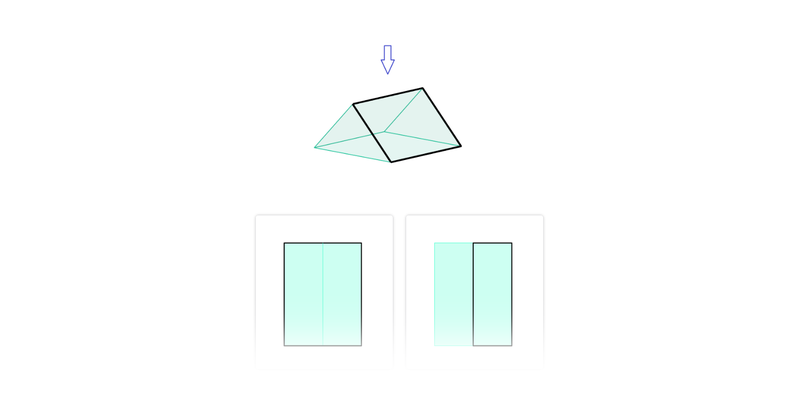
Rzut z przodu i z góry
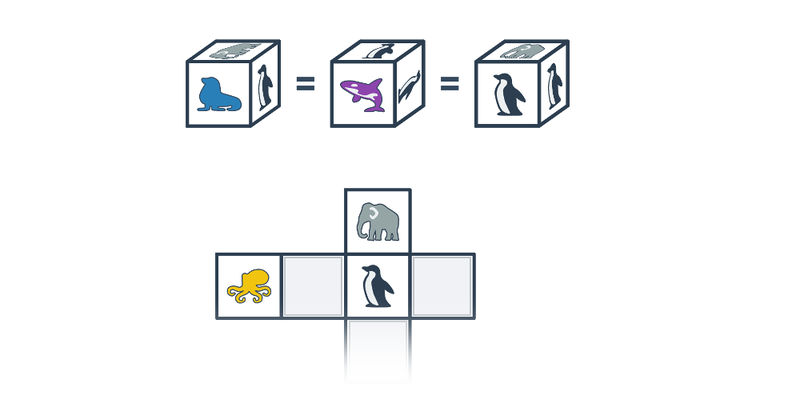
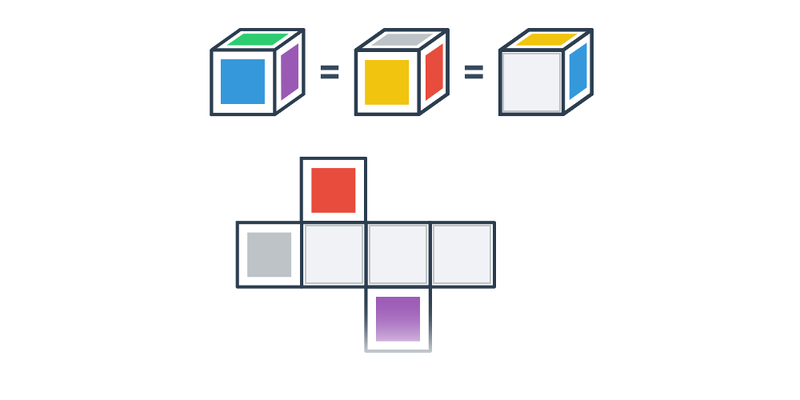
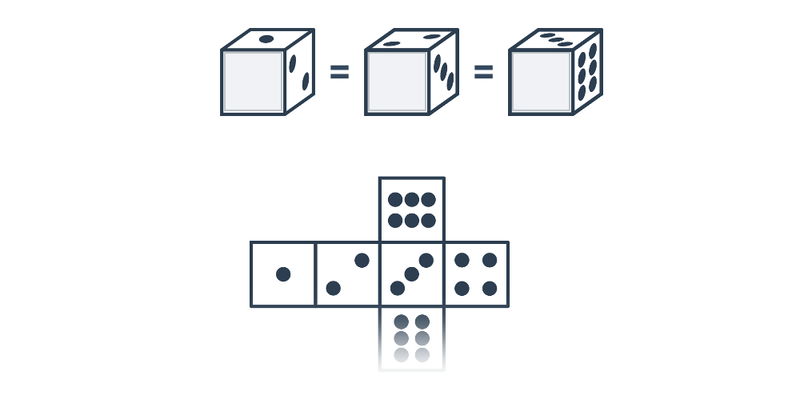
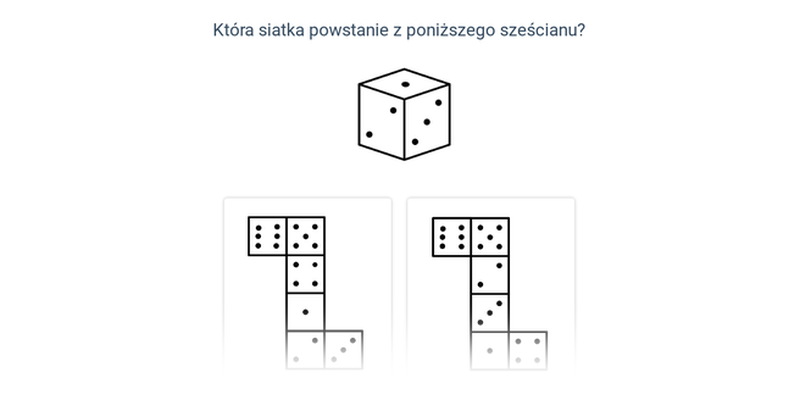
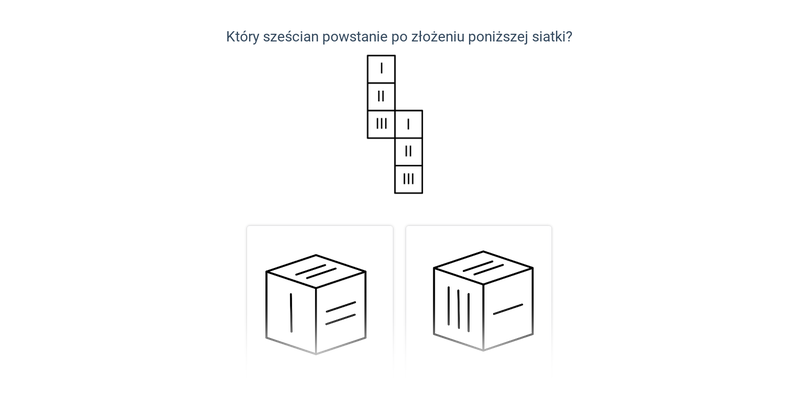
Siatka sześcianu

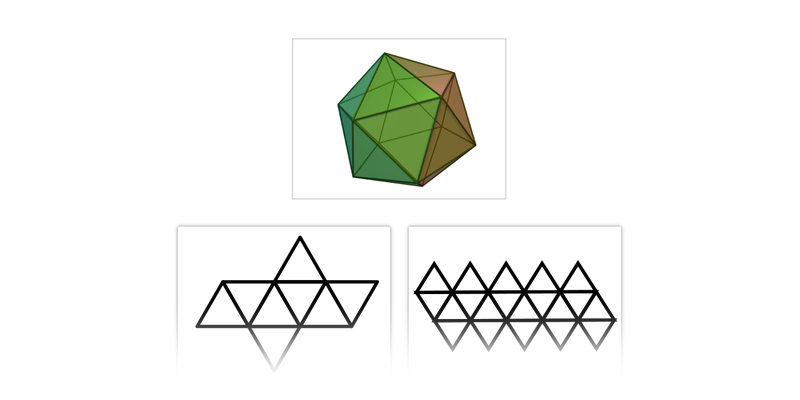
Siatki brył

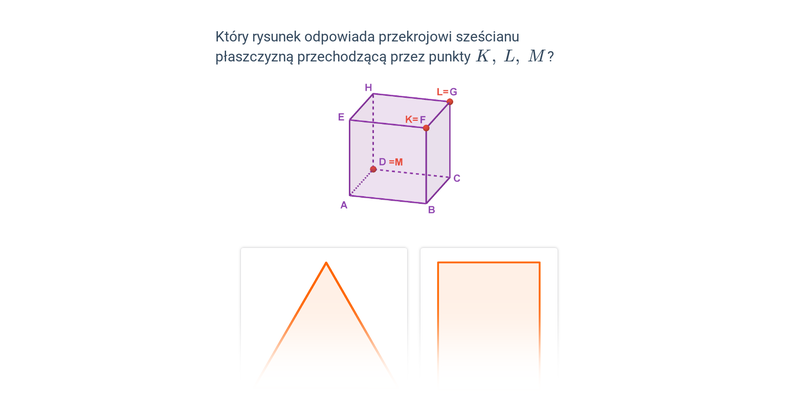
Przekroje sześcianu
Przekroje brył
Orientacja przestrzenna: miks przykładów
Pojęcia geometryczne
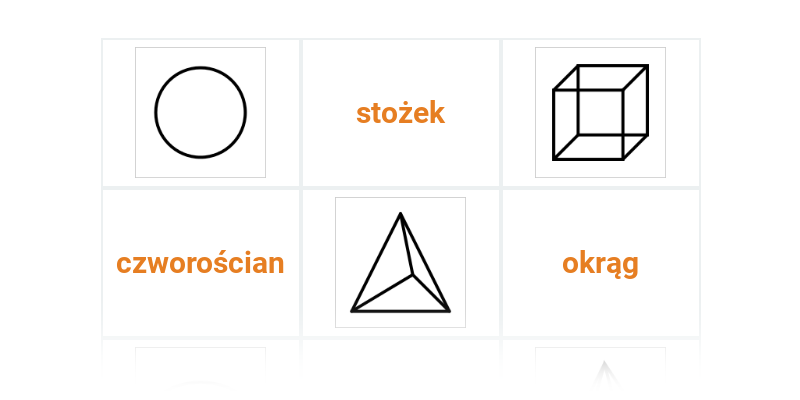
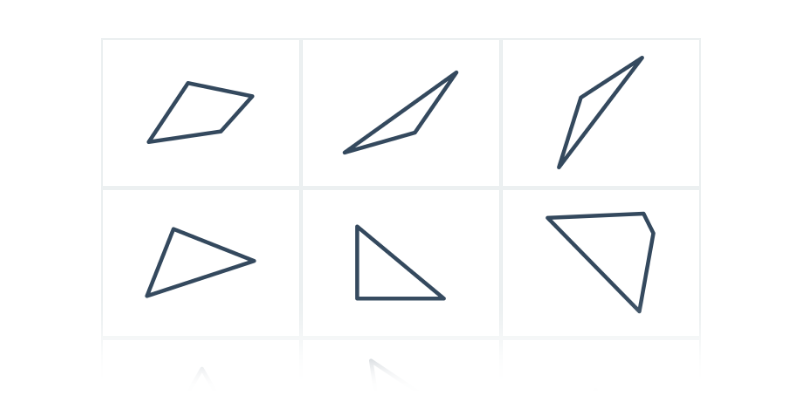
Nazwy figur i brył geometrycznych
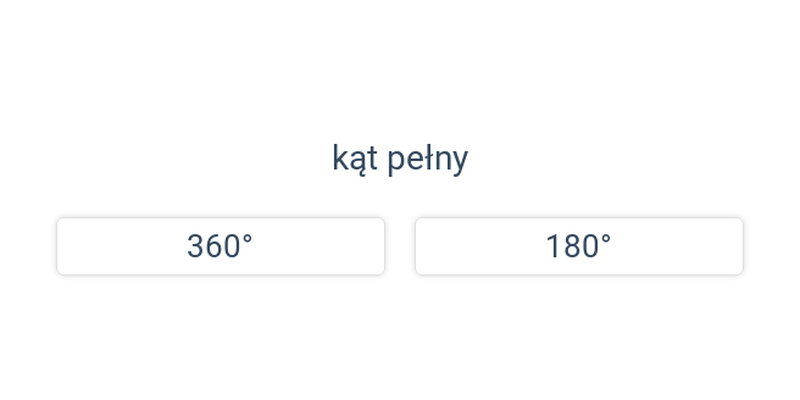
Pojęcia związane z kątami
Pojęcia: oznaczenia kątów
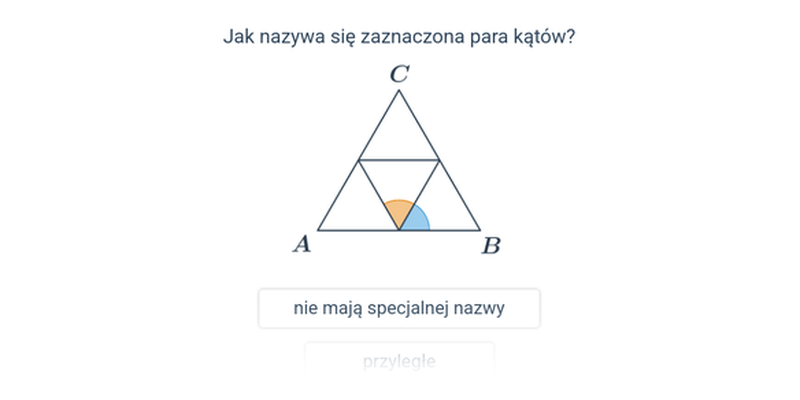
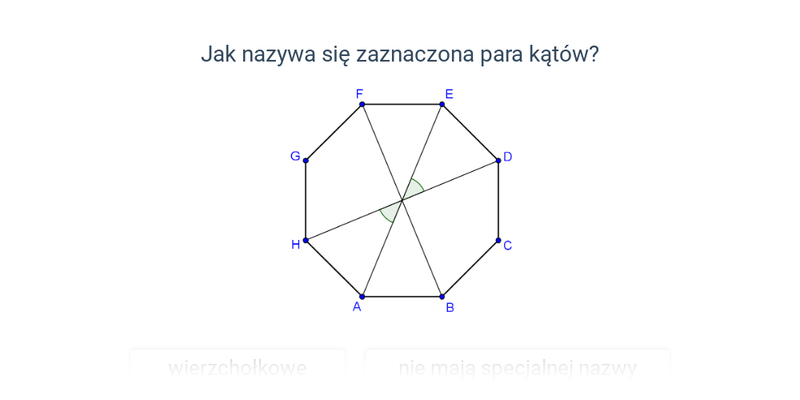
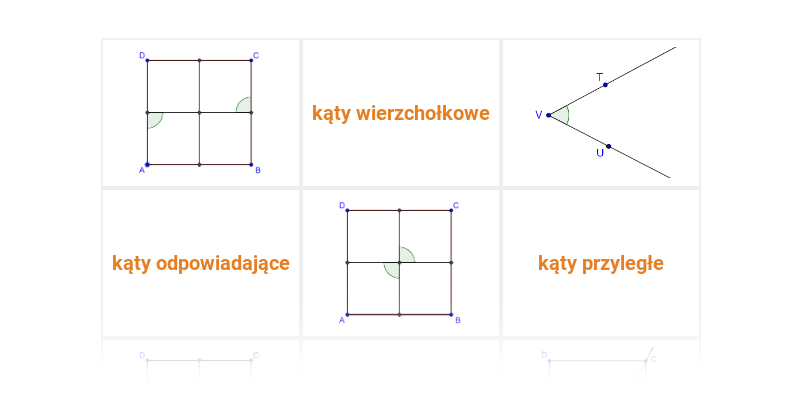
Pary kątów: kąty wierzchołkowe i przyległe
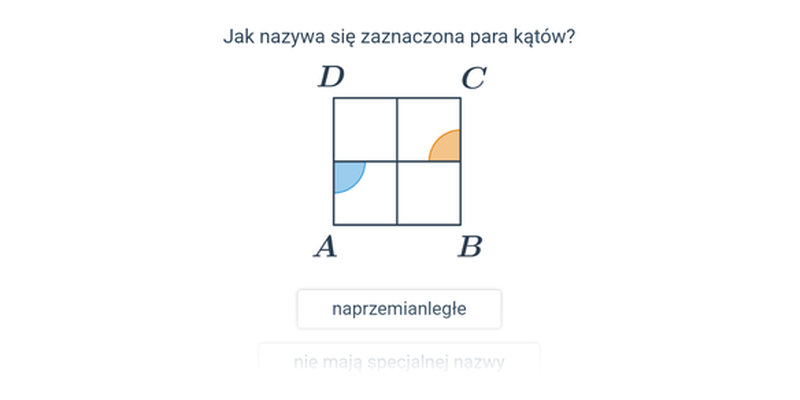
Pary kątów: kąty naprzemianległe i odpowiadające
Pojęcia: pary kątów
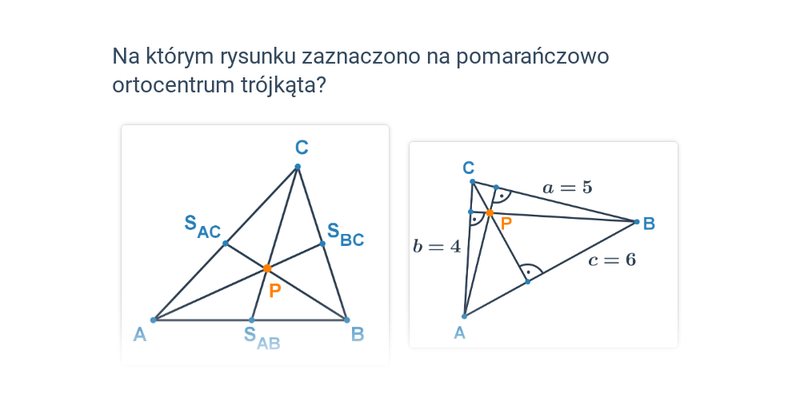
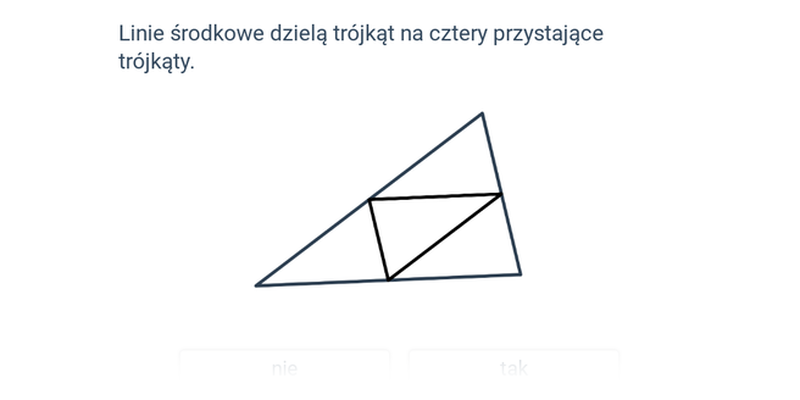
Pojęcia związane z trójkątem
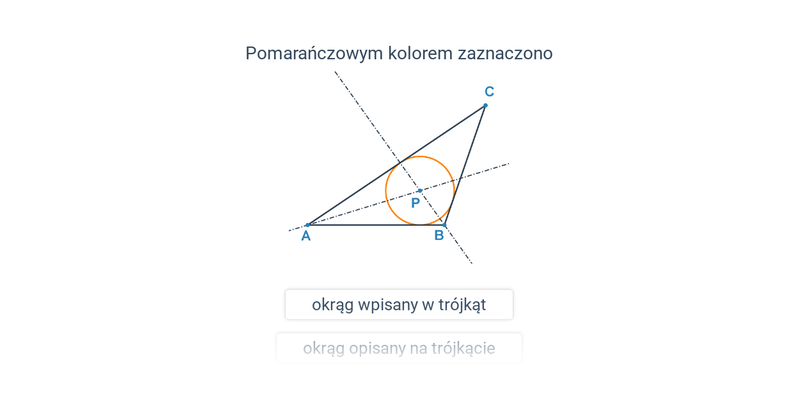
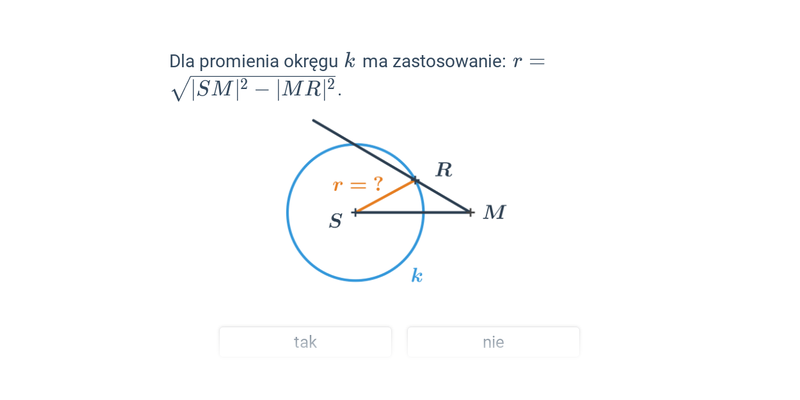
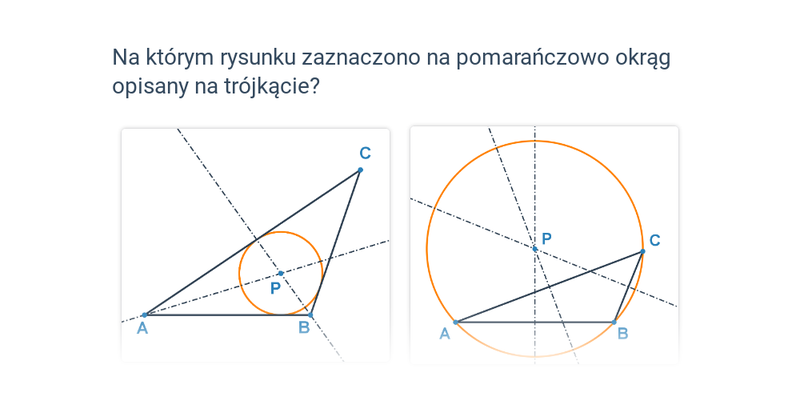
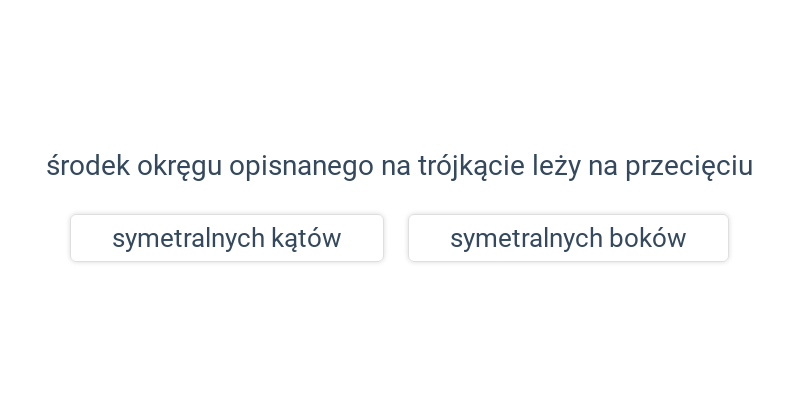
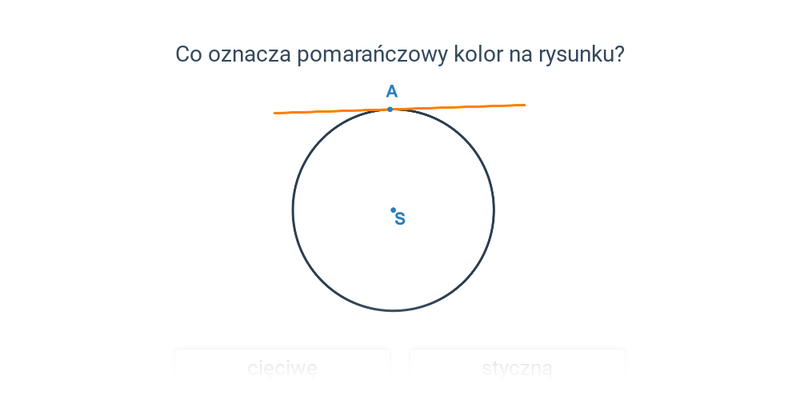
Pojęcia związane z okręgiem
Figury płaskie
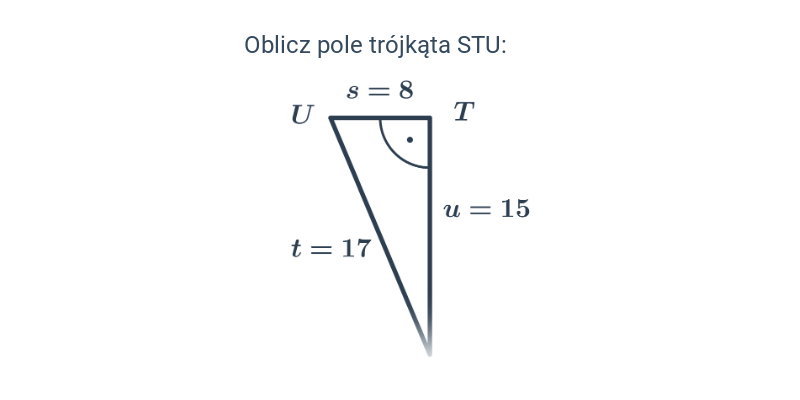
Trójkąt
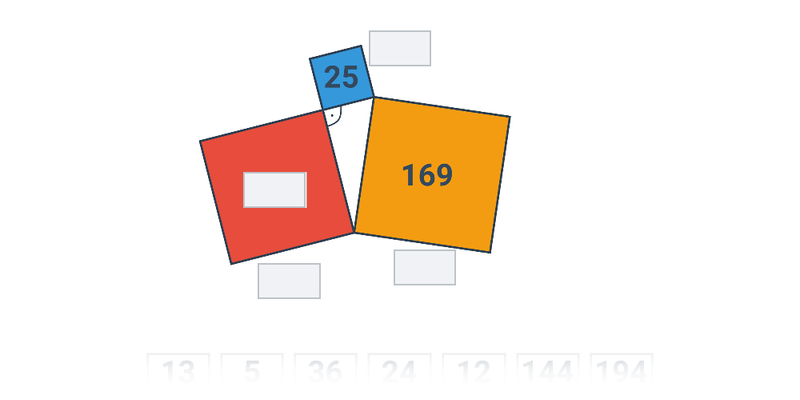
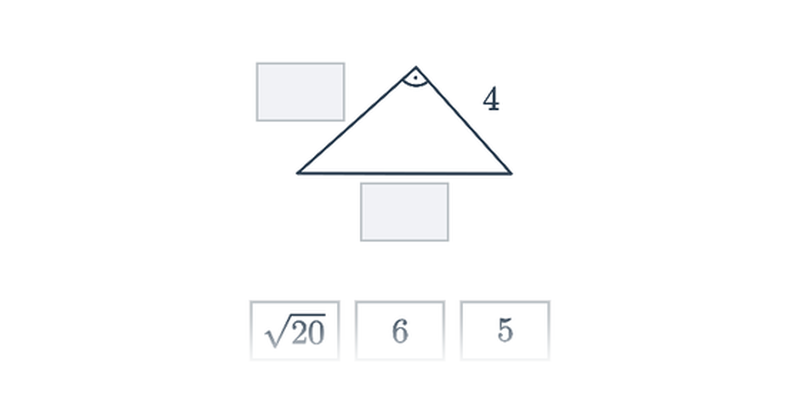
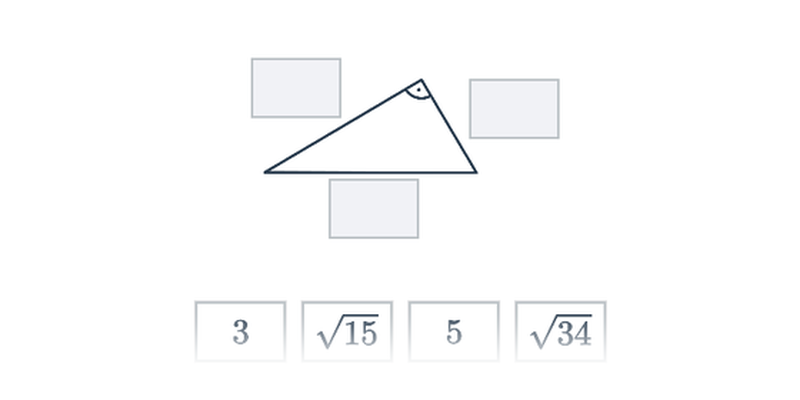
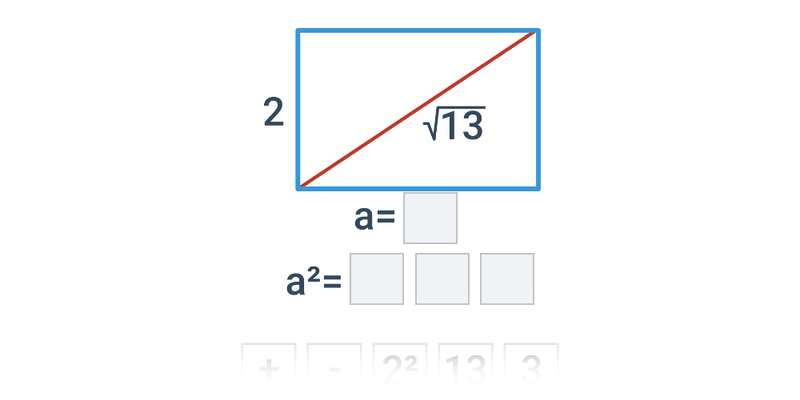
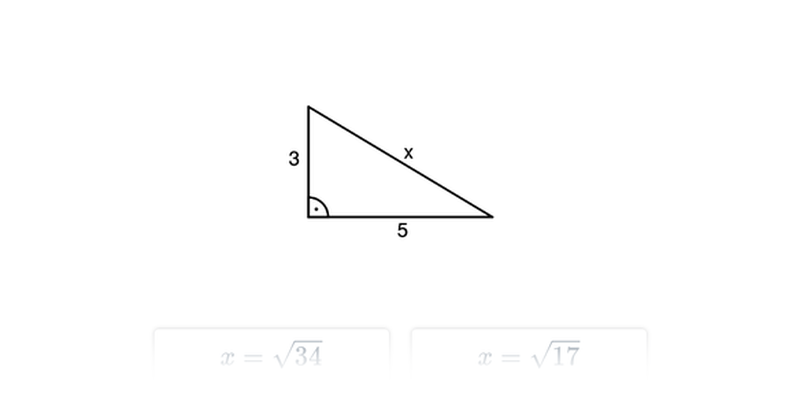
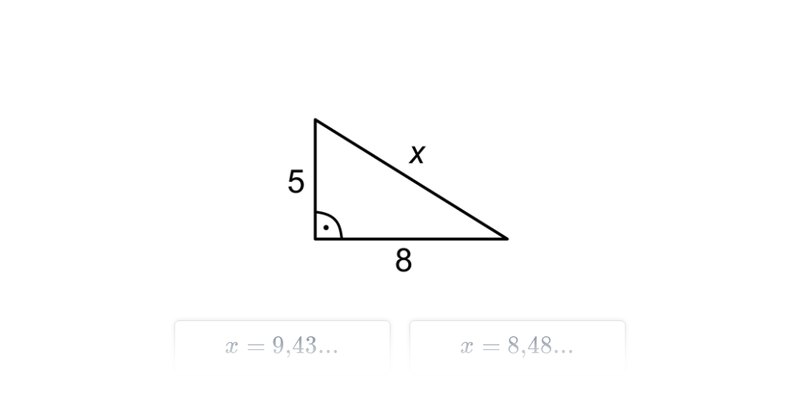
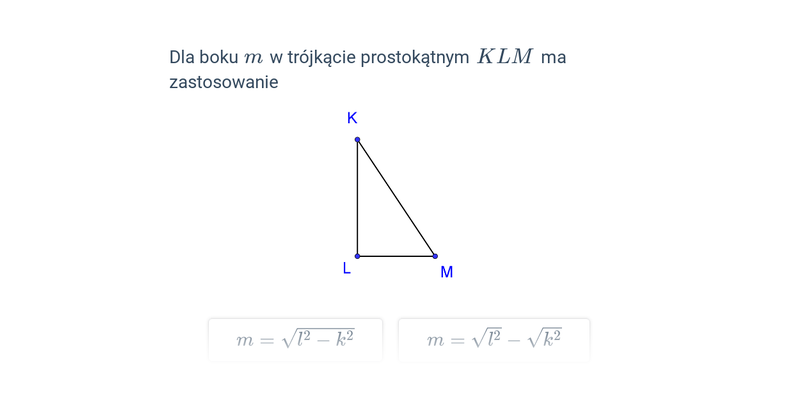
Twierdzenie Pitagorasa
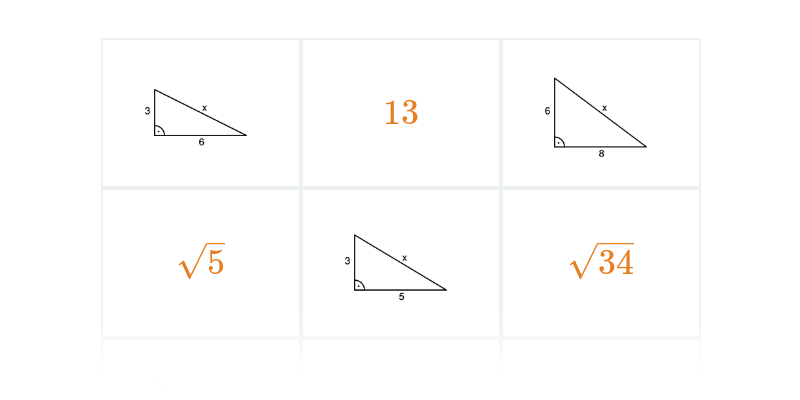
Twierdzenie Pitagorasa: podstawy
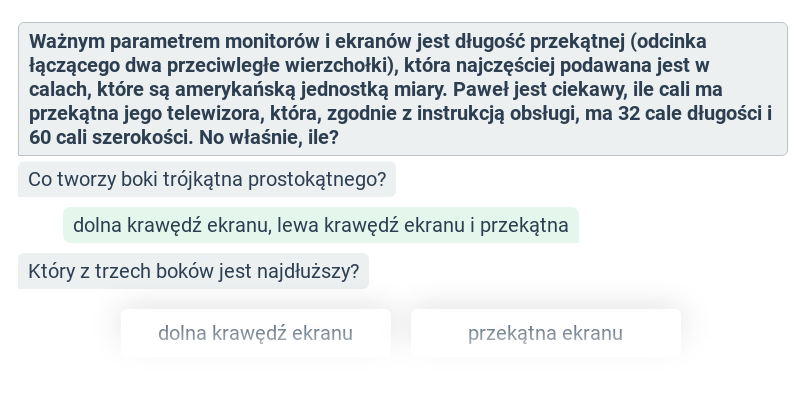
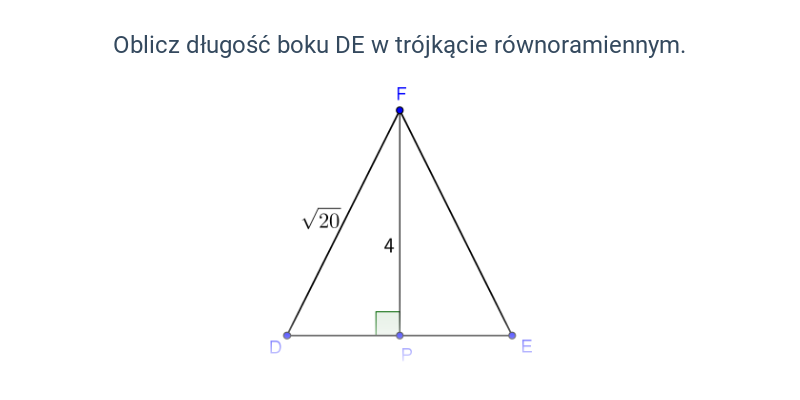
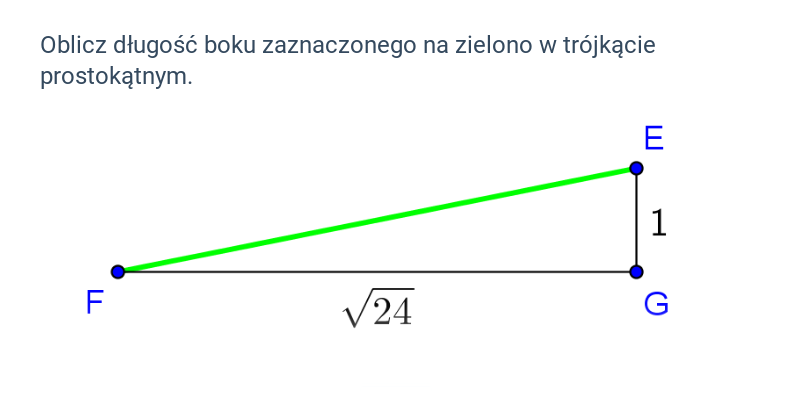
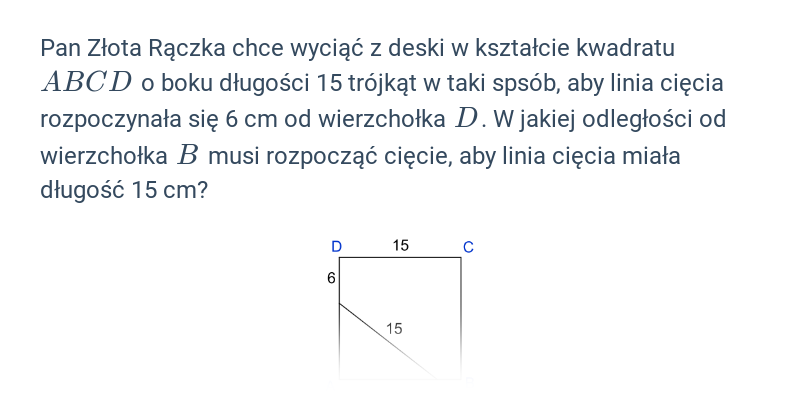
Twierdzenie Pitagorasa: zastosowanie

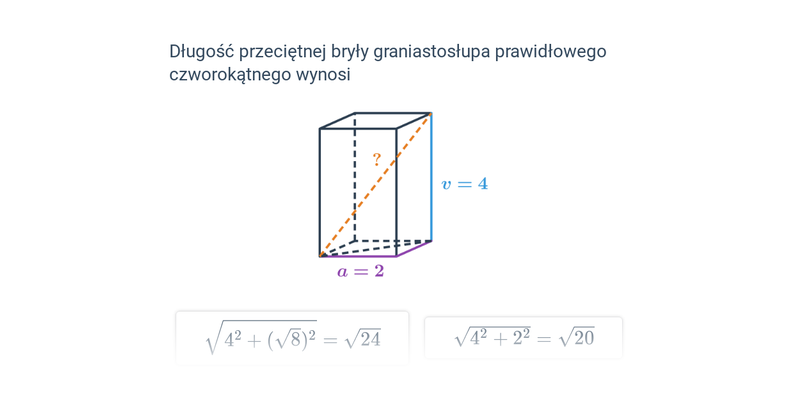
Twierdzenie Pitagorasa: zastosowanie w 3D
Trójkąt: miks przykładów
Kwadrat i prostokąt

Właściwości kwadratu i prostokąta
Koło i okrąg

Bryły
Sześcian i prostopadłościan
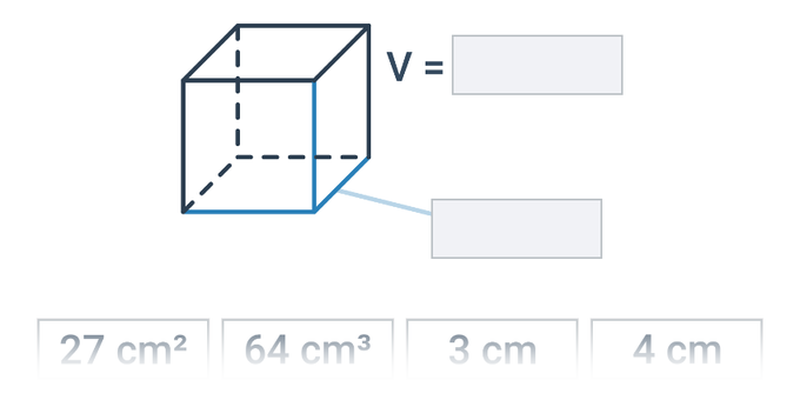
Sześcian, prostopadłościan: pojęcia i wzory
Walec
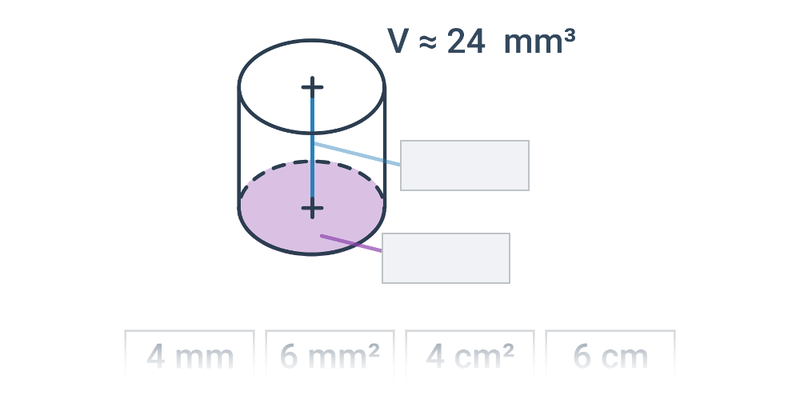
Walec: pojęcia i wzory
Kula

Kula: pojęcia i wzory
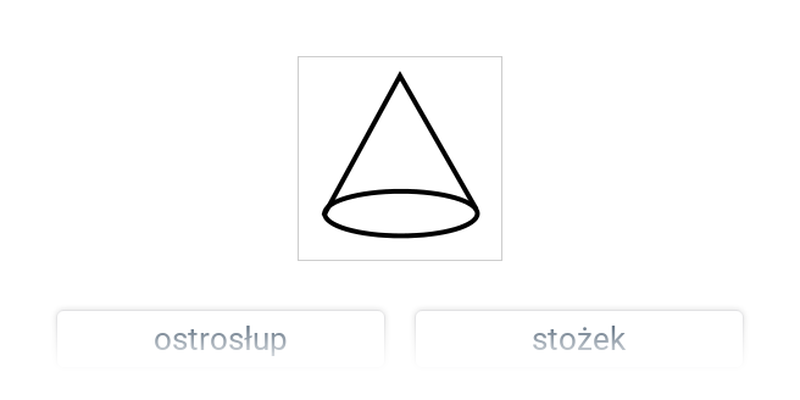
Stożek
Stożek: pojęcia i wzory
Pole powierzchni i obwód
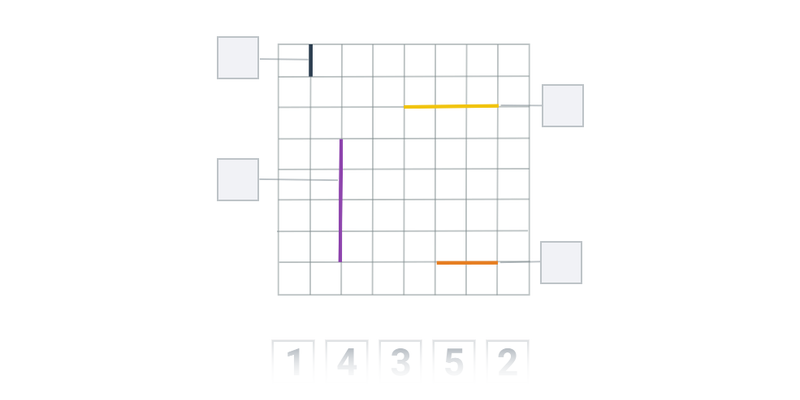
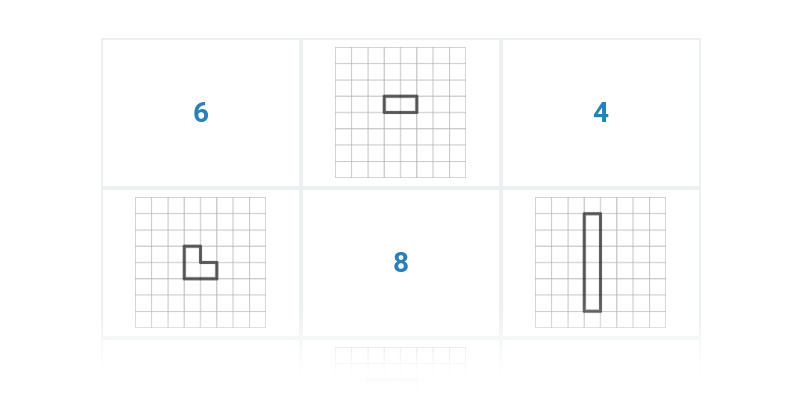
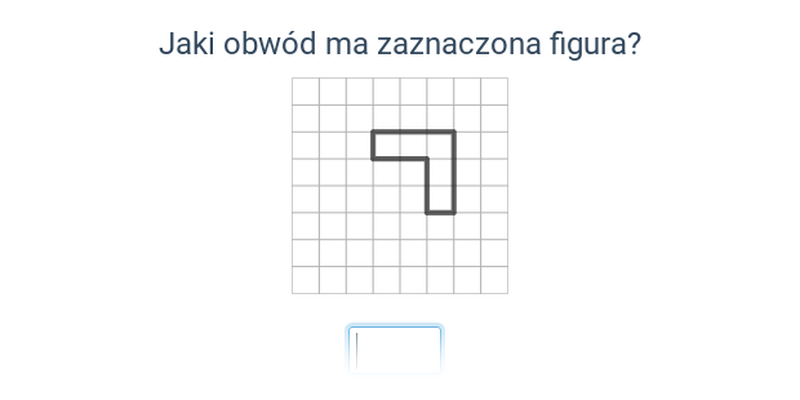
Długość i obwód (na kratce)
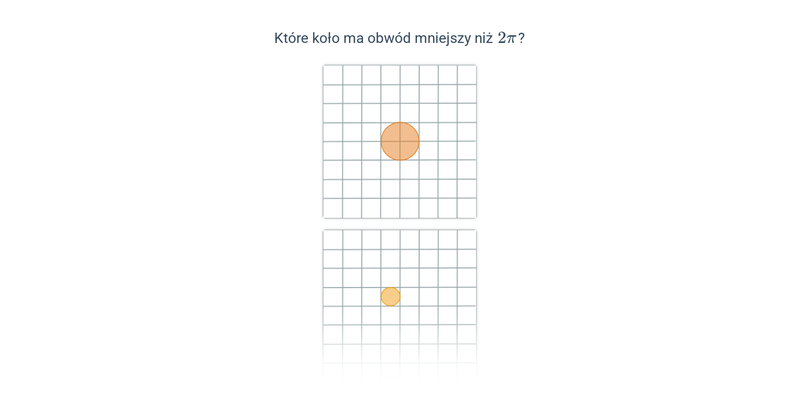
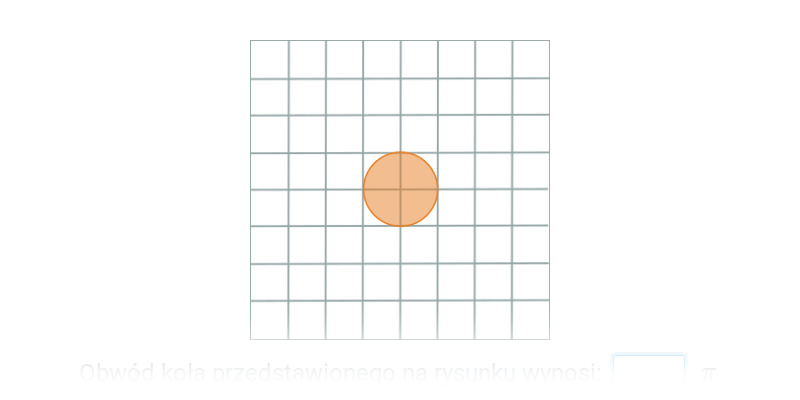
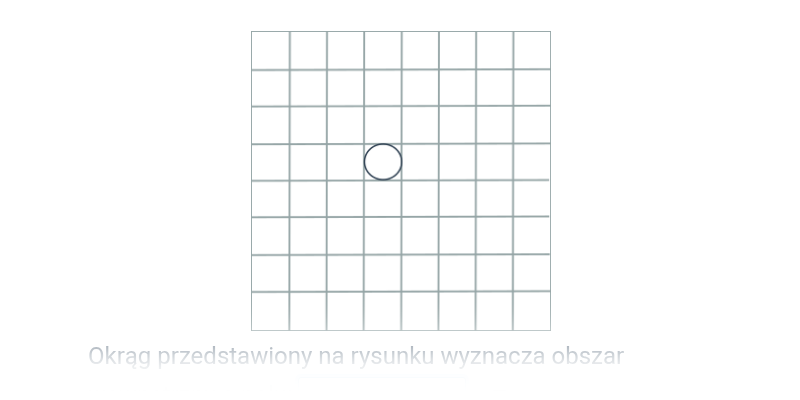
Obwód koła, długość okręgu (na kratce)
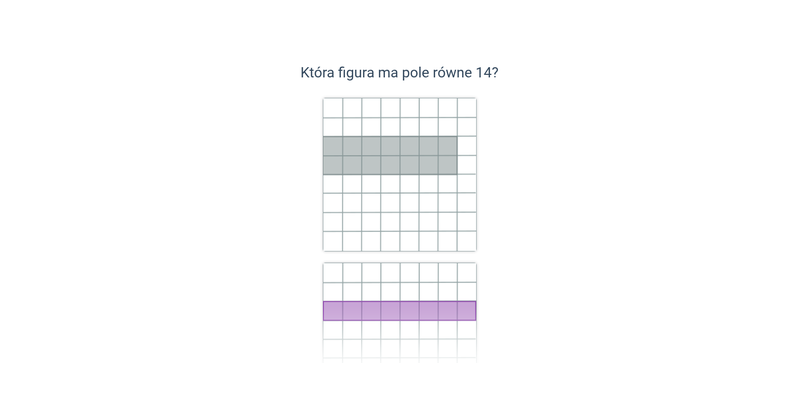
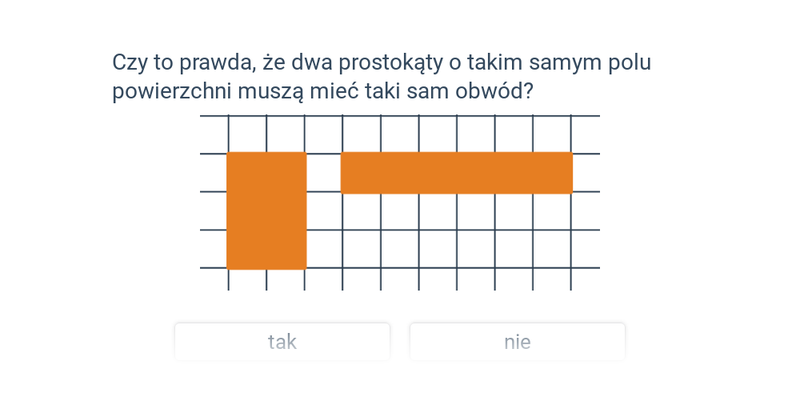
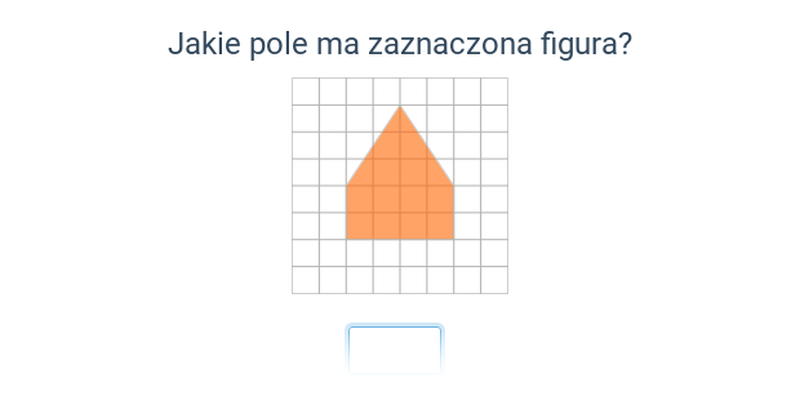
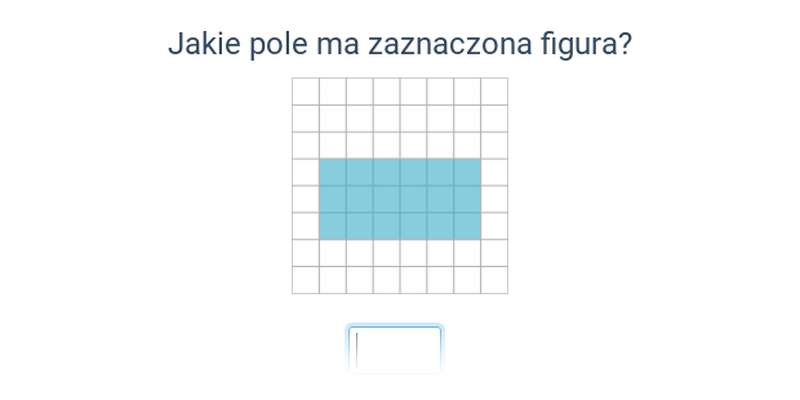
Pole powierzchni (na kratce)
Pole kwadratu i prostokąta (na kratce)
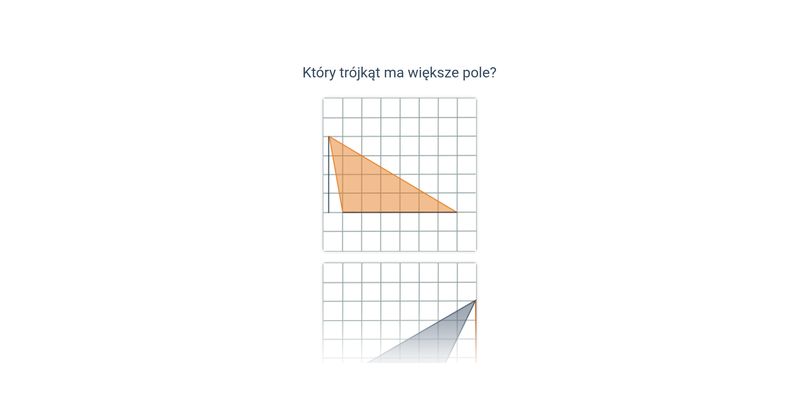
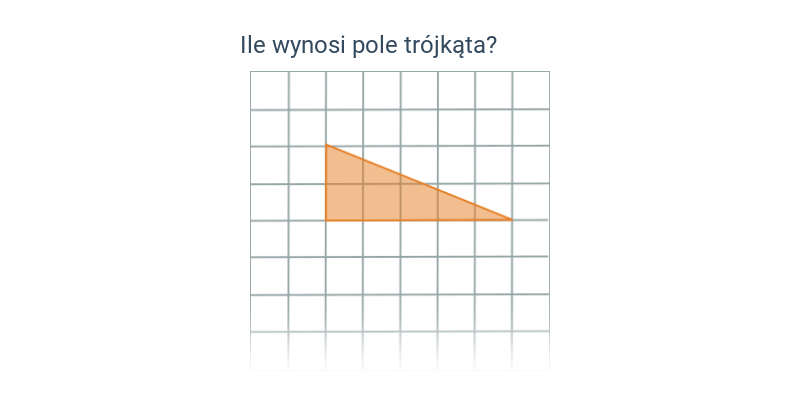
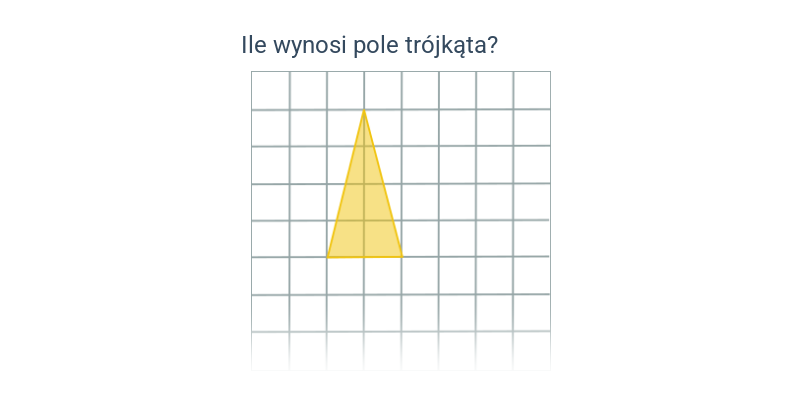
Pole trójkąta (na kratce)
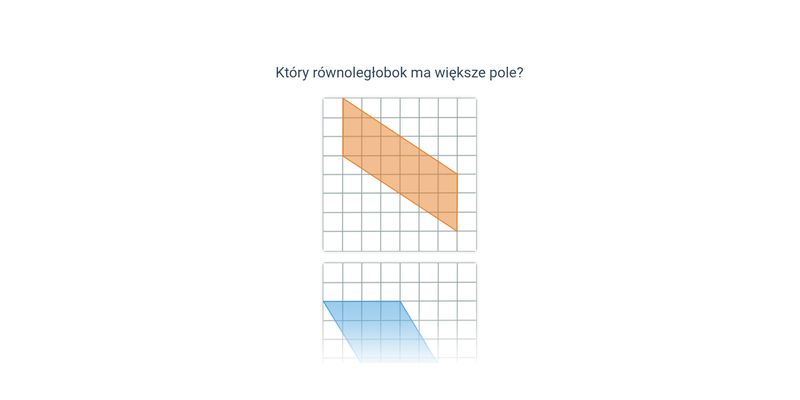
Pole równoległoboku (na kratce)
Pole trapezu (na kratce)
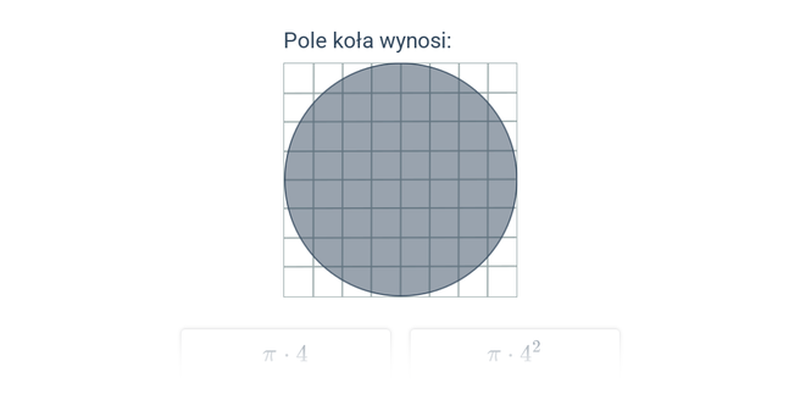
Pole koła (na kratce)
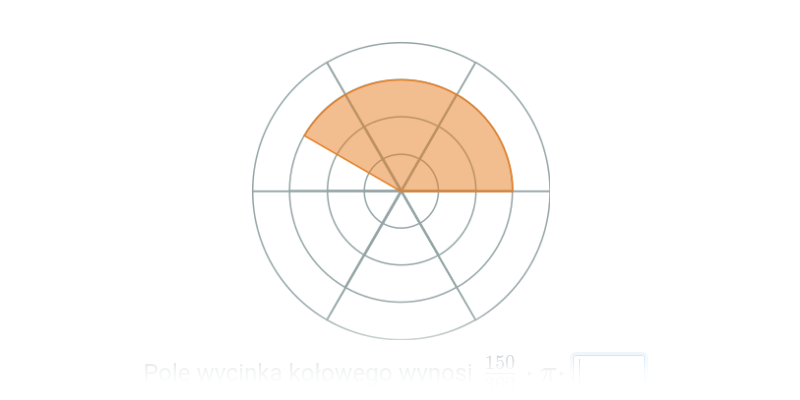
Pole wycinka kołowego (na kratce)
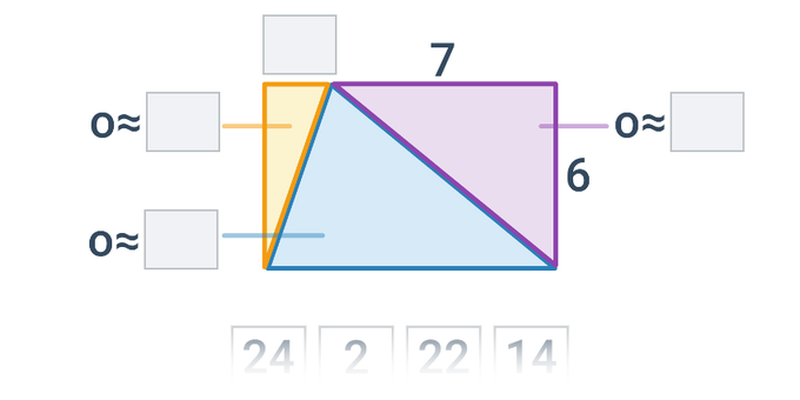
Długość i obwód
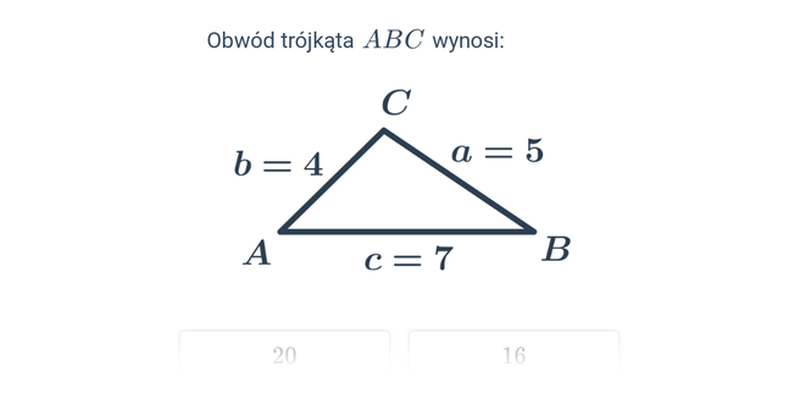
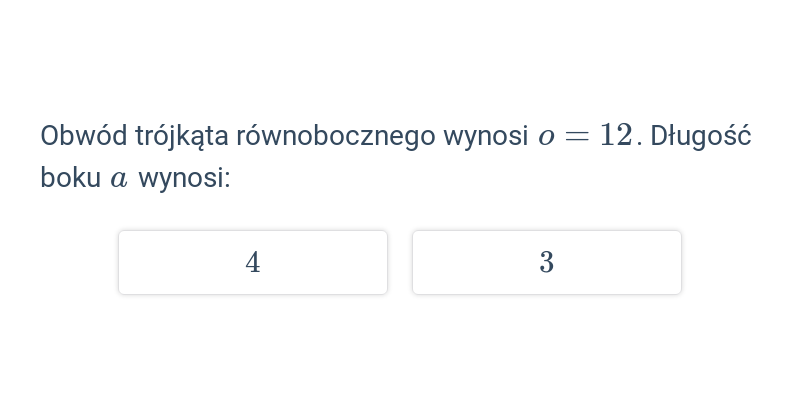
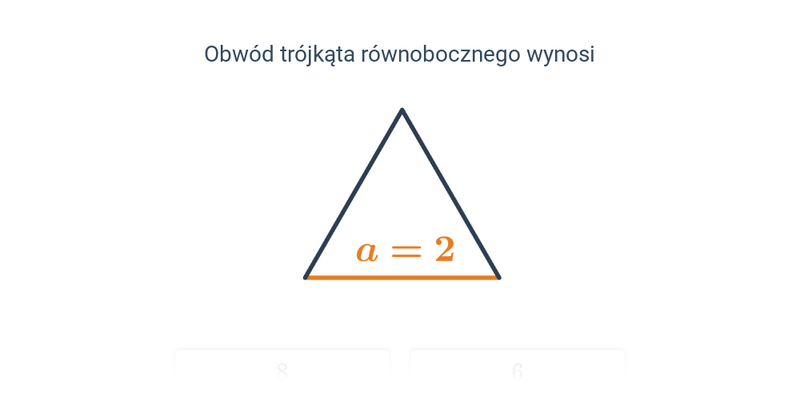
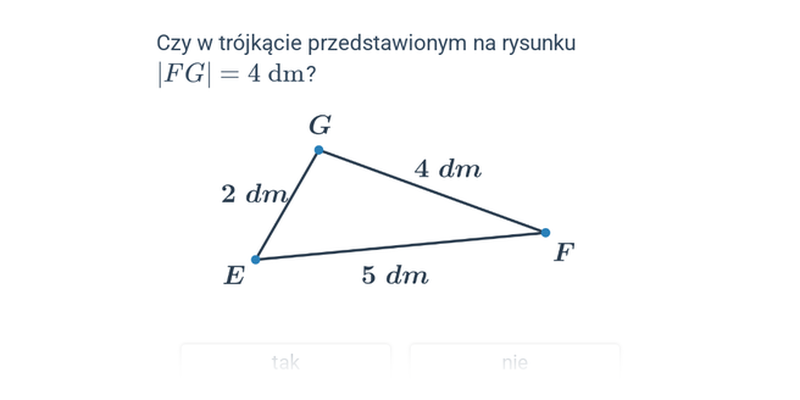
Obwód trójkąta

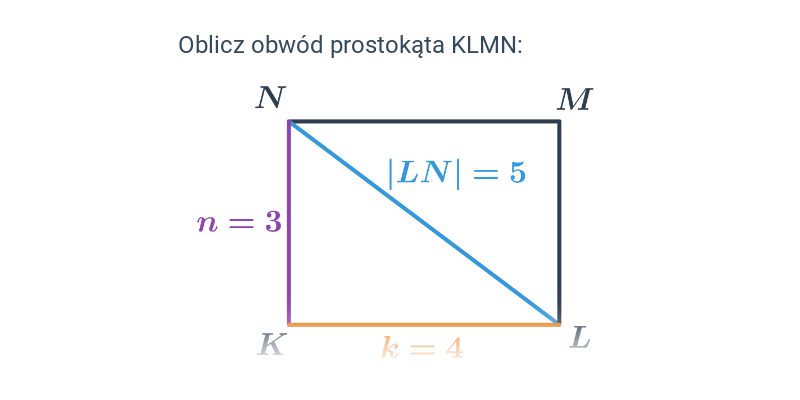
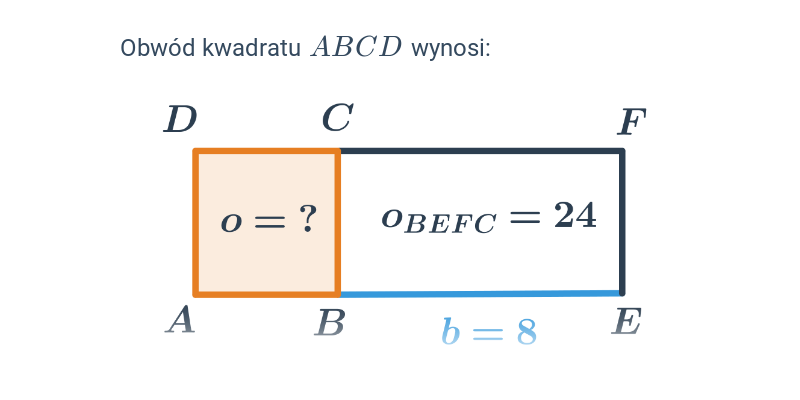
Obwód kwadratu i prostokąta

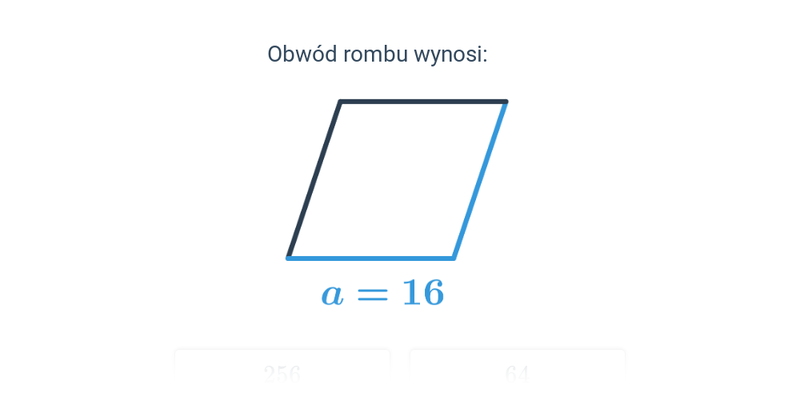
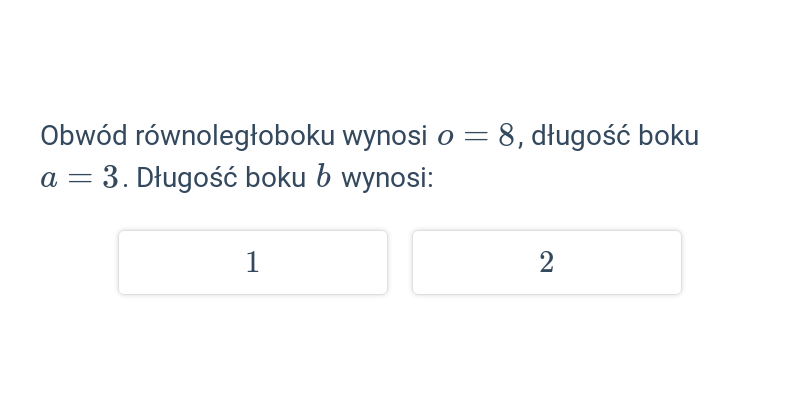
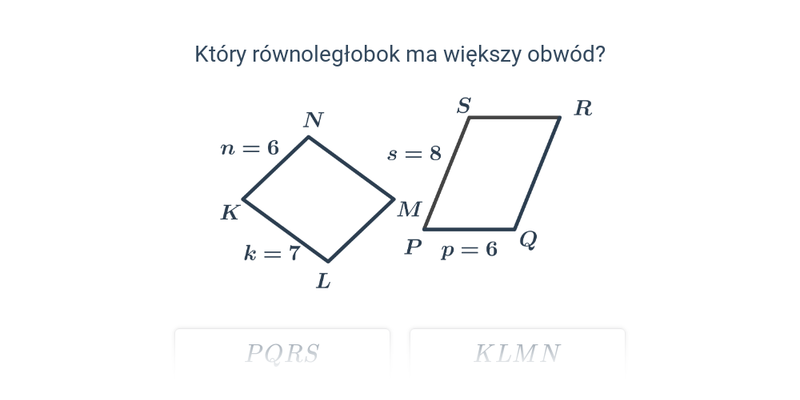
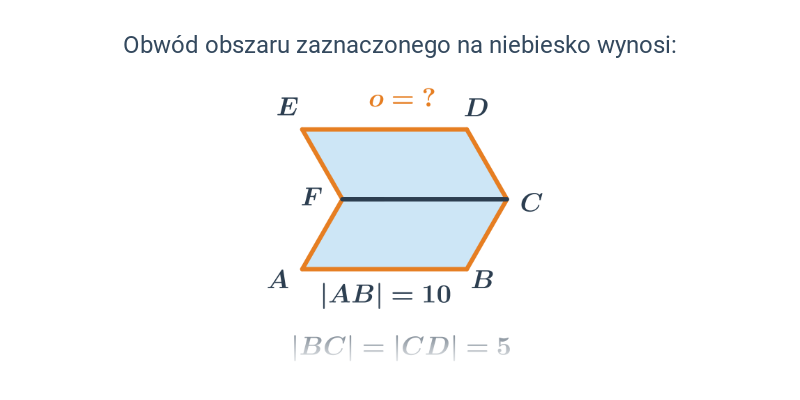
Obwód równoległoboku

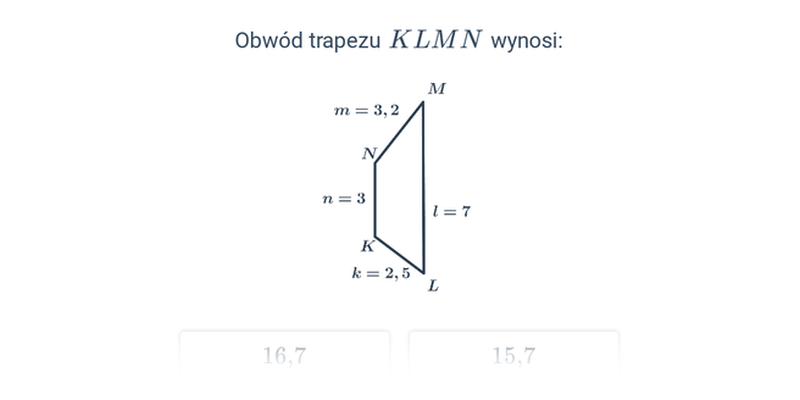
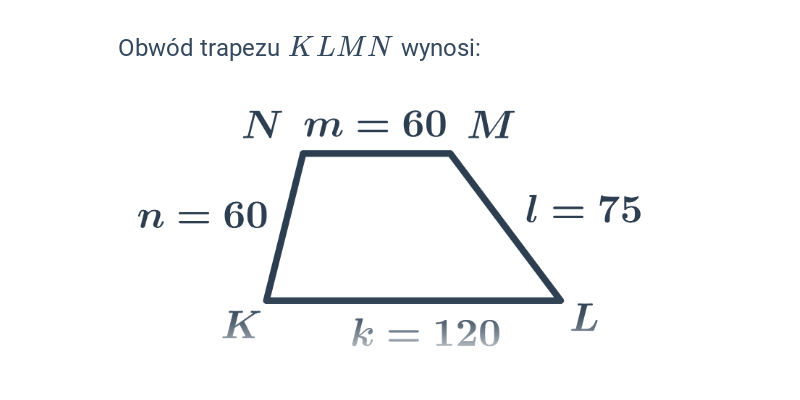
Obwód trapezu

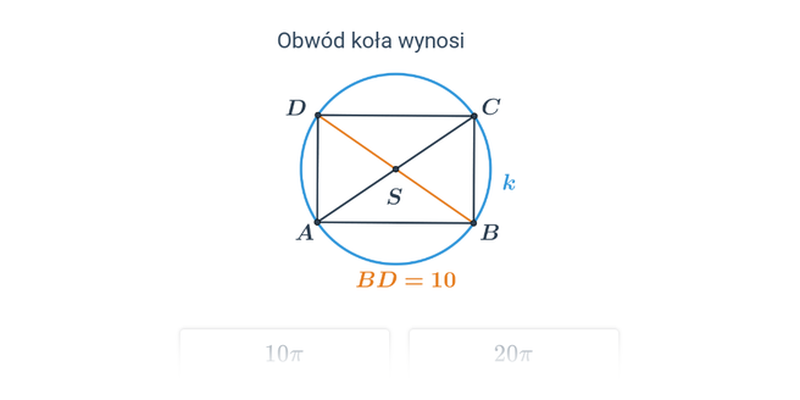
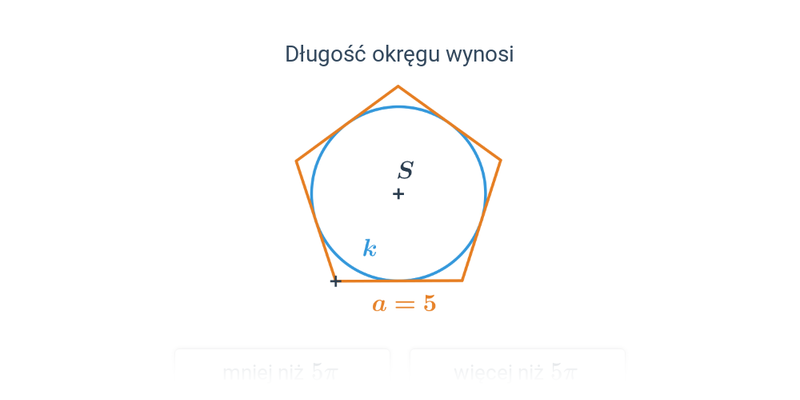
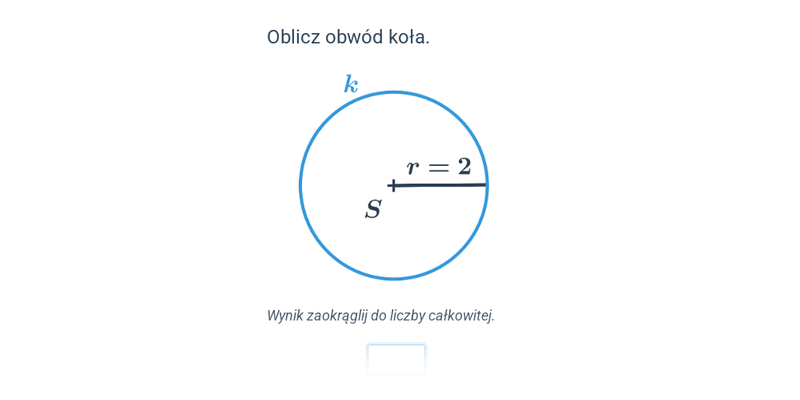
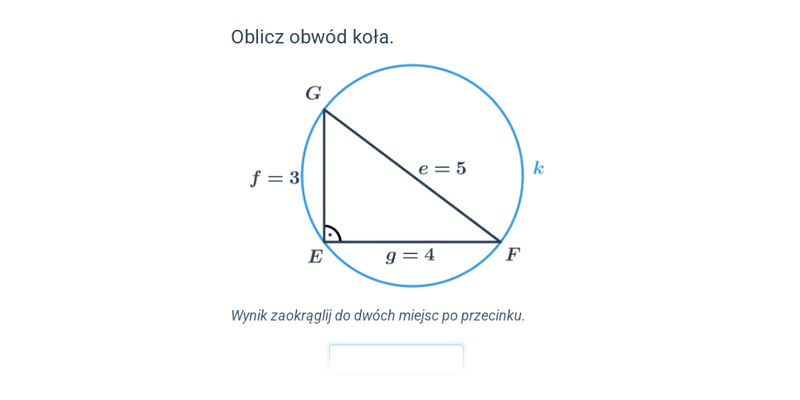
Obwód koła, długość okręgu

Długość łuku

Obwód: miks przykładów

Obwód: kwadrat, prostokąt, trójkąt
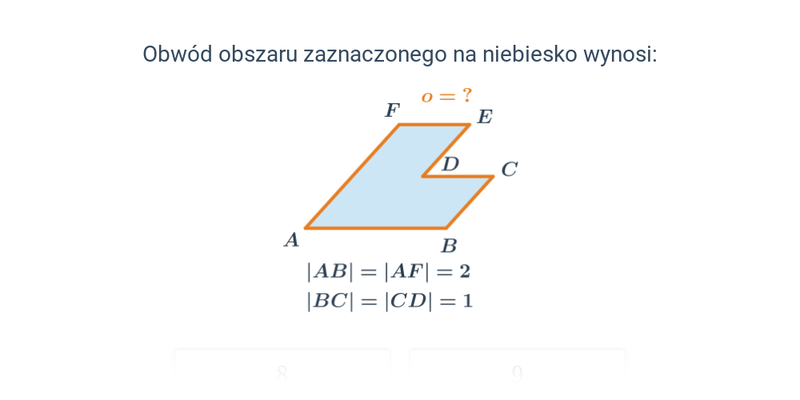
Obwód: równoległobok, trapez, czworokąt
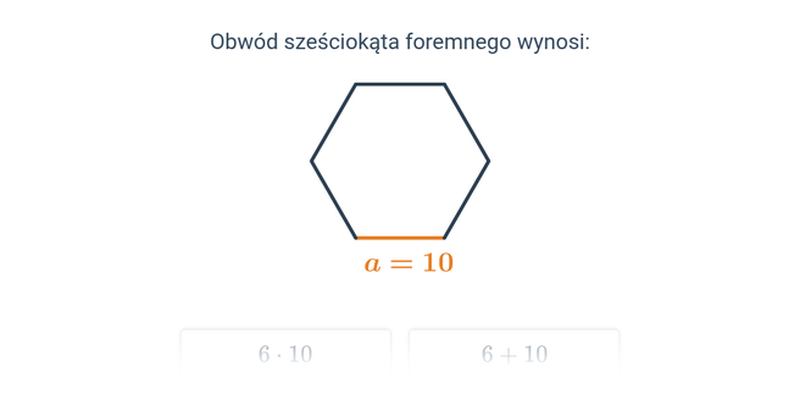
Obwód: wielokąty foremne
Pole powierzchni
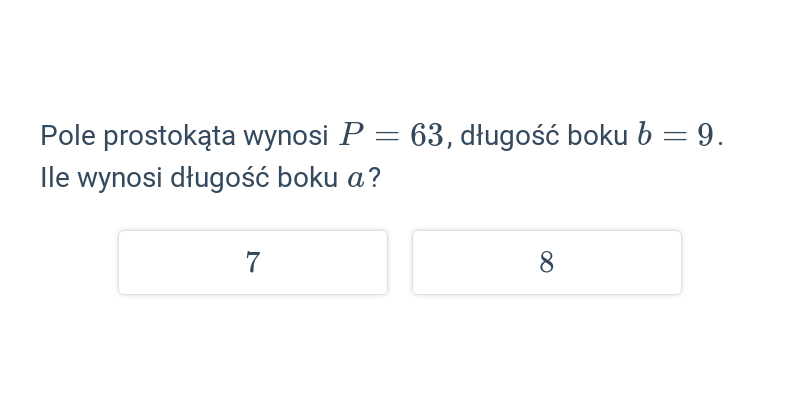
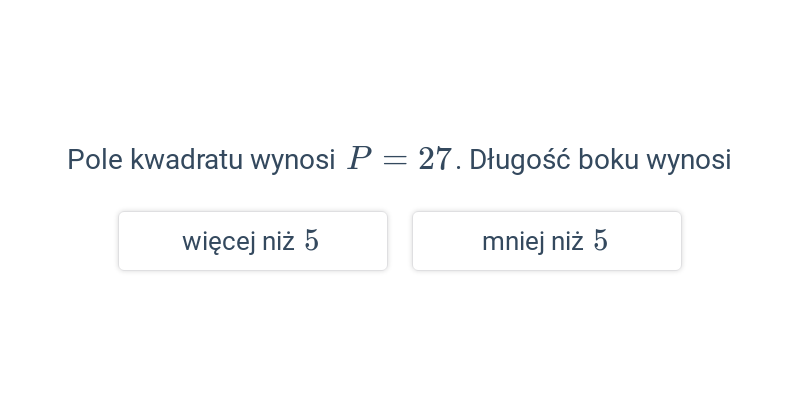
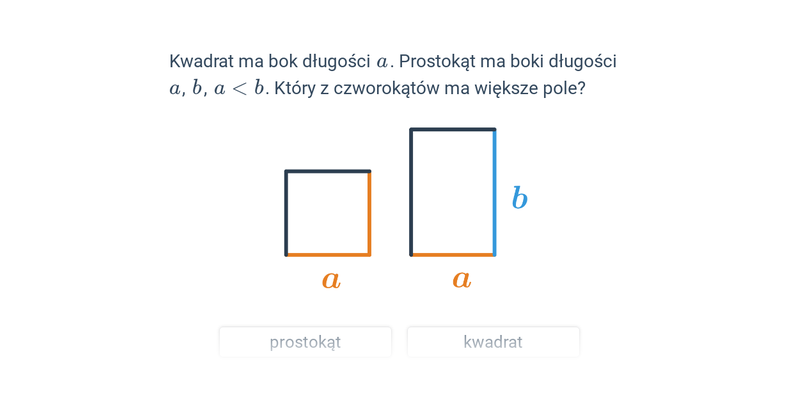
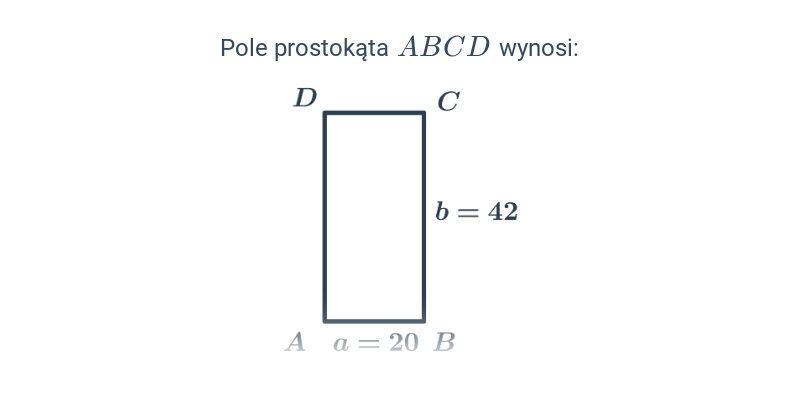
Pole kwadratu i prostokąta
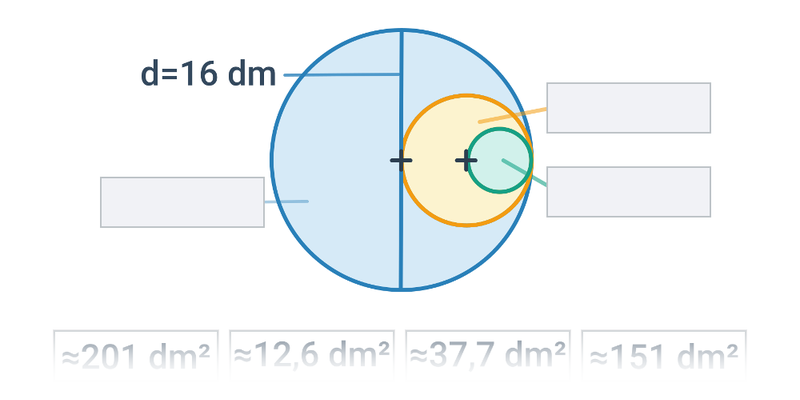
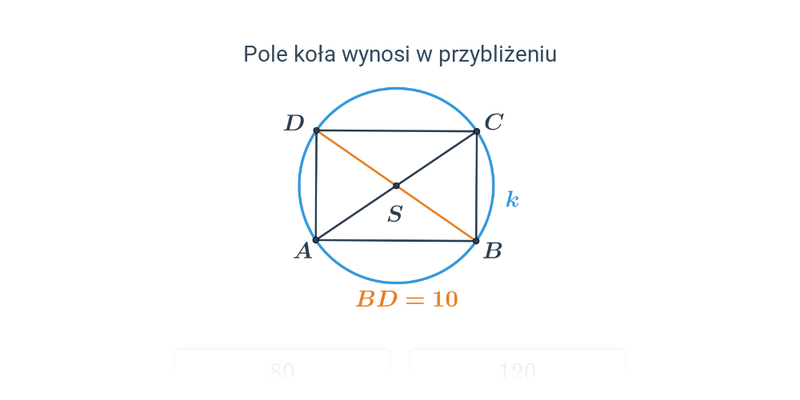
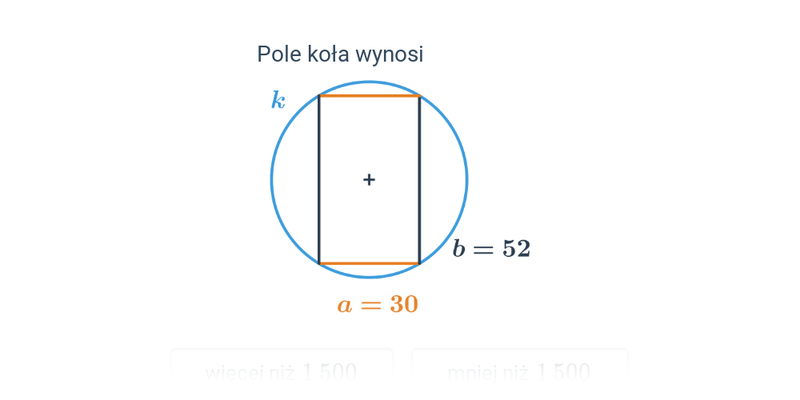
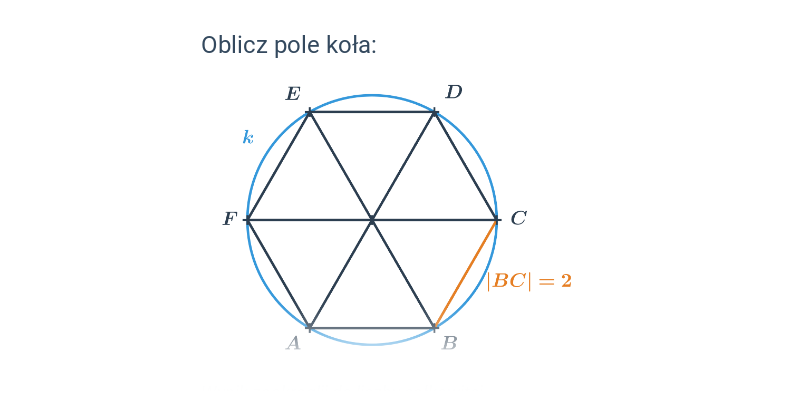
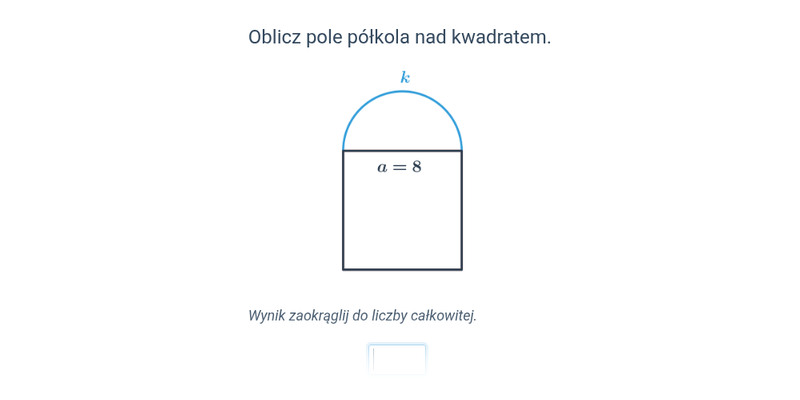
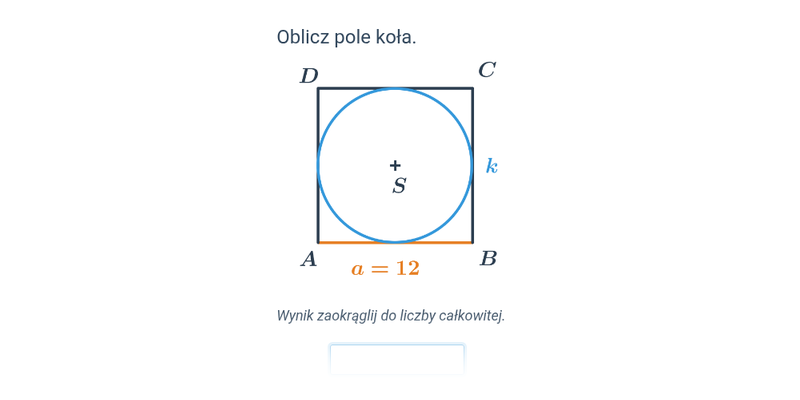
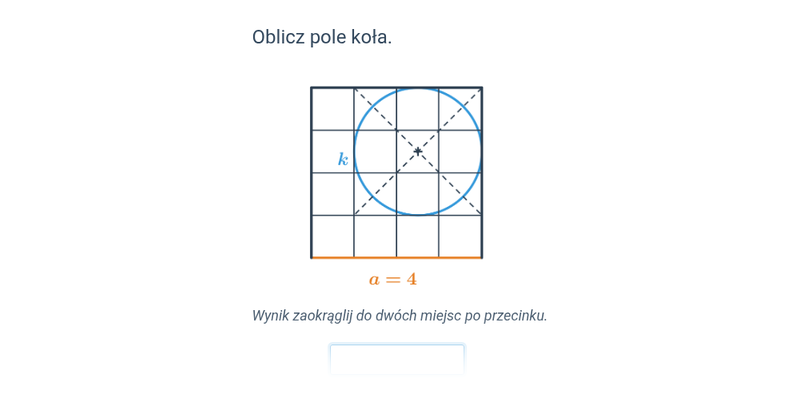
Pole koła

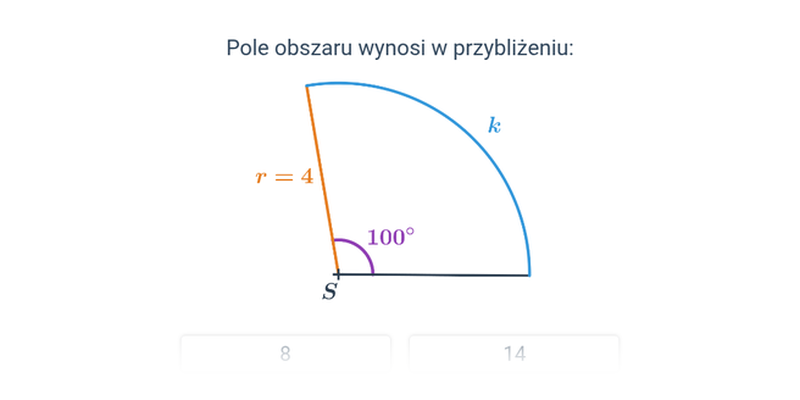
Pole wycinka kołowego
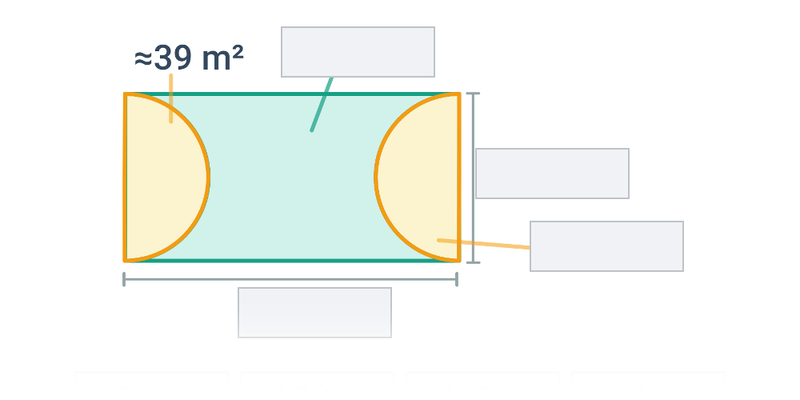
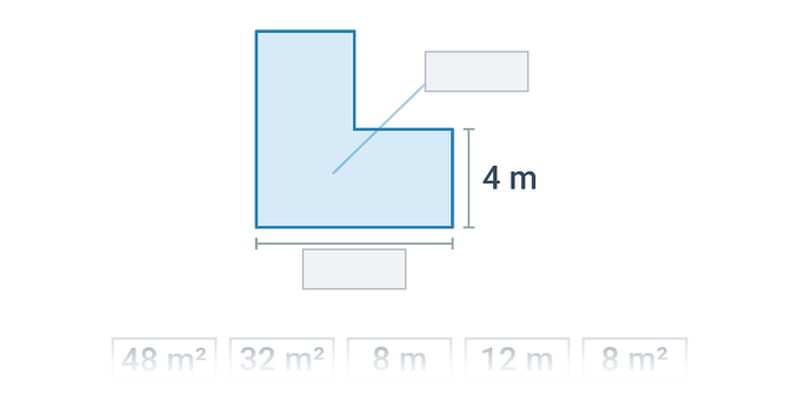
Pole: kombinacje figur
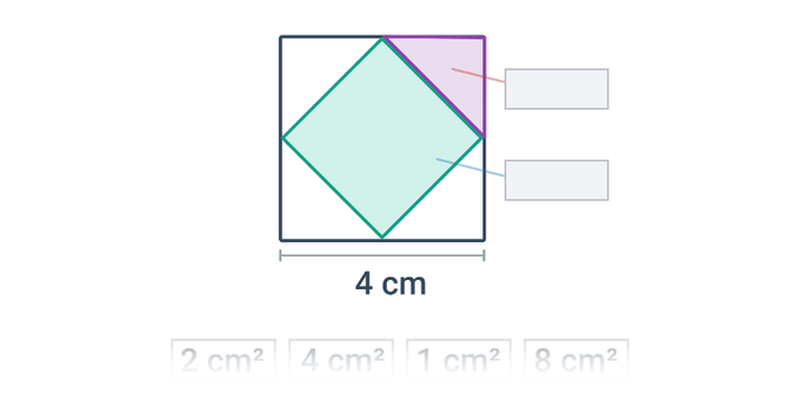
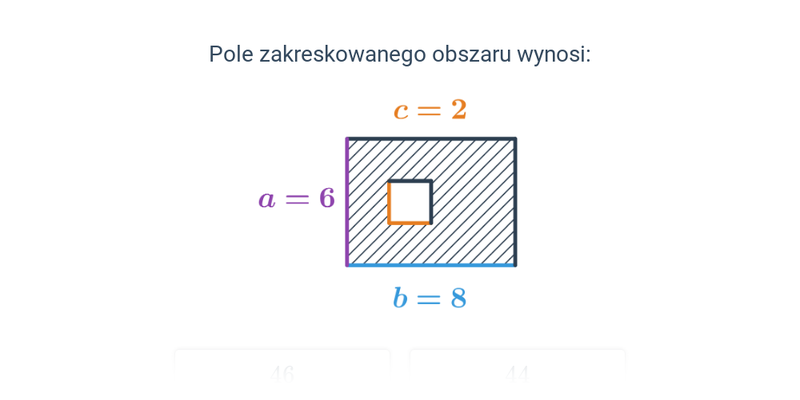
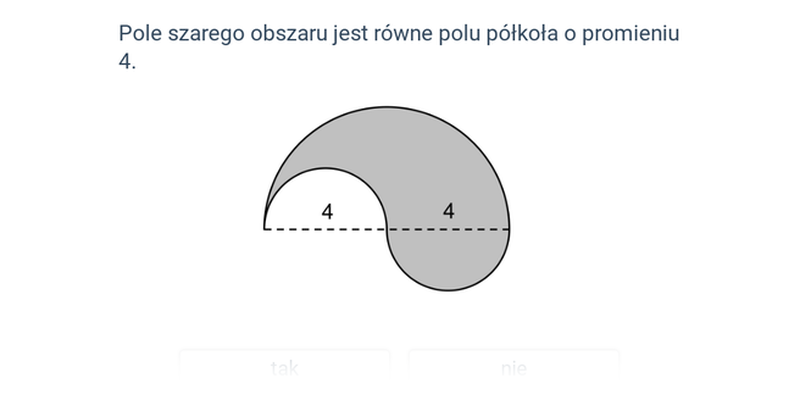
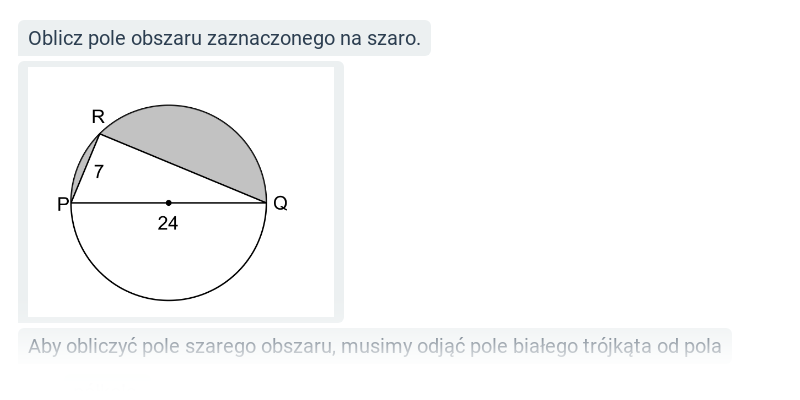
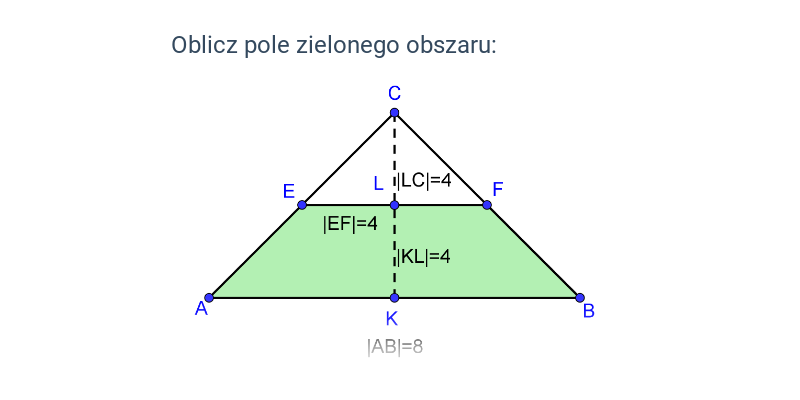
Pole zacieniowanego obszaru
Pole powierzchni: miks przykładów
Pole na kratce: trójkąt, równoległobok, trapez
Pole, obwód: miks przykładów
Pole, obwód: koło i wycinek kołowy (różne)
Pole, obwód: wzory, zasady
Objętość i pole powierzchni całkowitej
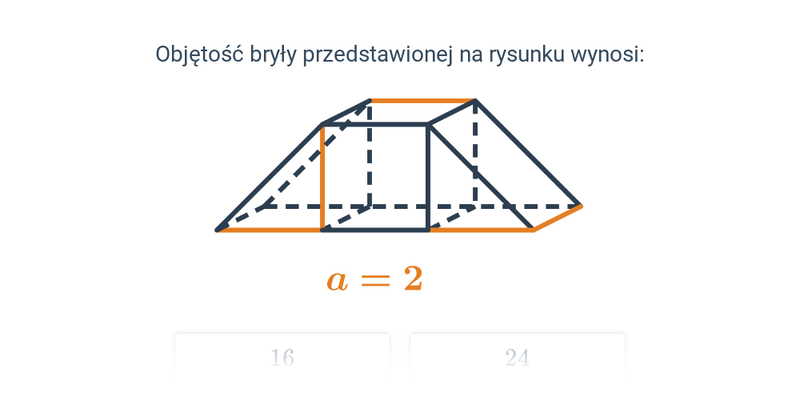
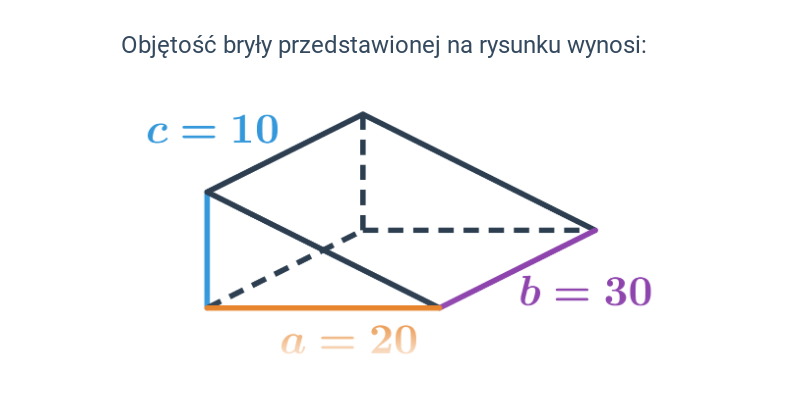
Objętość
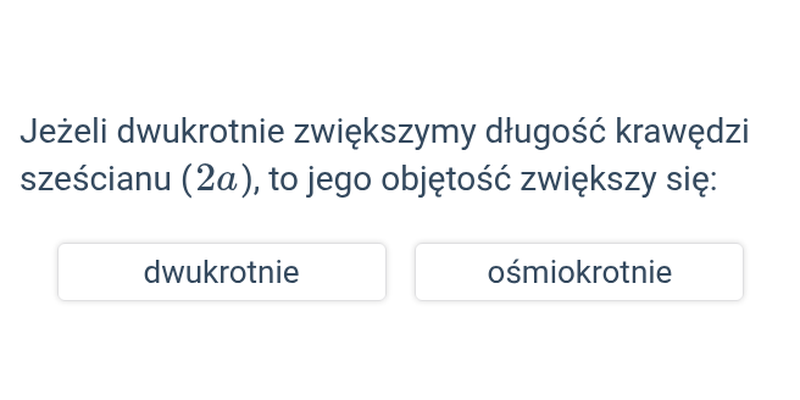
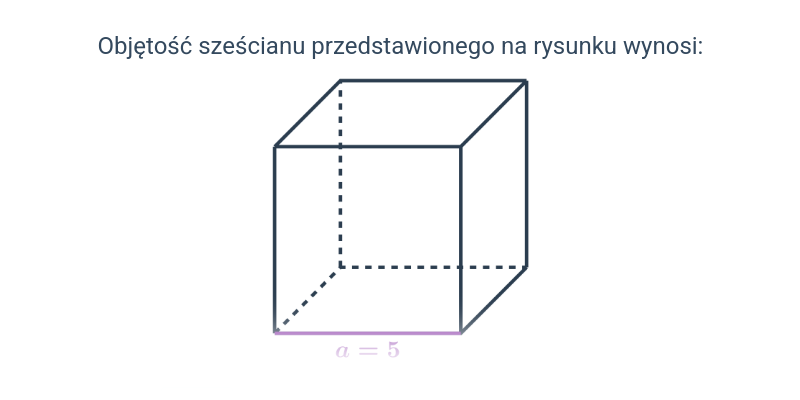
Objętość sześcianu i prostopadłościanu
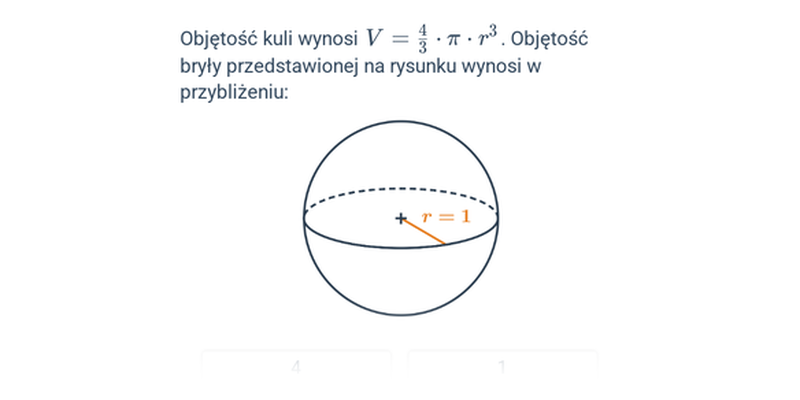
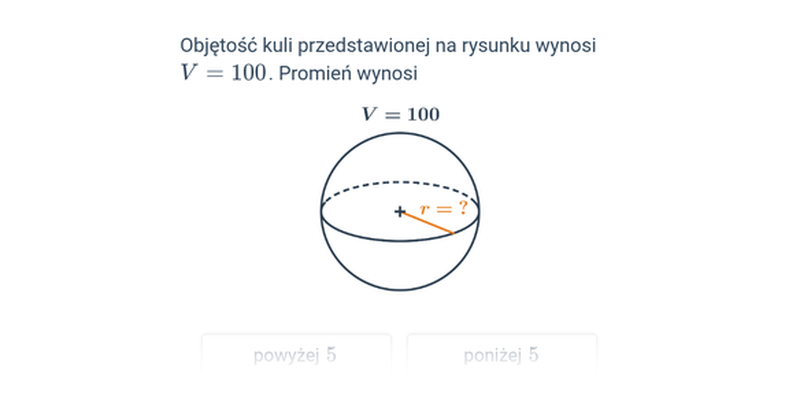
Objętość kuli
Pole powierzchni całkowitej
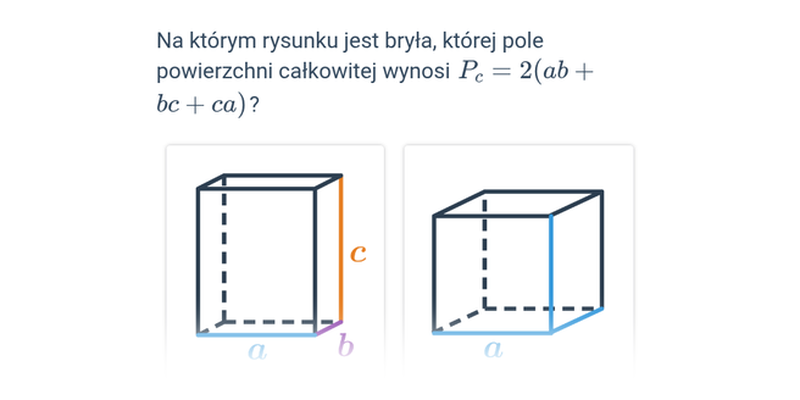
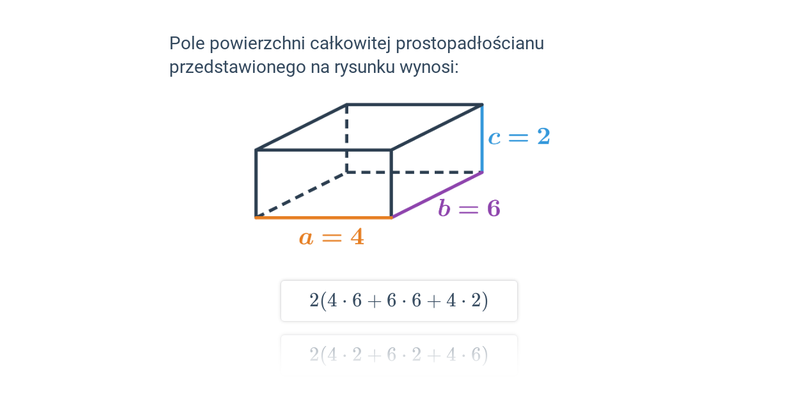
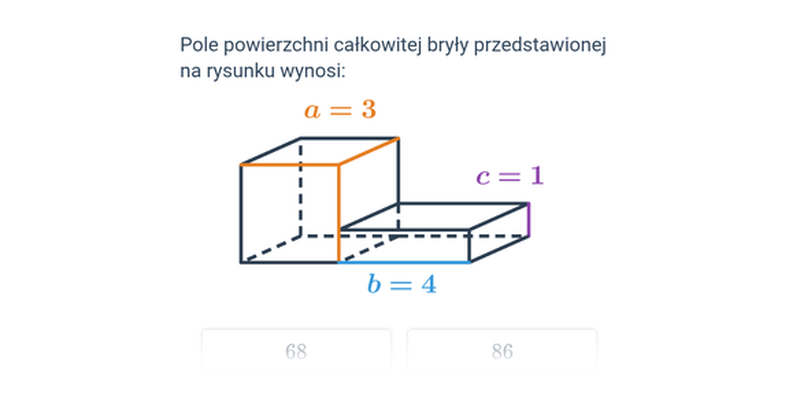
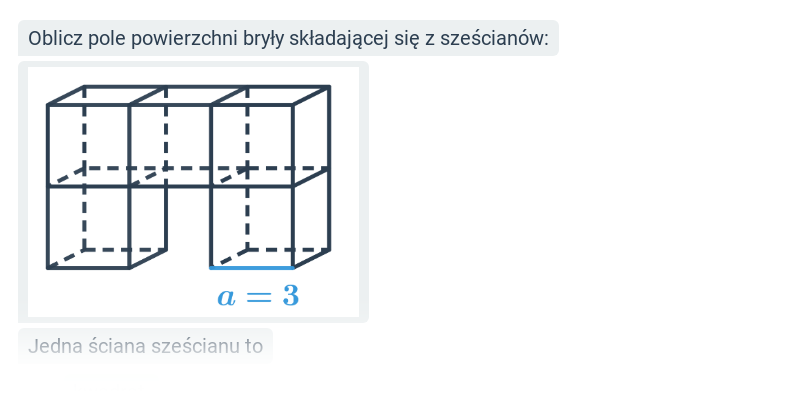
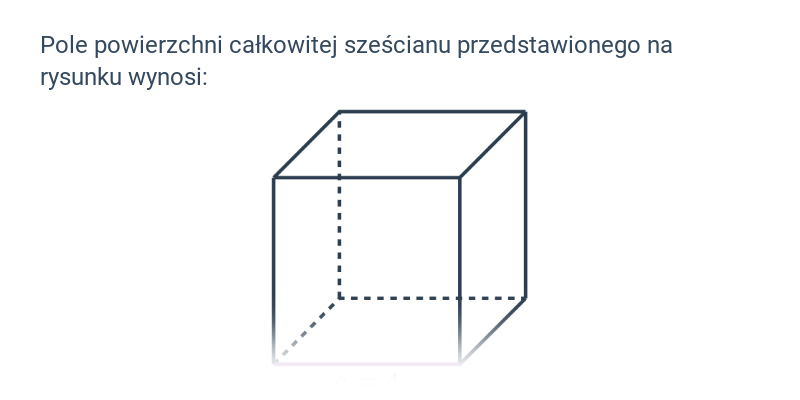
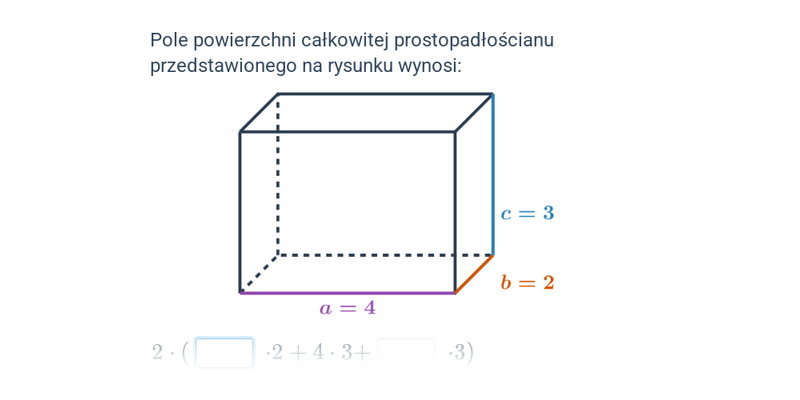
Pole powierzchni całkowitej sześcianu i prostopadłościanu
Pole powierzchni całkowitej kuli

Objętość, pole powierzchni całkowitej: miks przykładów
Objętość, pole: wzory, zasady
Kąty
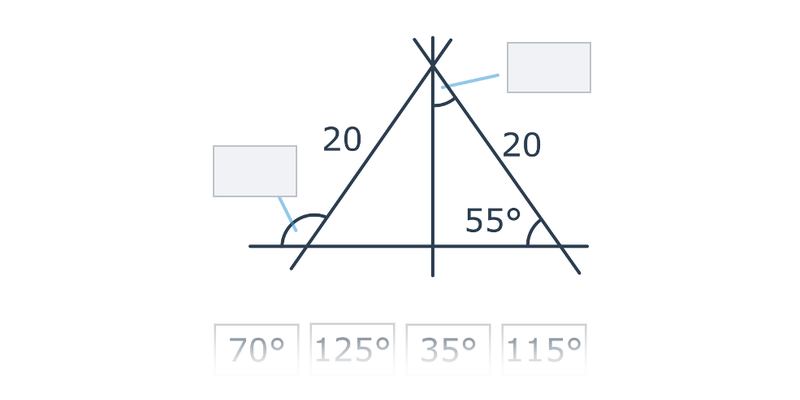
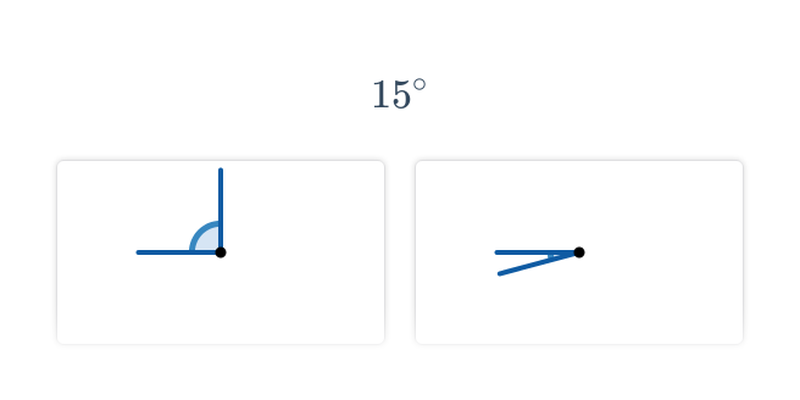
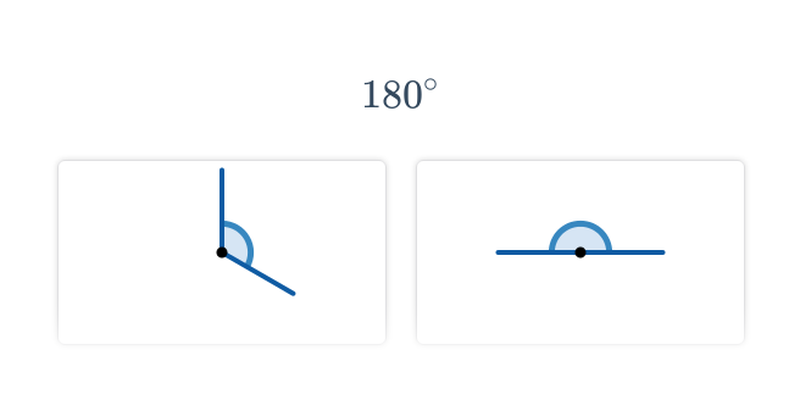
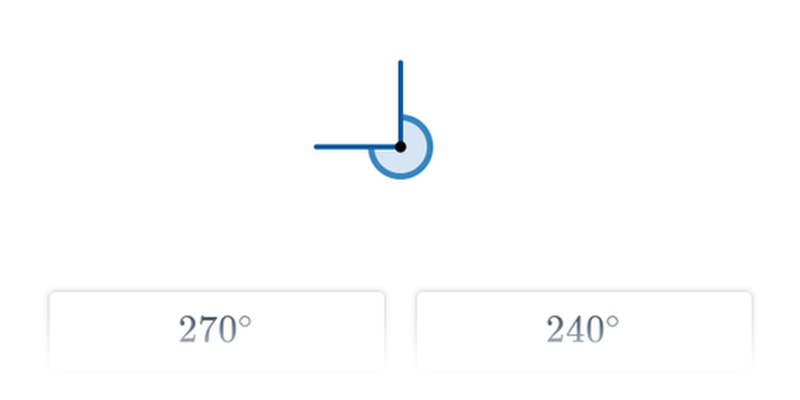
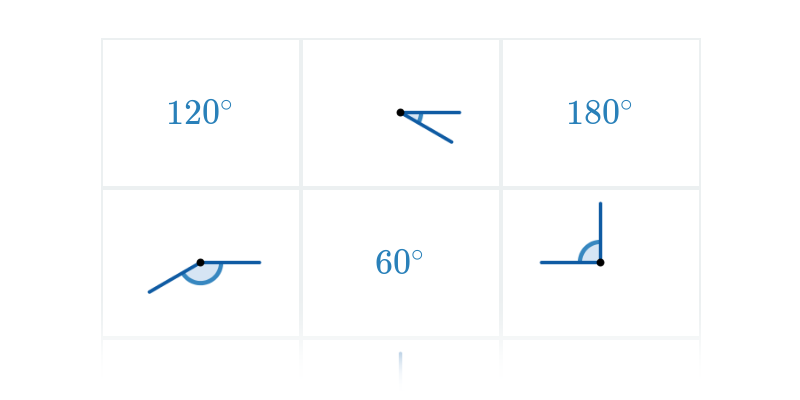
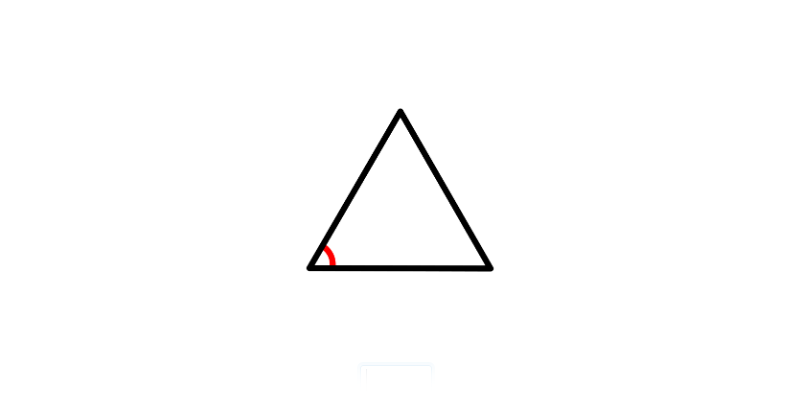
Szacowanie miary kąta

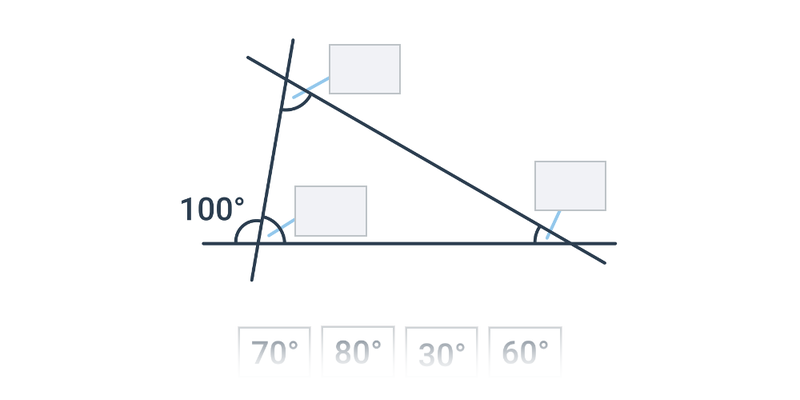
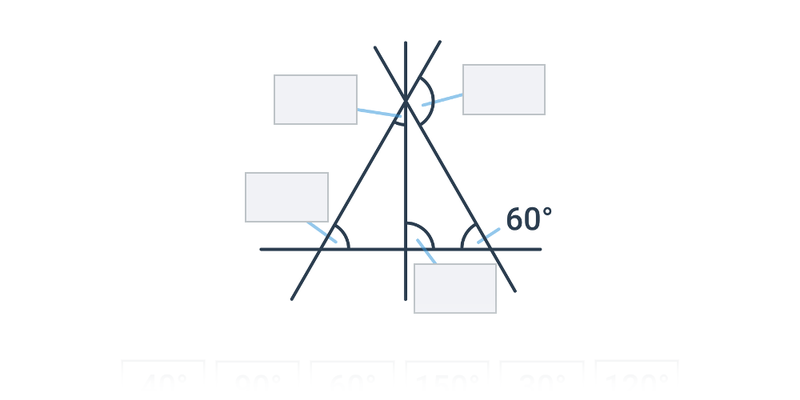
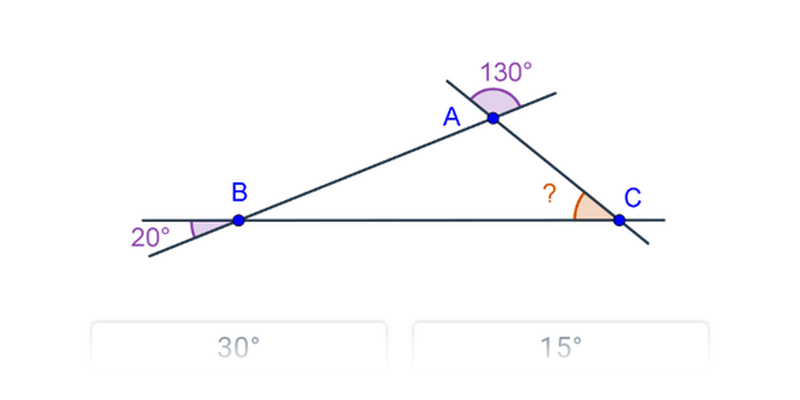
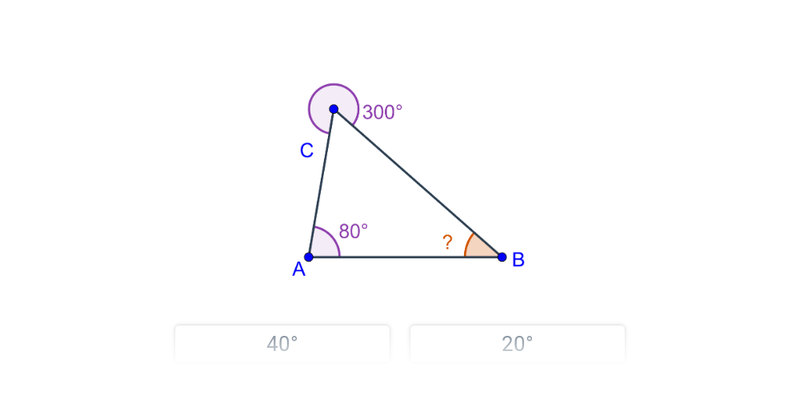
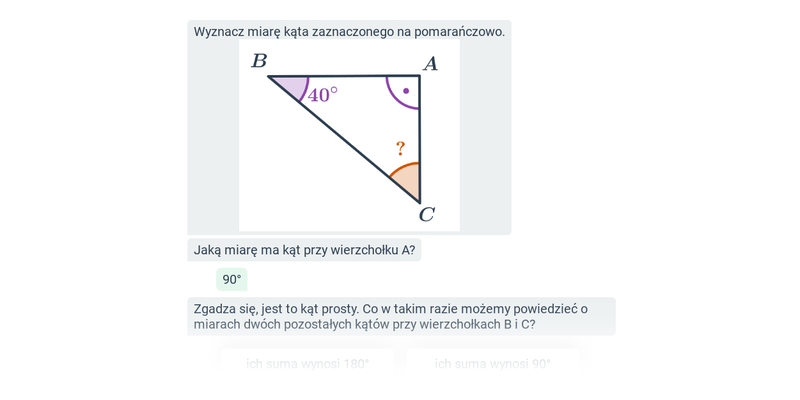
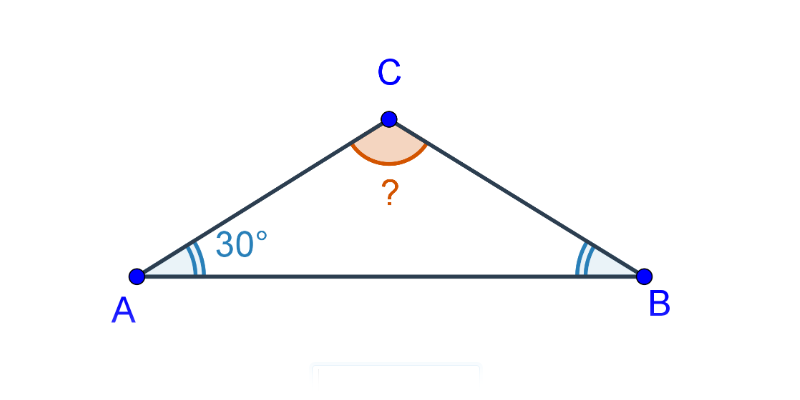
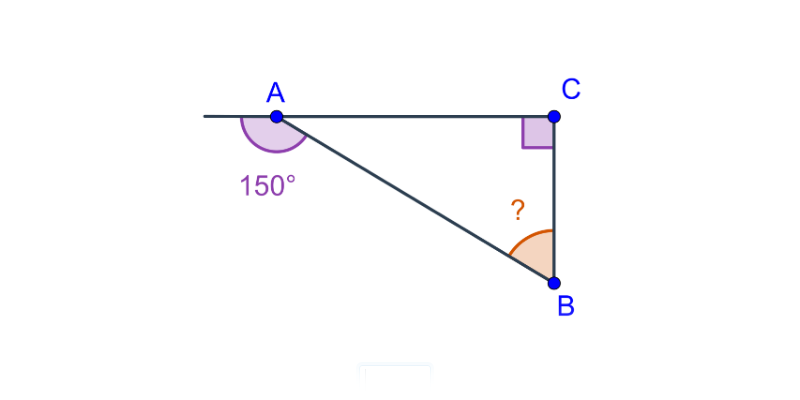
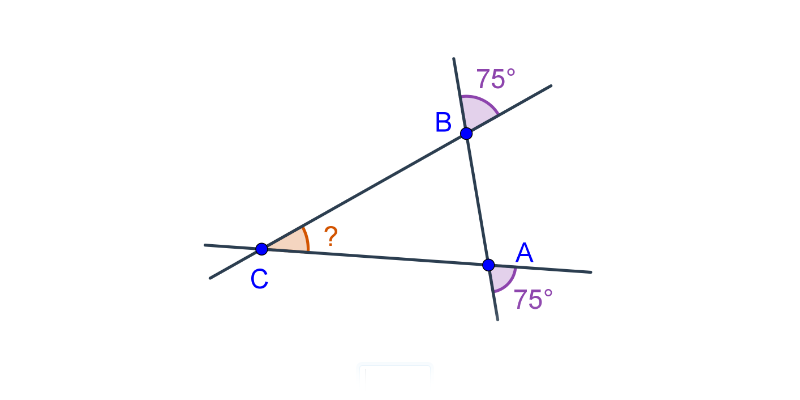
Kąty w trójkącie

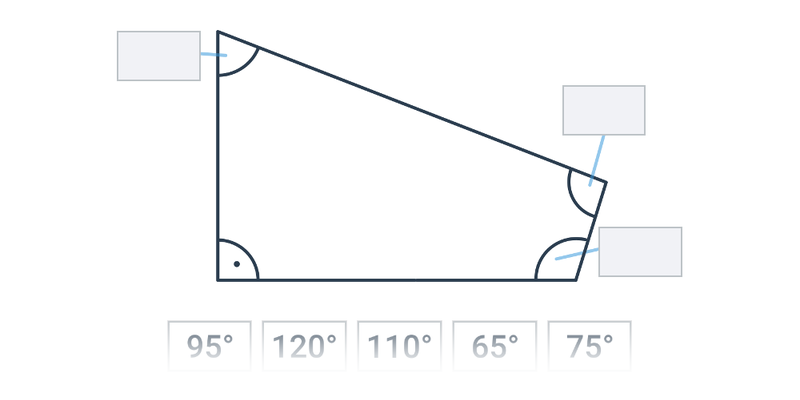
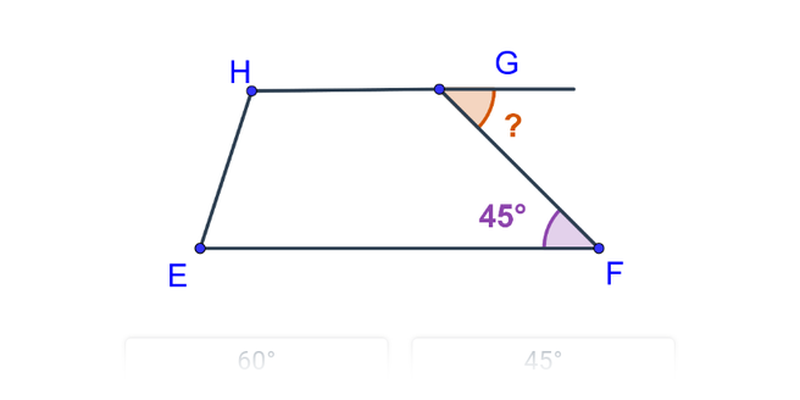
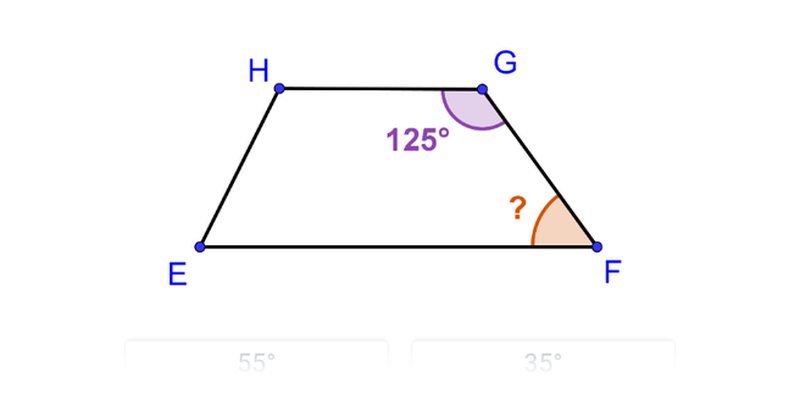
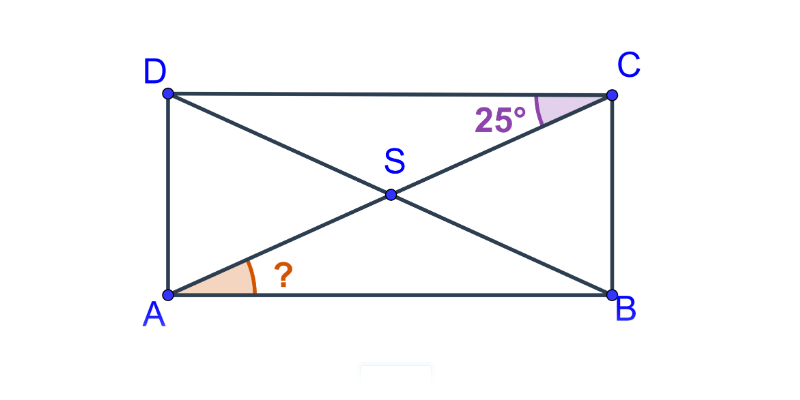
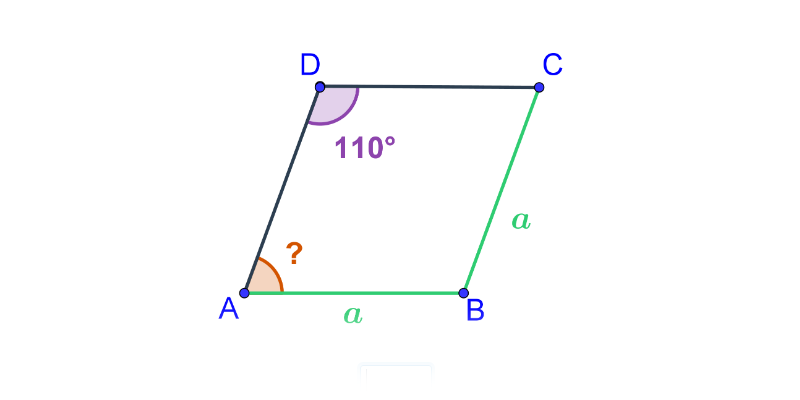
Kąty w czworokącie

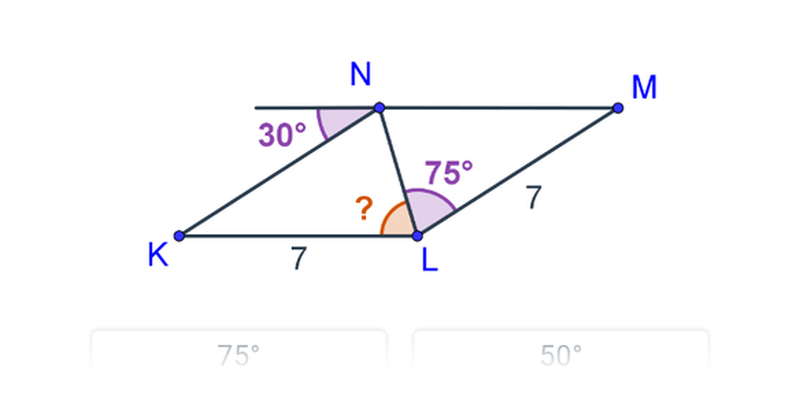
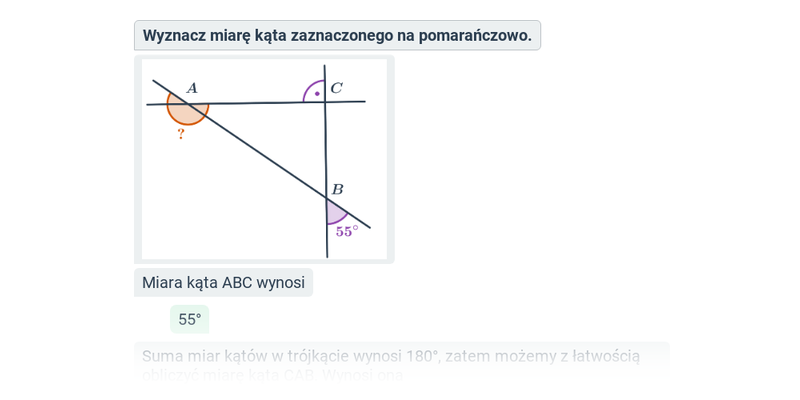
Kąty i wielokąty

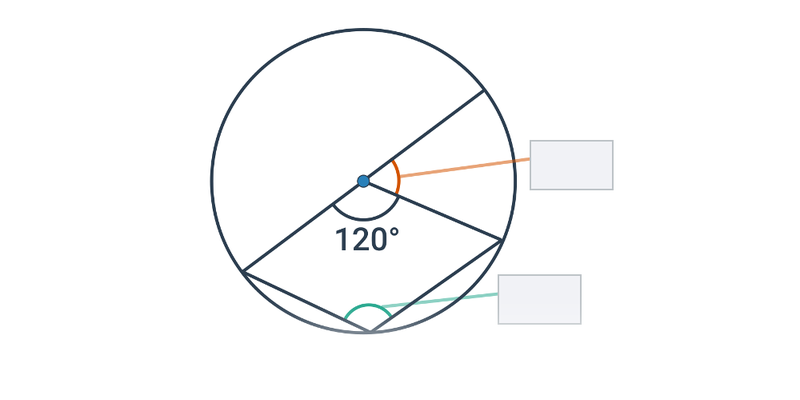
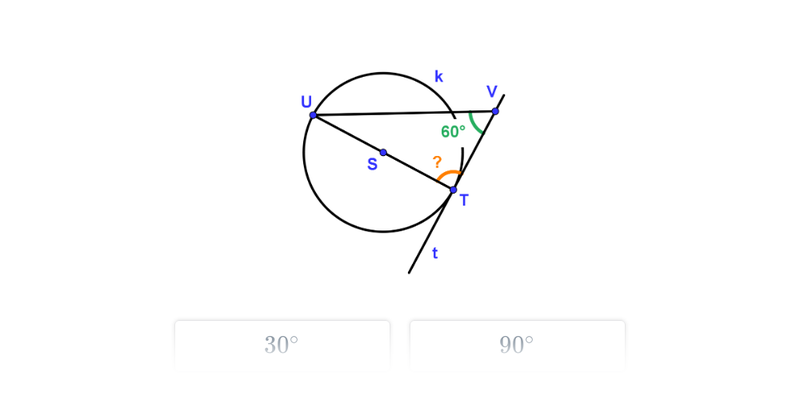
Kąty i okrąg

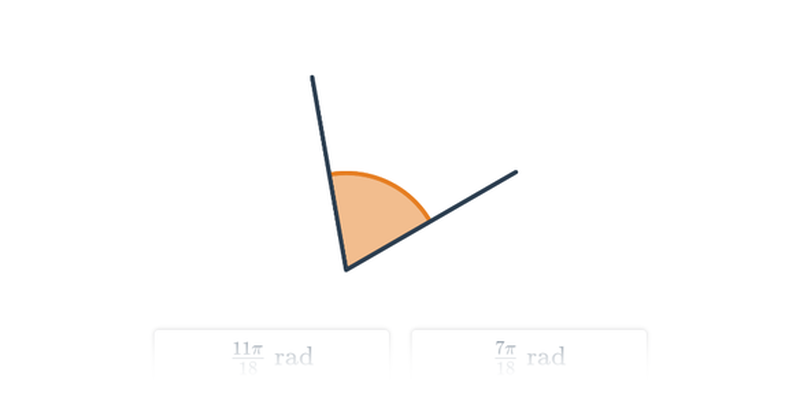
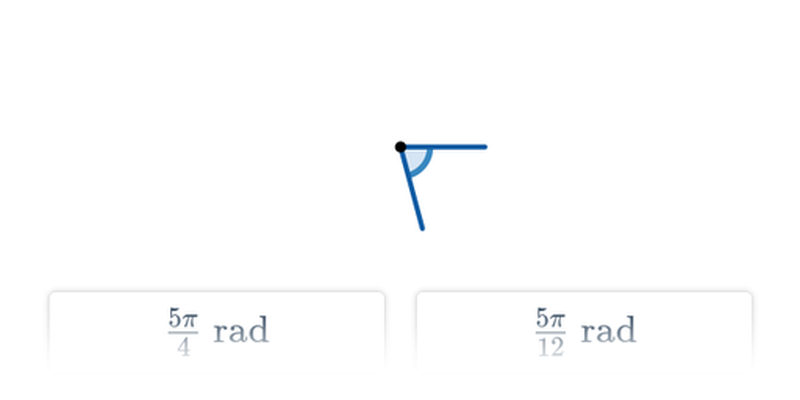
Radiany
Konstrukcje geometryczne
Konstrukcje geometryczne: oznaczenia

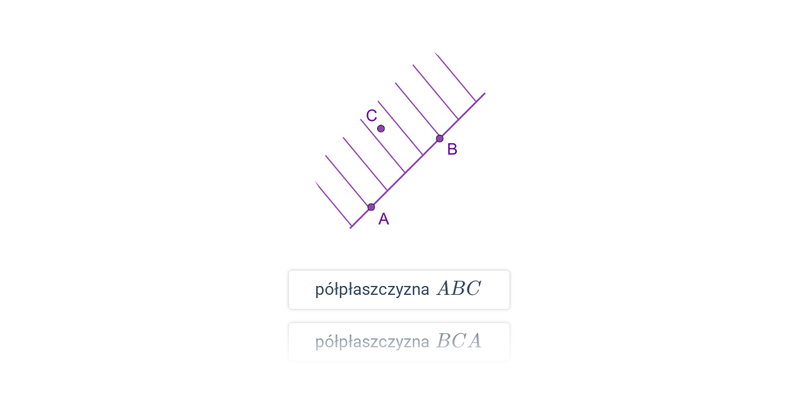
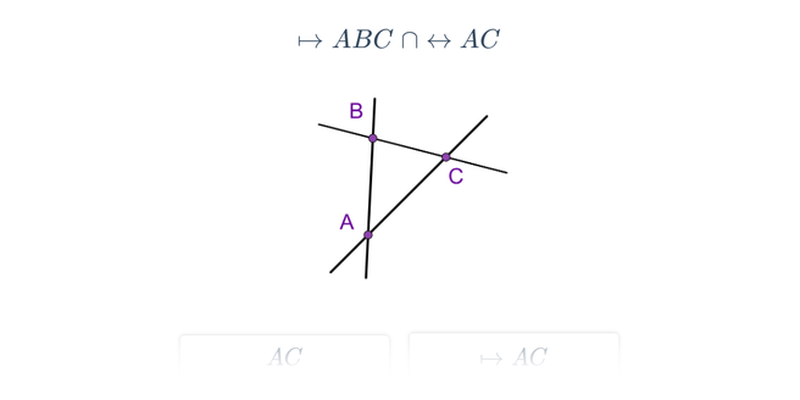
Półproste i półpłaszczyzny
Zadania konstrukcyjne: trójkąty
Konstrukcje trójkątów: znane długości boków
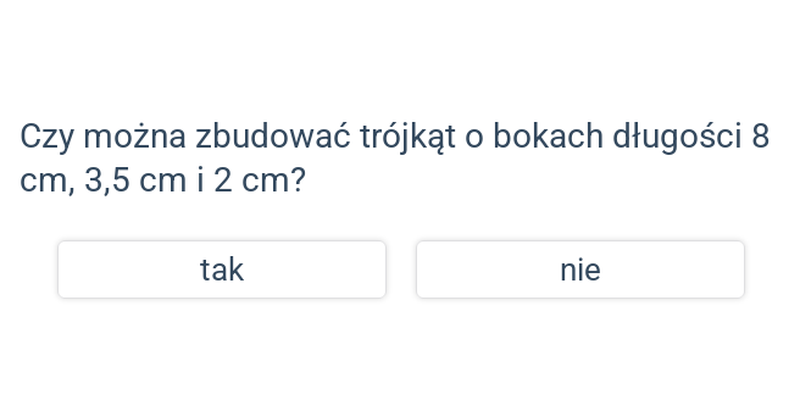
Nierówność trójkąta
Działania i własności na płaszczyźnie
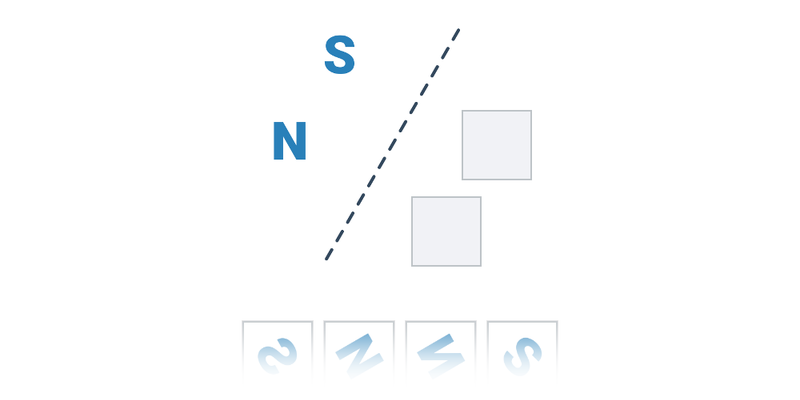
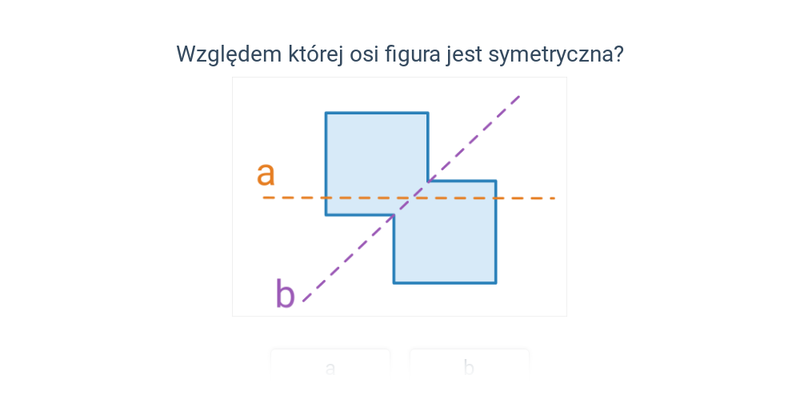
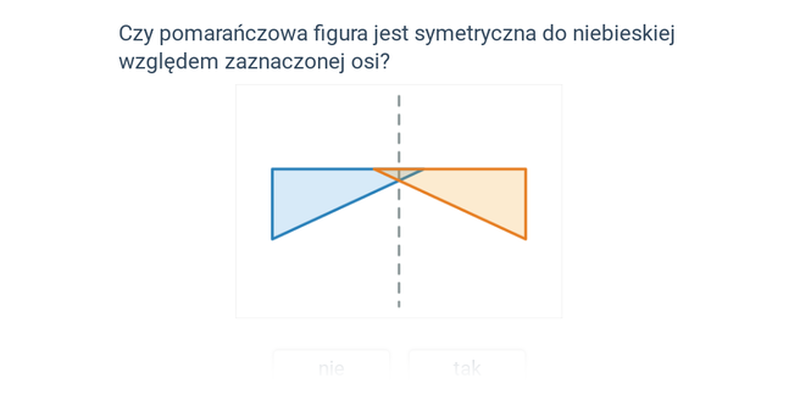
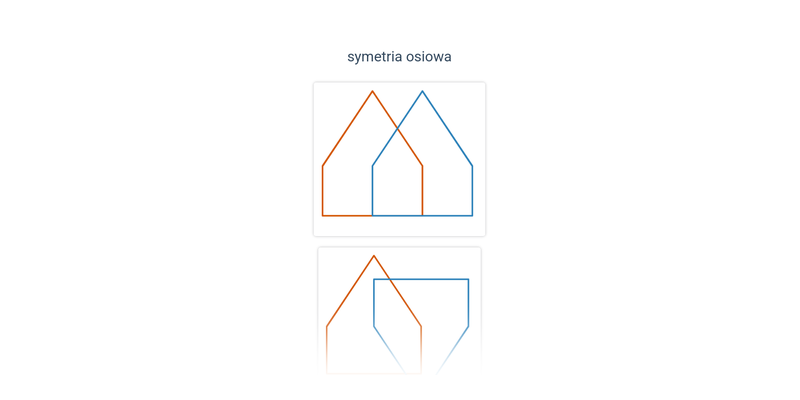
Symetria osiowa

Symetria środkowa

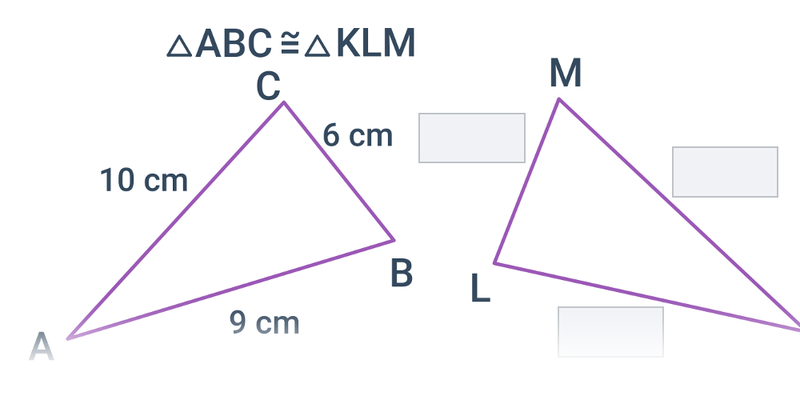
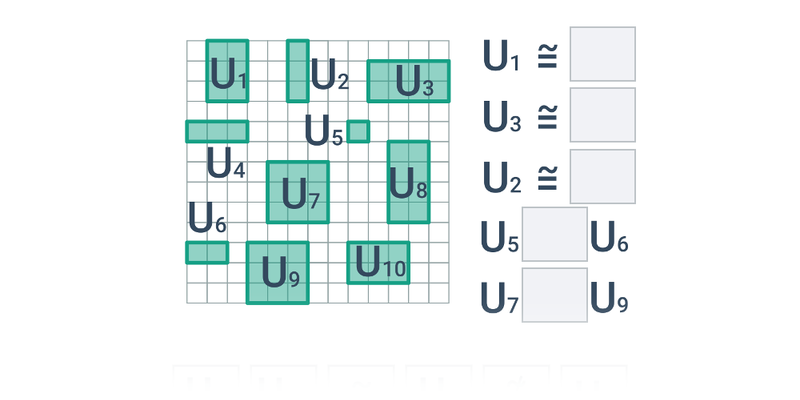
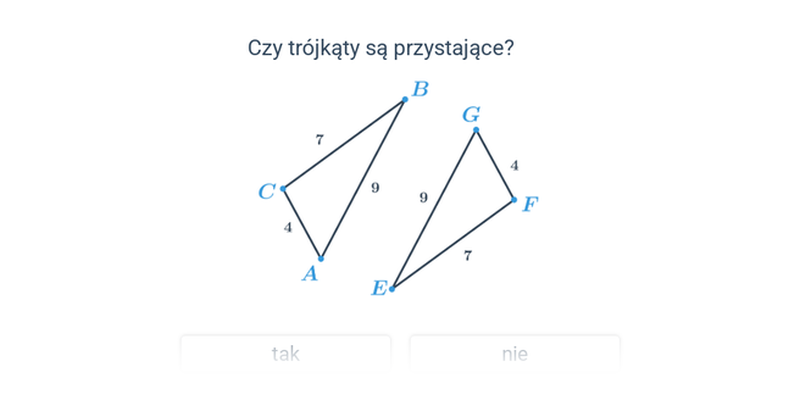
Przystawanie

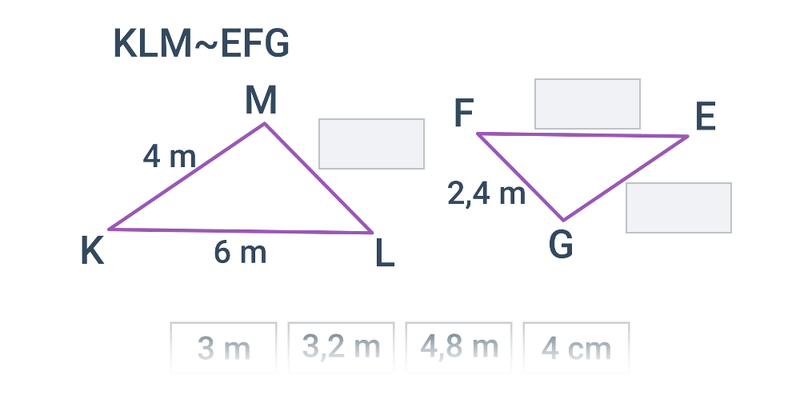
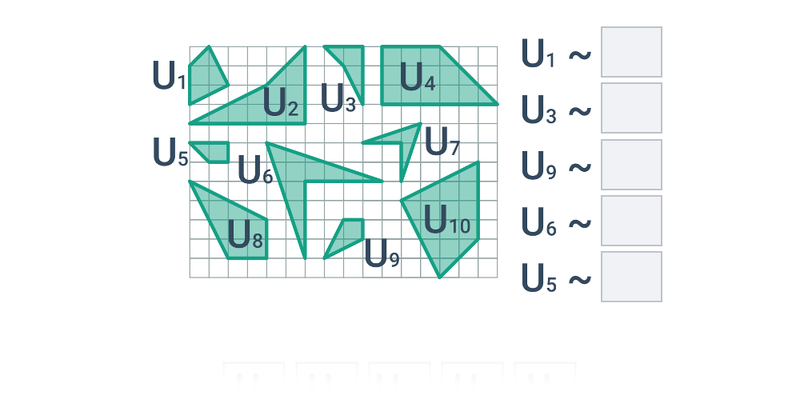
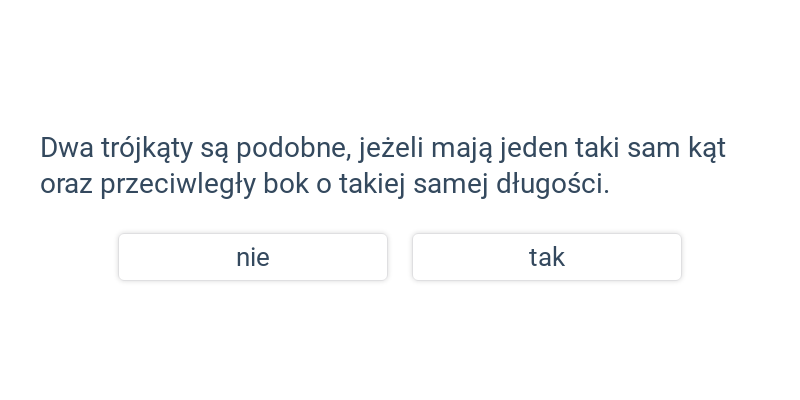
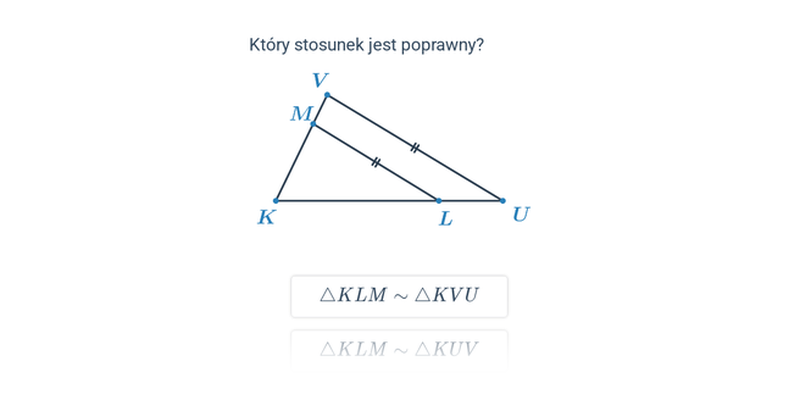
Podobieństwo

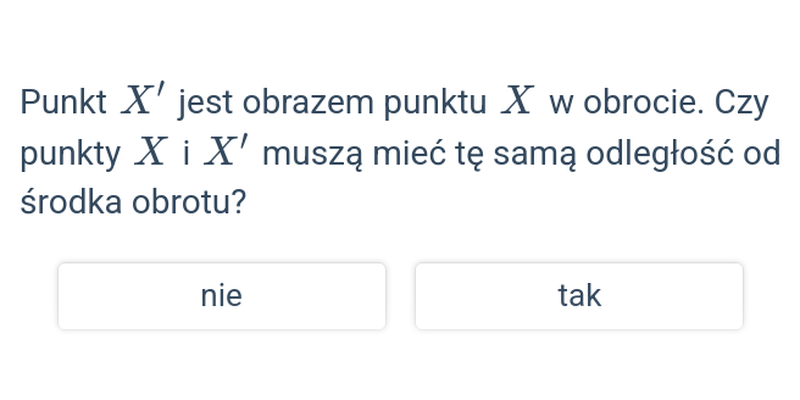
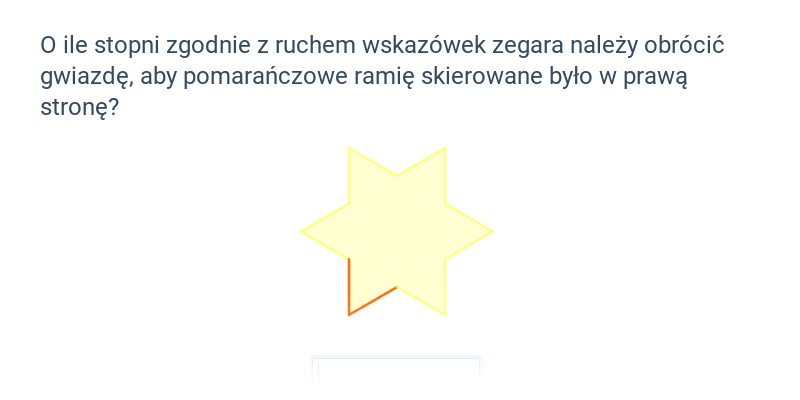
Obrót
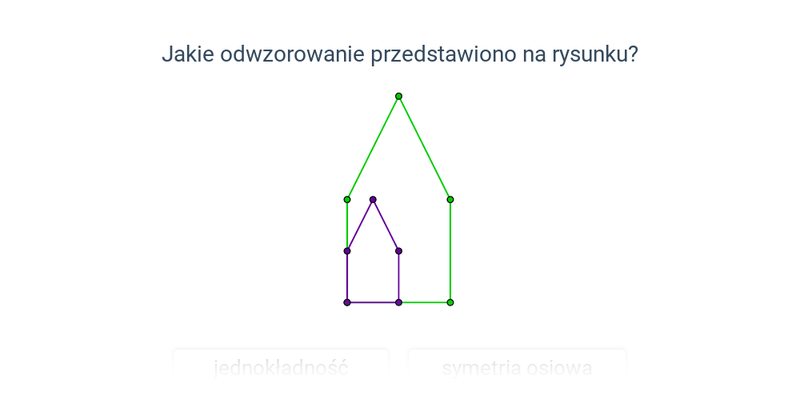
Odwzorowanie na płaszczyźnie
Rozpoznawanie symetrii osiowej i środkowej
Rodzaje przekształceń izometrycznych na płaszczyźnie
Działania i własności na płaszczyźnie: różne przykłady
Geometria analityczna
Punkty
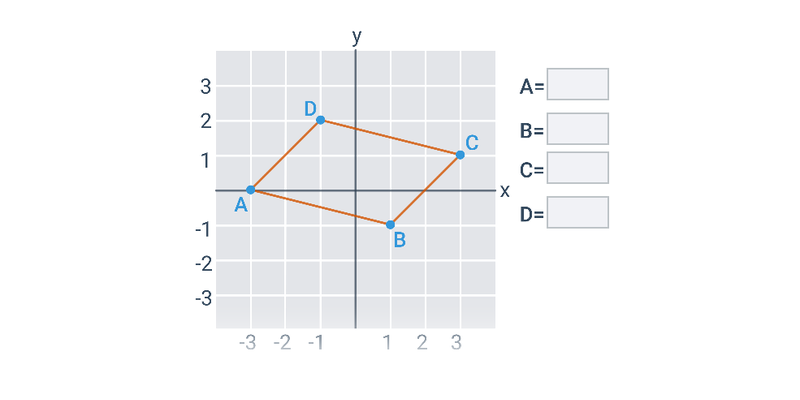
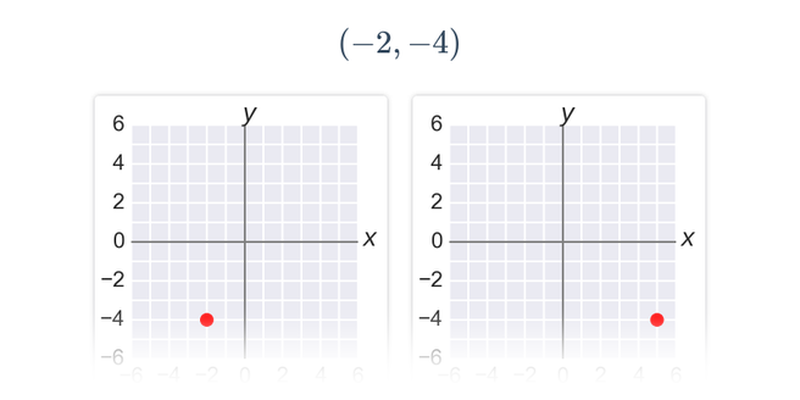
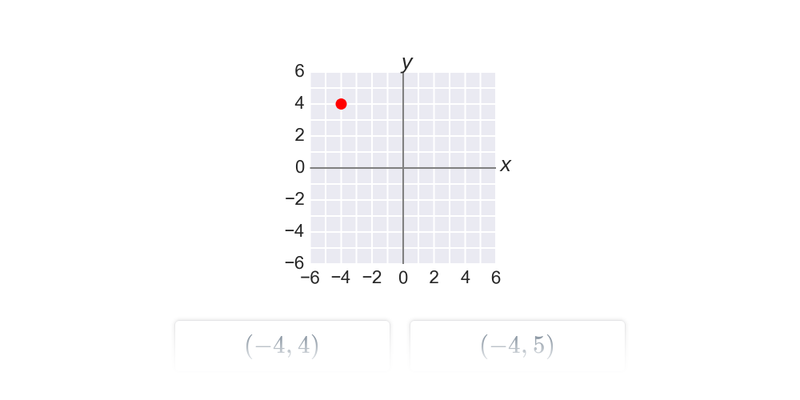
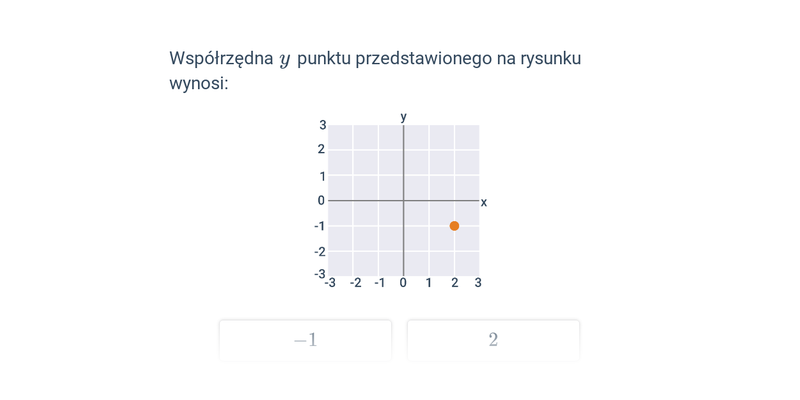
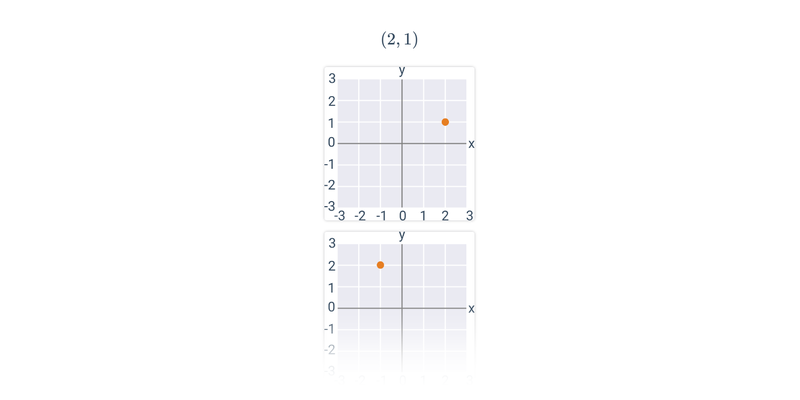
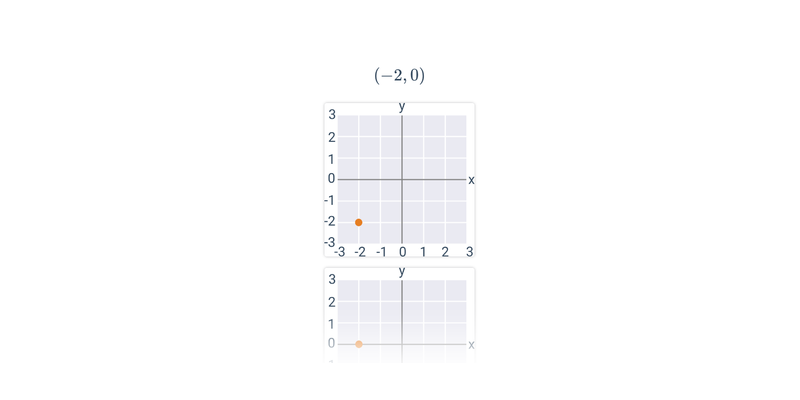
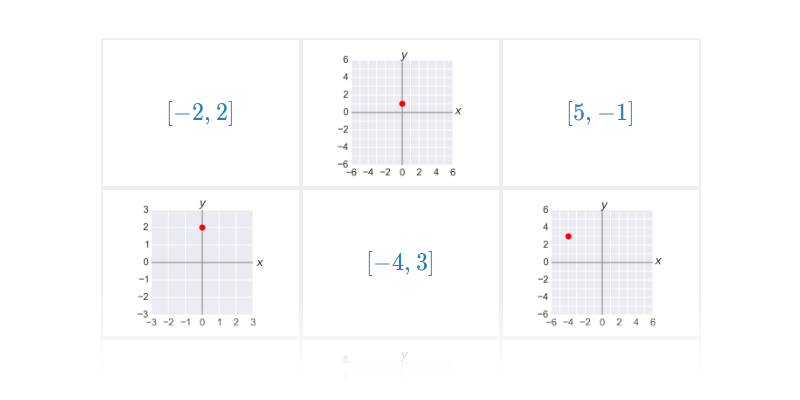
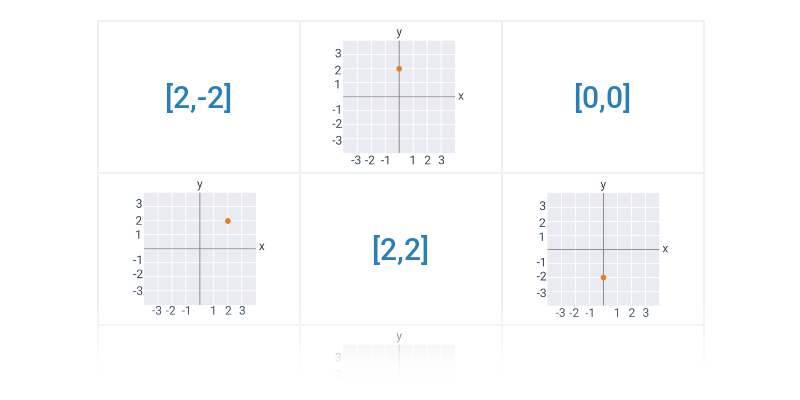
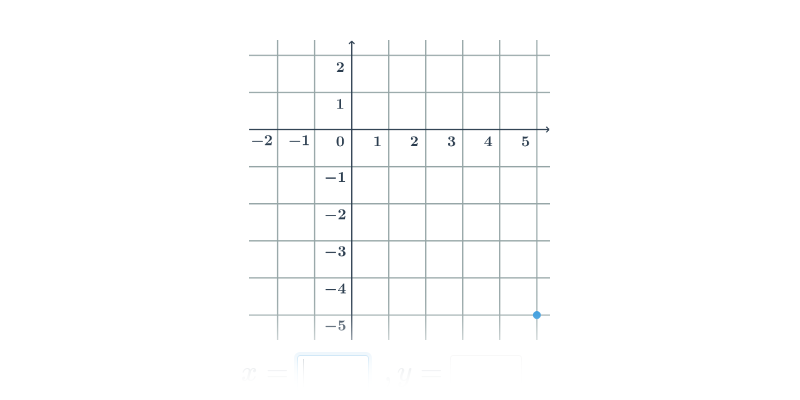
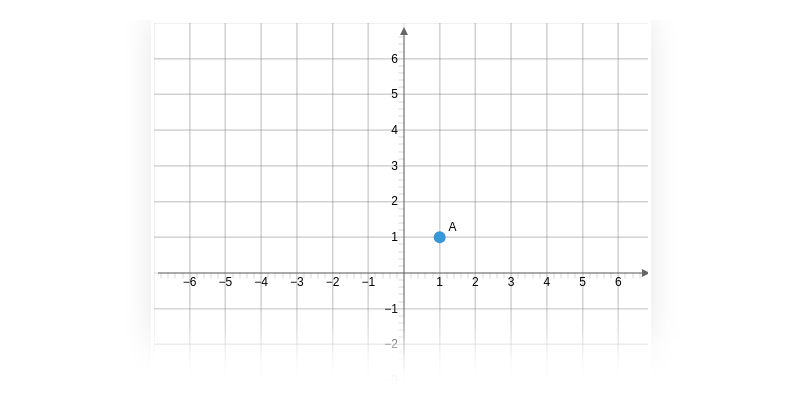
Współrzędne punktów w ukł. współrzędnych

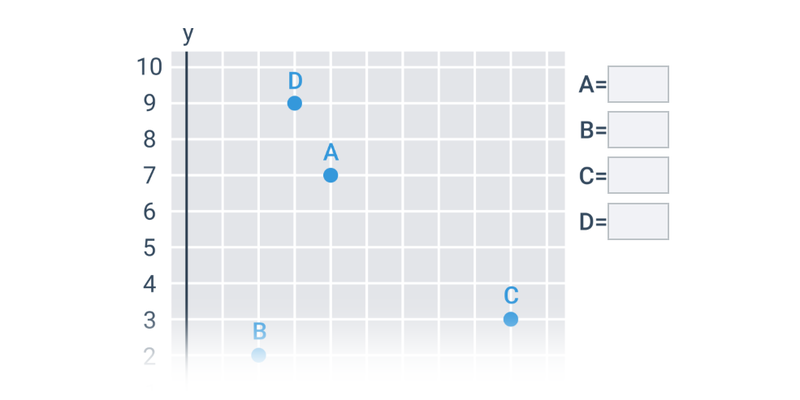
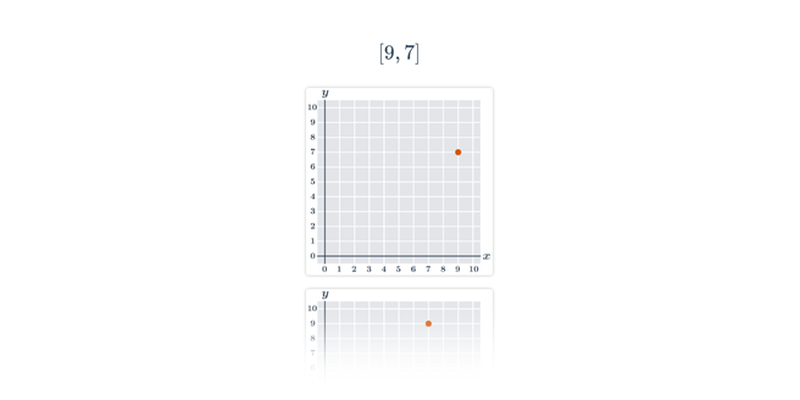
Współrzędne punktów w ukł. współrzędnych: pierwsza ćwiartka
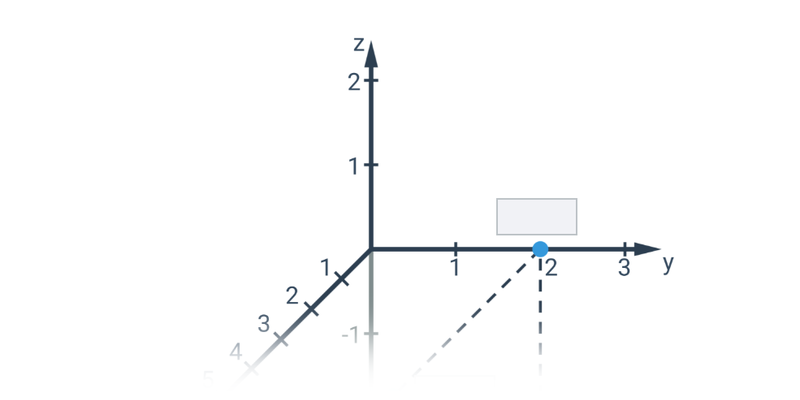
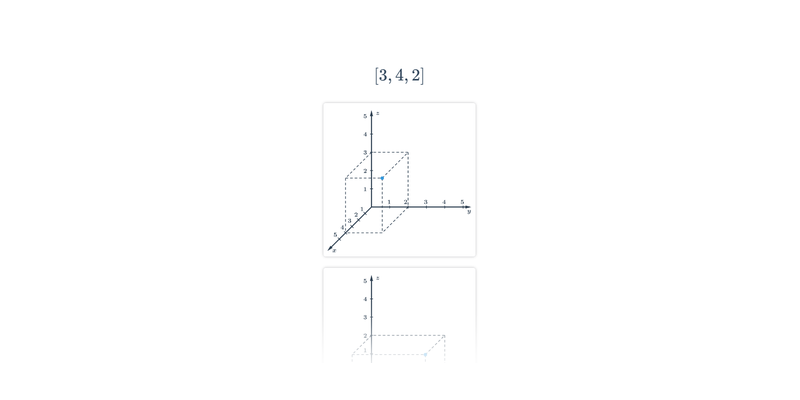
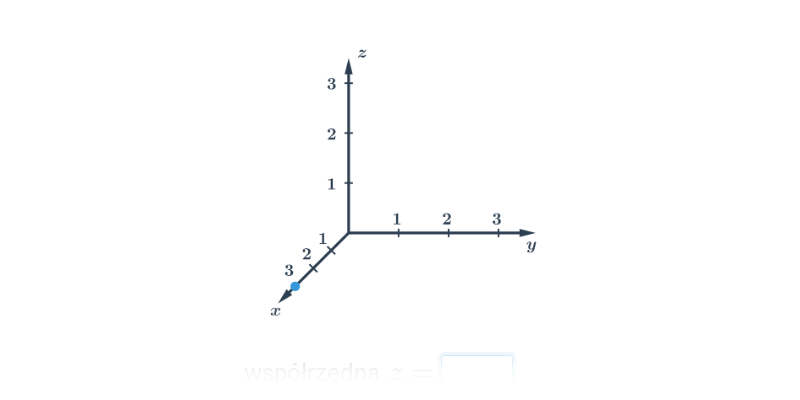
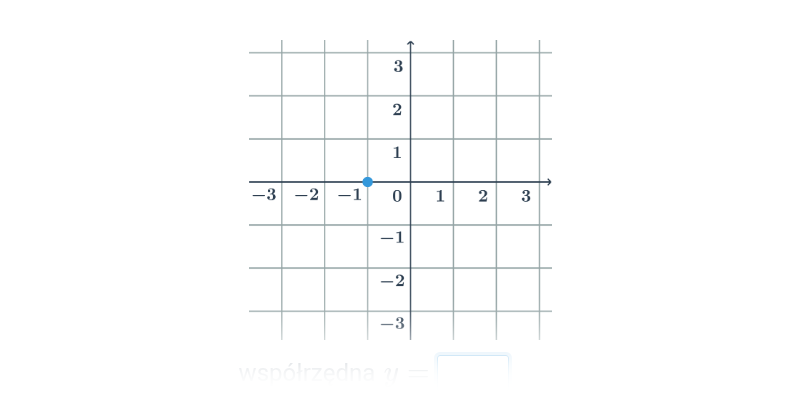
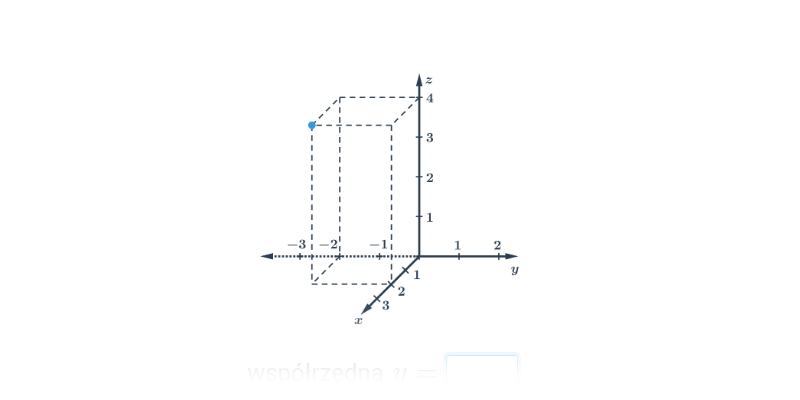
Współrzędne punktów w przestrzeni
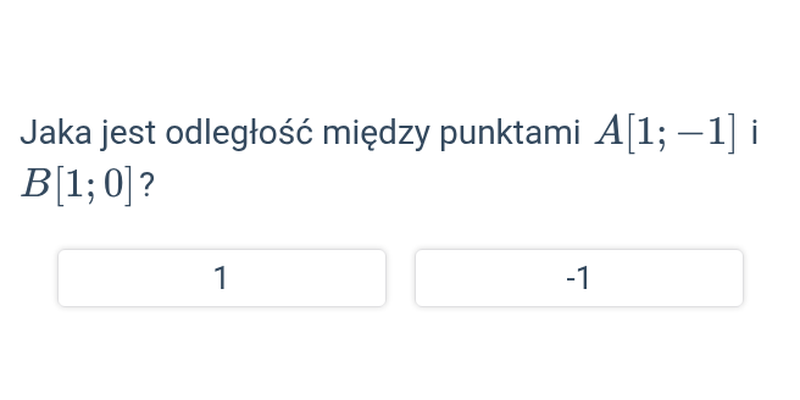
Odległość między punktami w ukł. współrzędnych

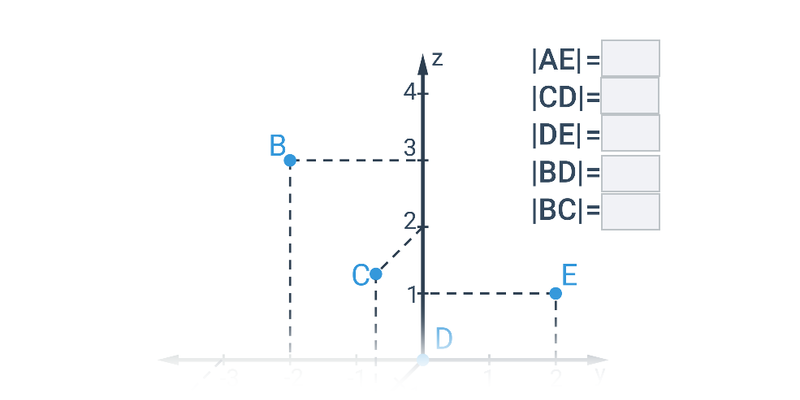
Odległość między punktami w przestrzeni

Punkty: miks przykładów
Odcinki
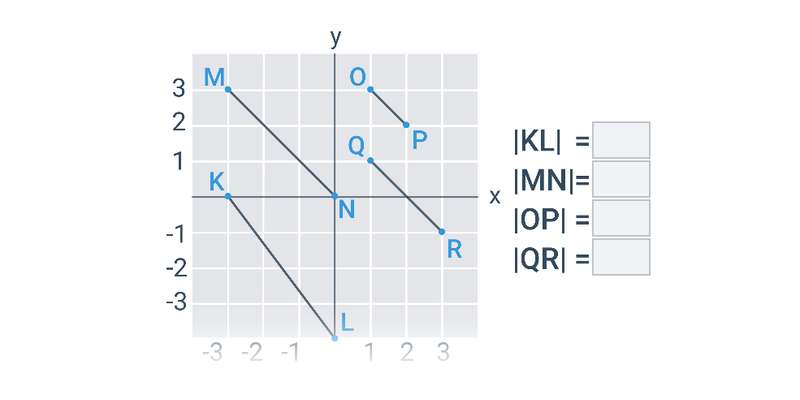
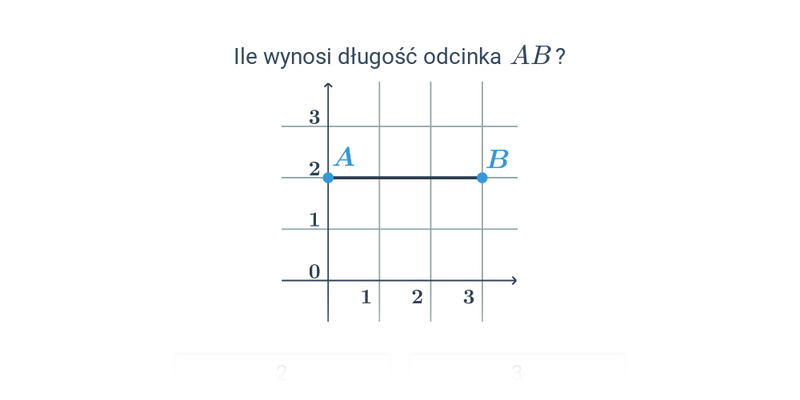
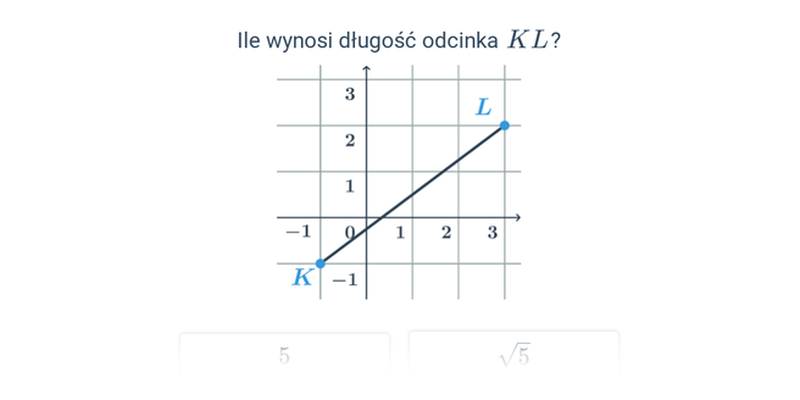
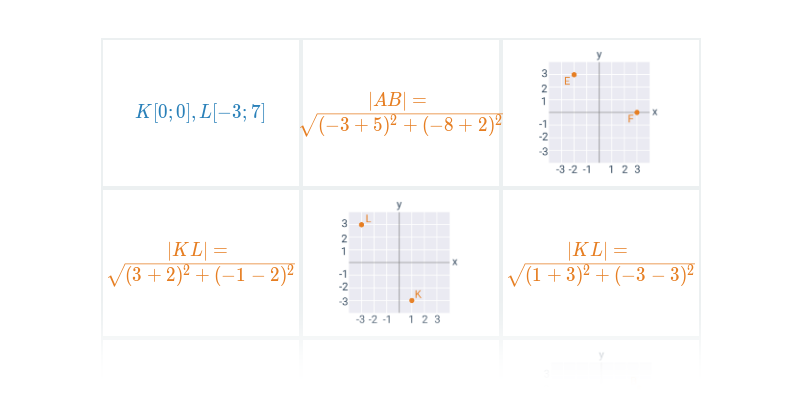
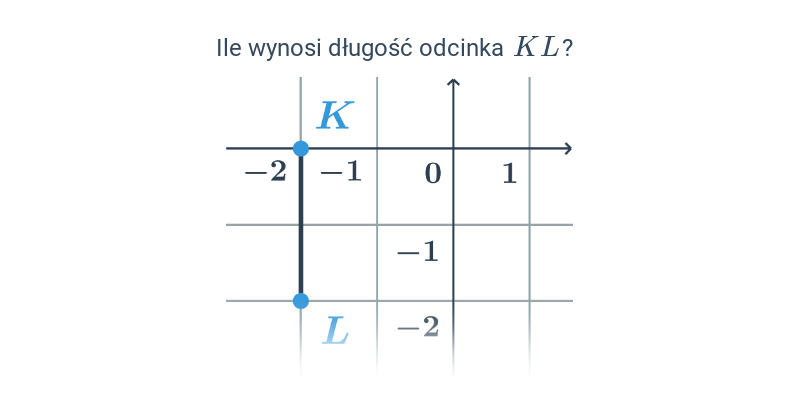
Długość odcinka w ukł. współrzędnych

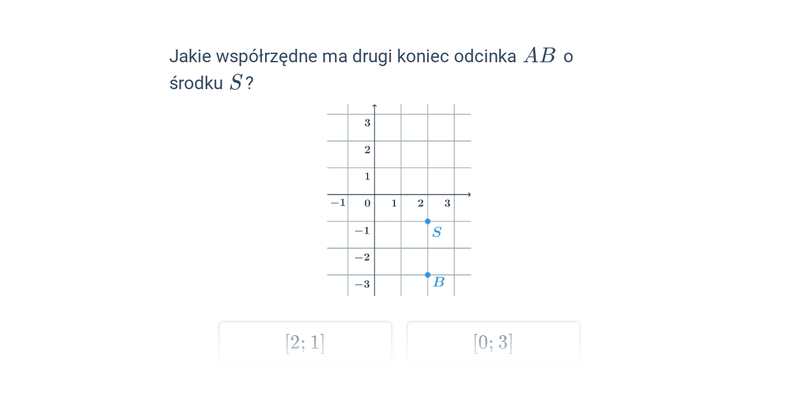
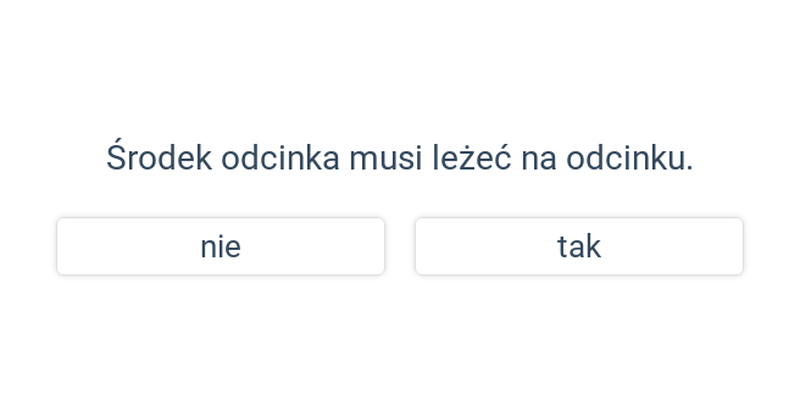
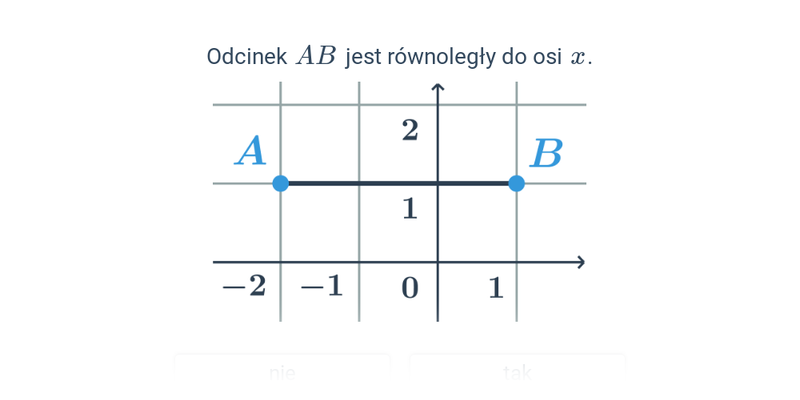
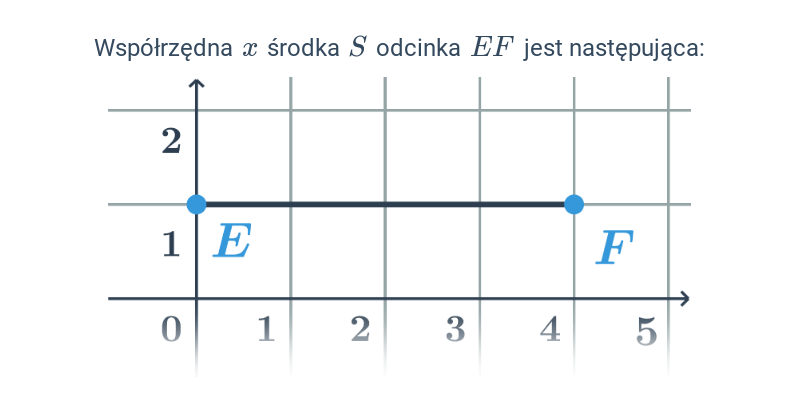
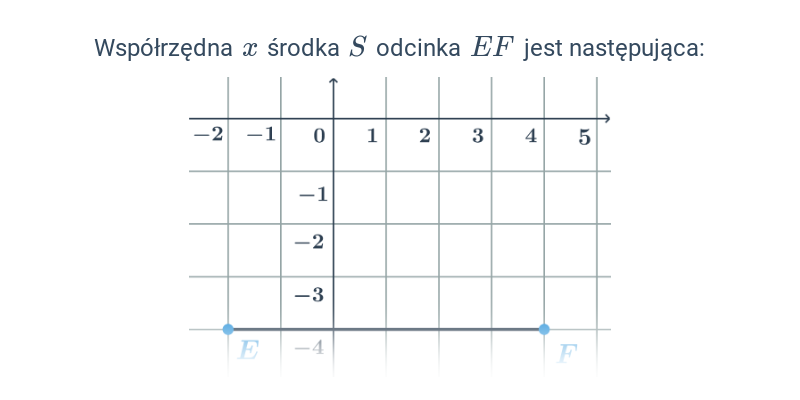
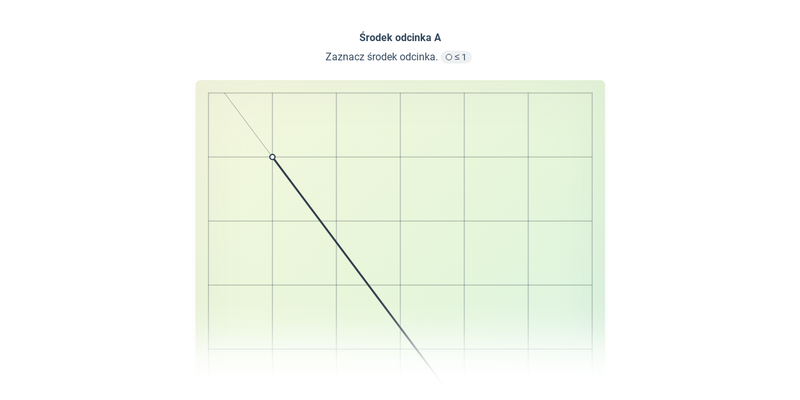
Środek odcinka w ukł. współrzędnych

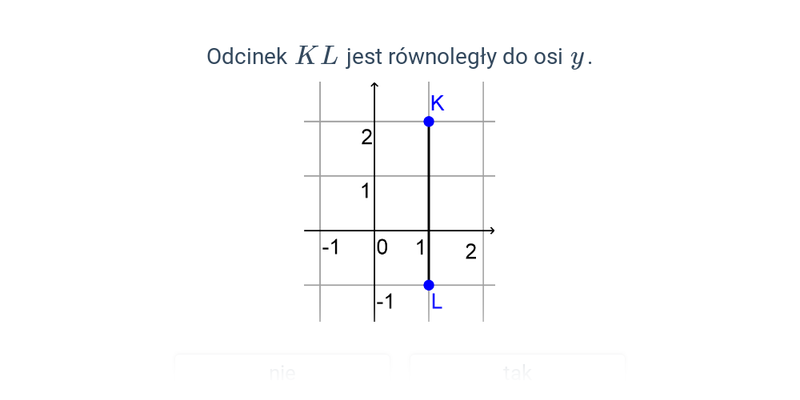
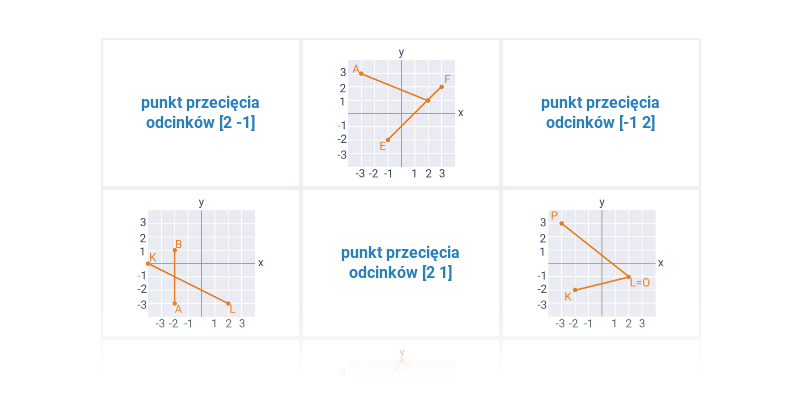
Wzajemne położenie odcinków w ukł. współrzędnych
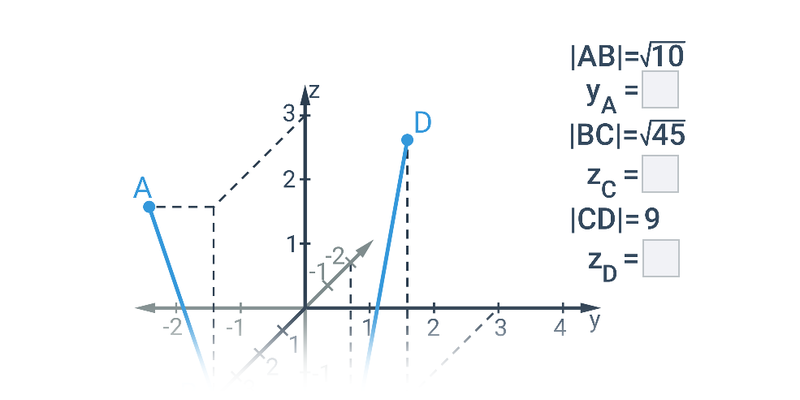
Długość odcinka w przestrzeni

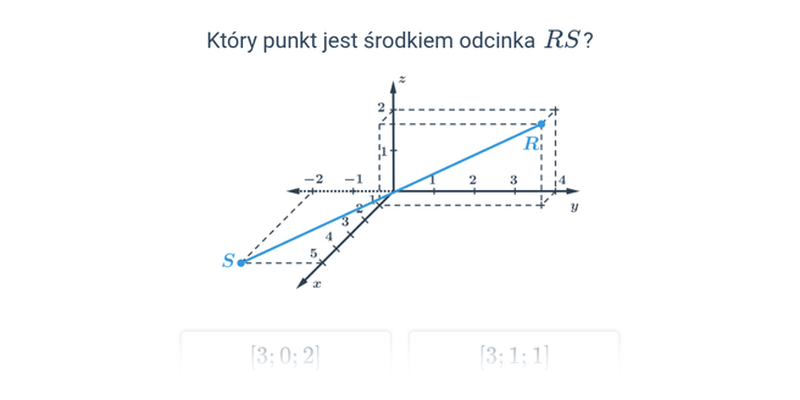
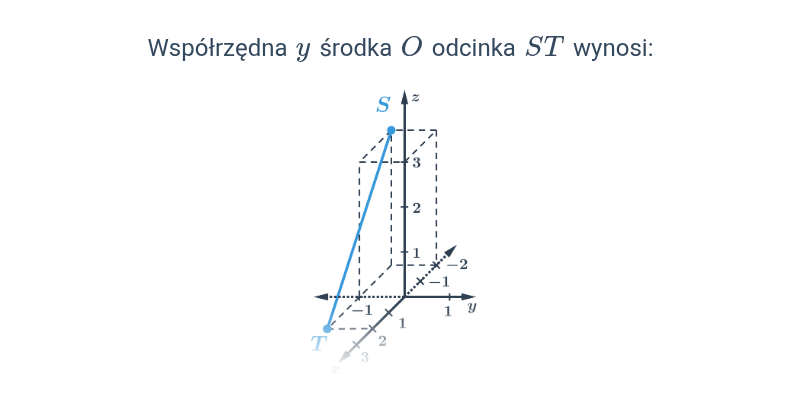
Środek odcinka w przestrzeni
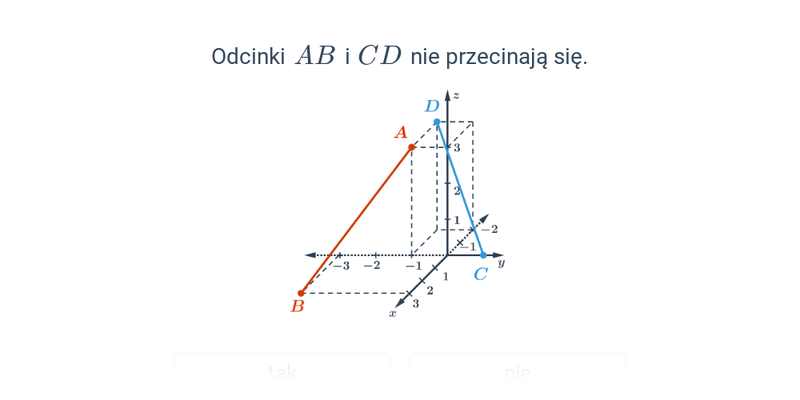
Wzajemne położenie odcinków w przestrzeni
Odcinki: miks przykładów
Wektory
Wektory: pojęcia

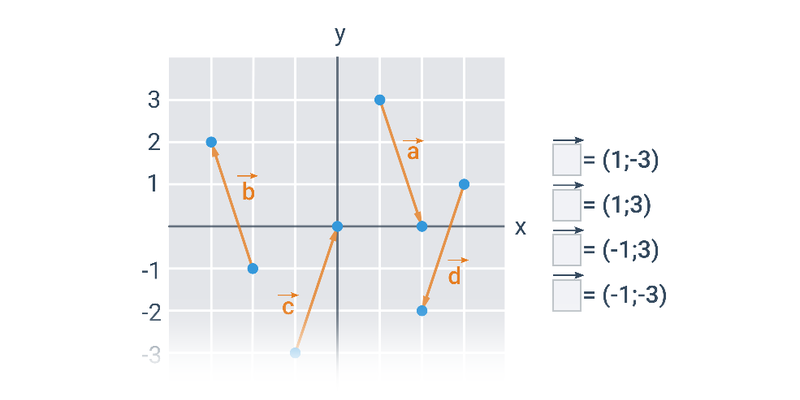
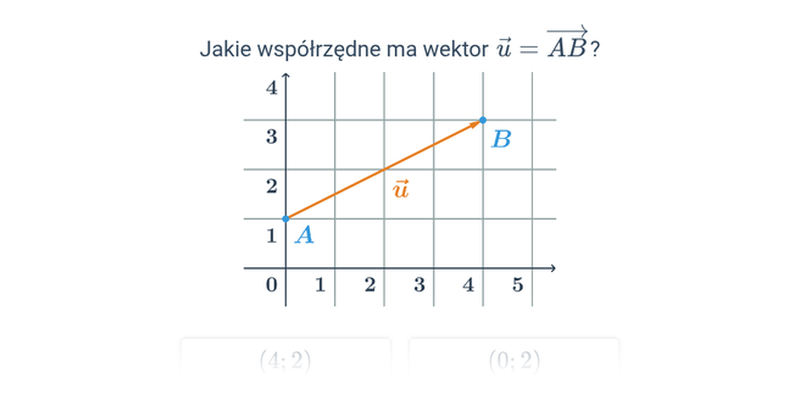
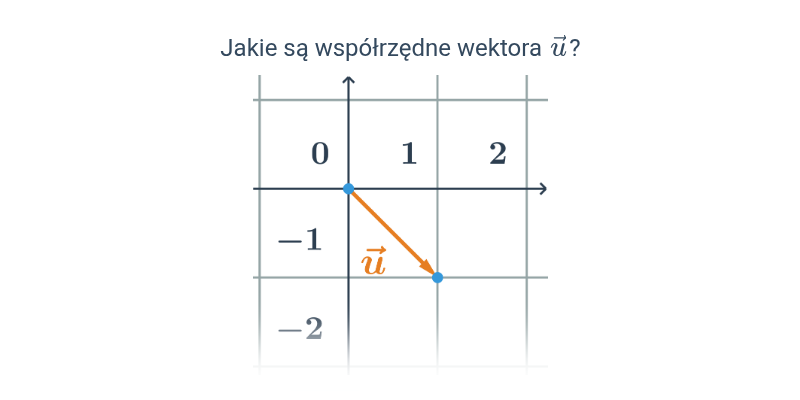
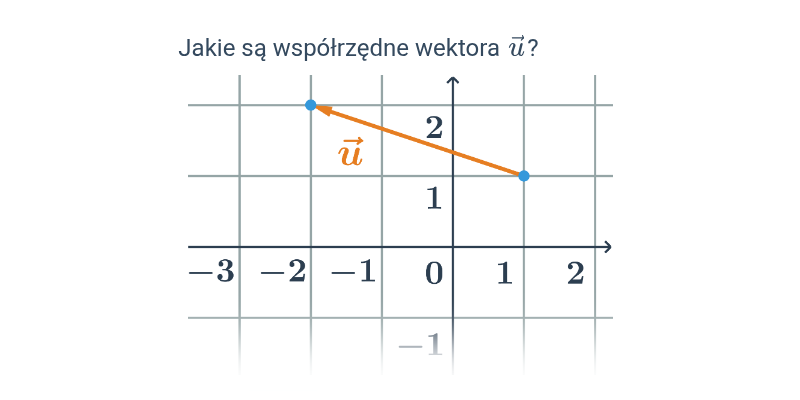
Współrzędne wektora

Wektory: współrzędne w przestrzeni
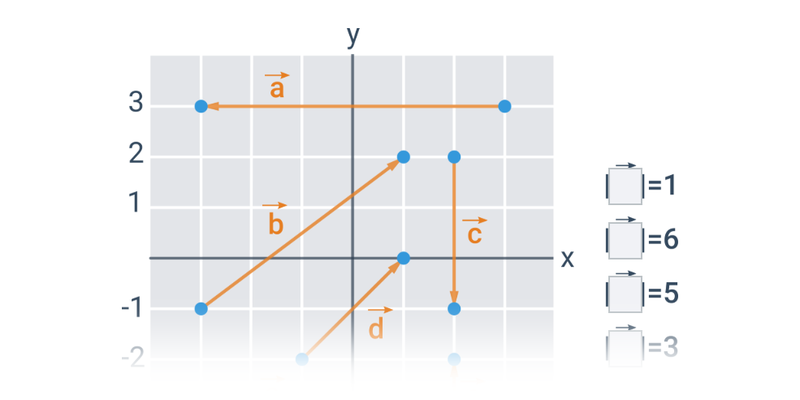
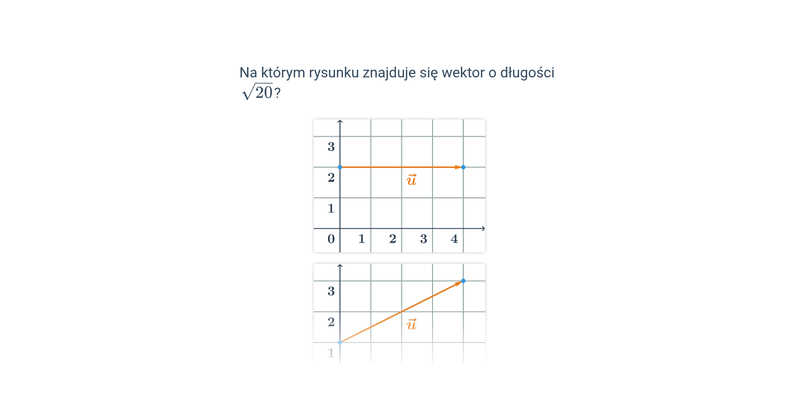
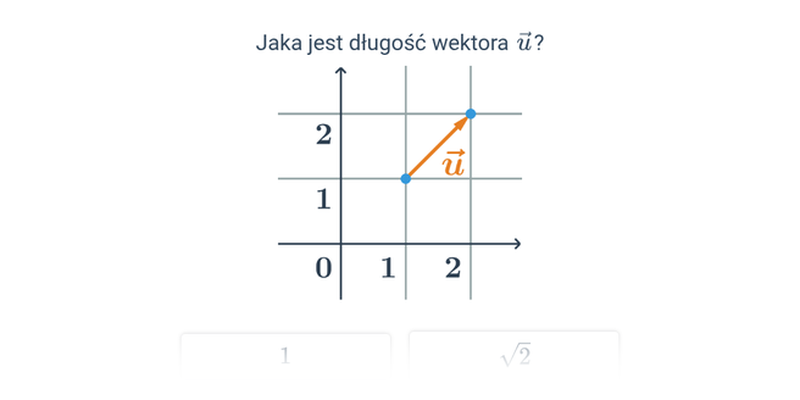
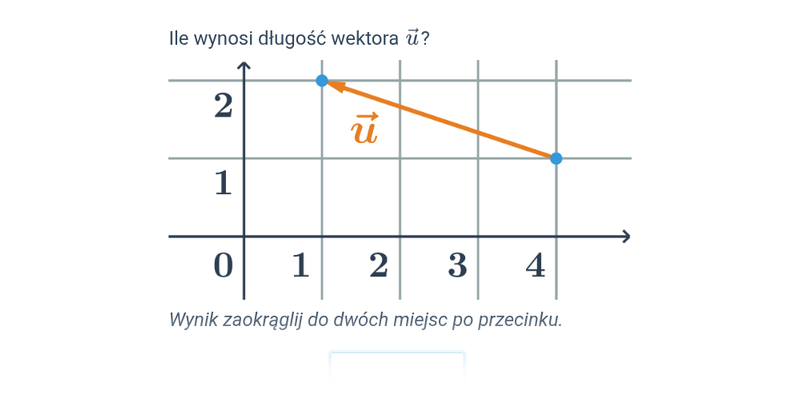
Długość wektora

Wzajemne położenie wektorów
Wektory: miks przykładów
Działania na wektorach
Wektory: mnożenie przez stałą, suma, różnica
Wektory: iloczyn skalarny

Działania na wektorach: miks przykładów
Proste
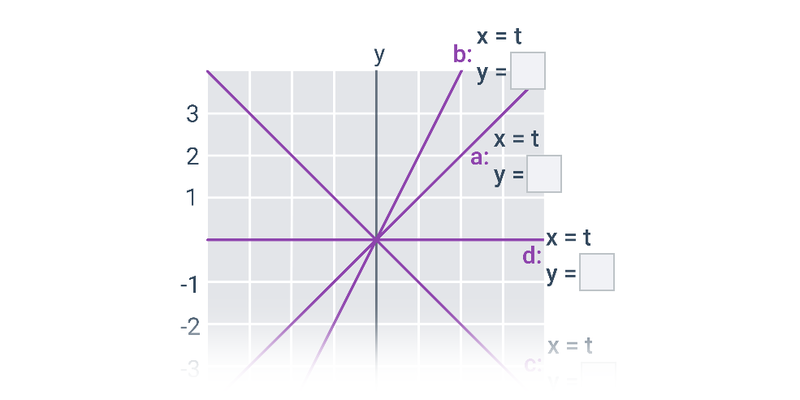
Proste: pojęcia
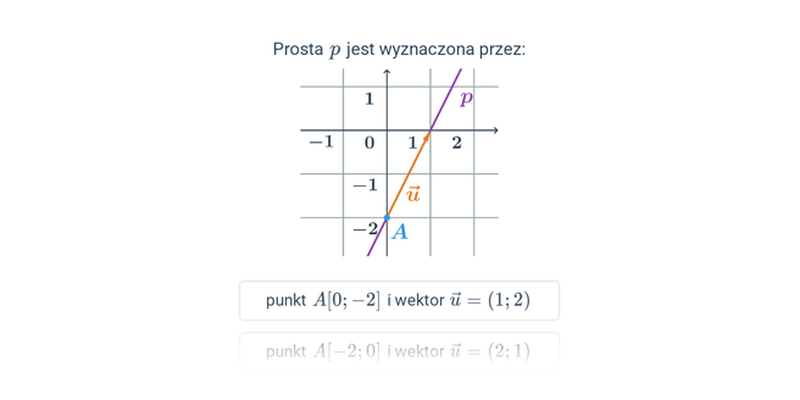
Wyznaczanie prostej

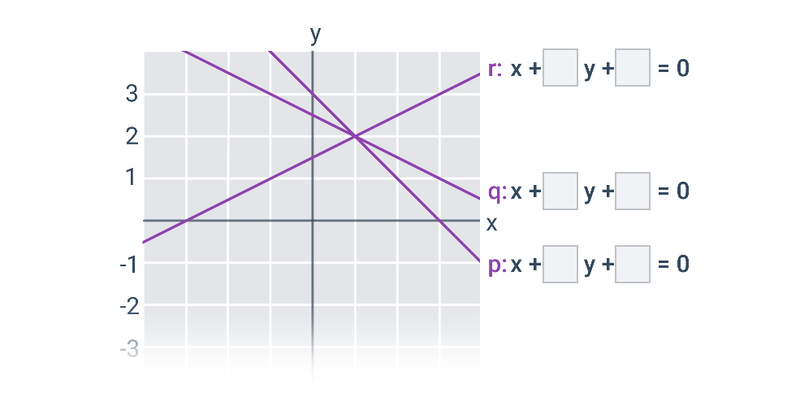
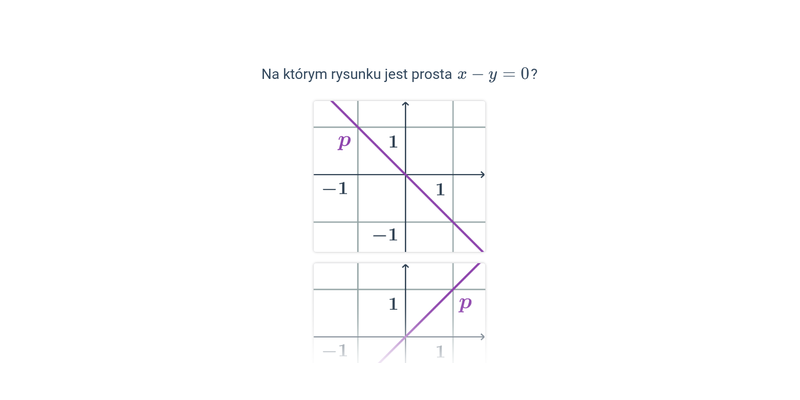
Równanie ogólne prostej w ukł. współrzędnych

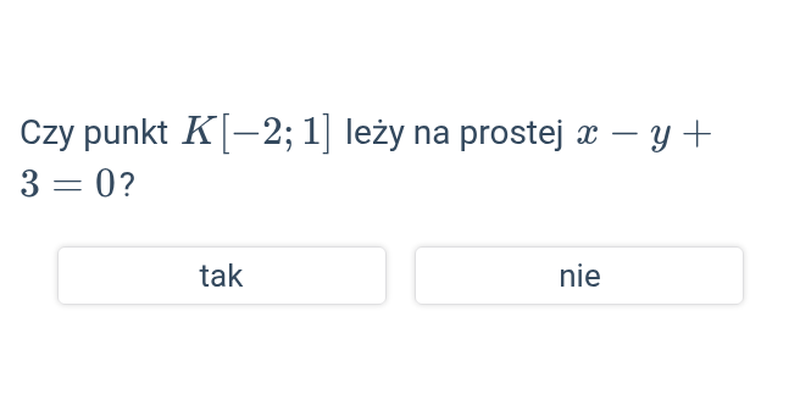
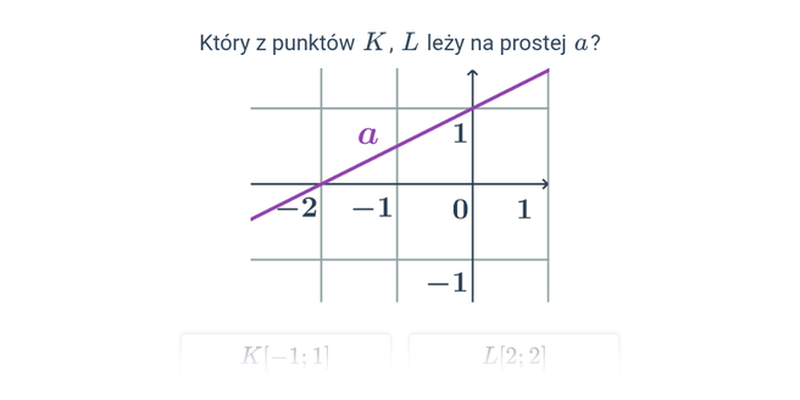
Wzajemne położenie prostej i punktu w ukł. współrzędnych
Proste: miks przykładów
Płaszczyzny
Wzajemne położenie punktu i płaszczyzny
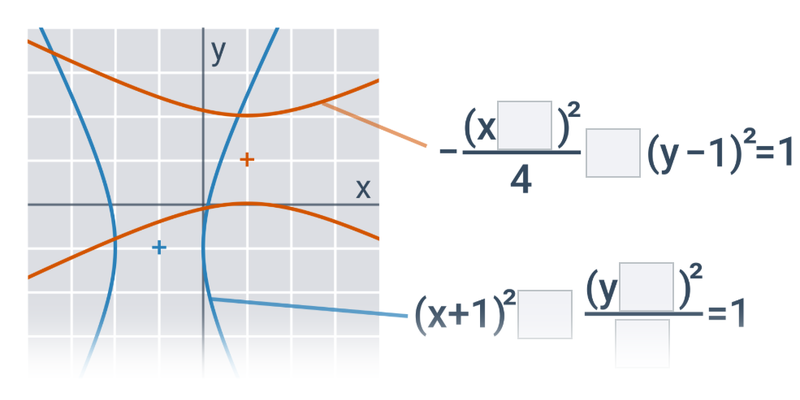
Krzywe stożkowe
Krzywe stożkowe: pojęcia
Okrąg: pojęcia
Parabola: pojęcia
Okrąg (krzywe stożkowe)
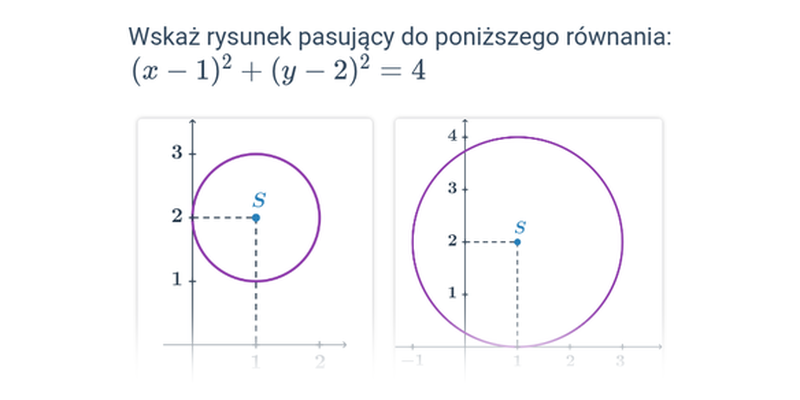
Okrąg: równanie ogólne
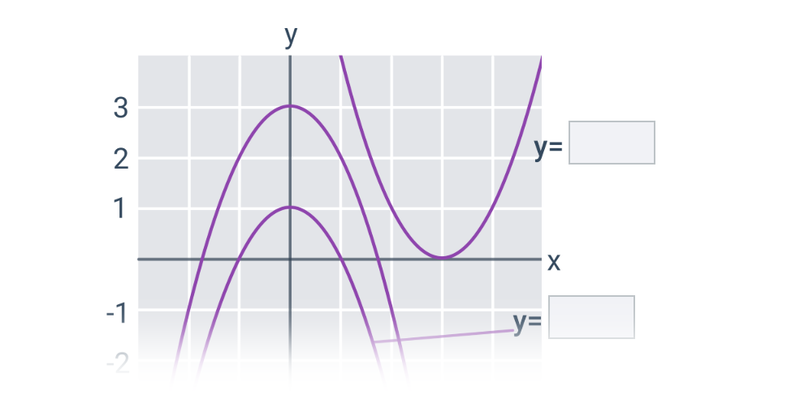
Parabola
Parabola: równanie