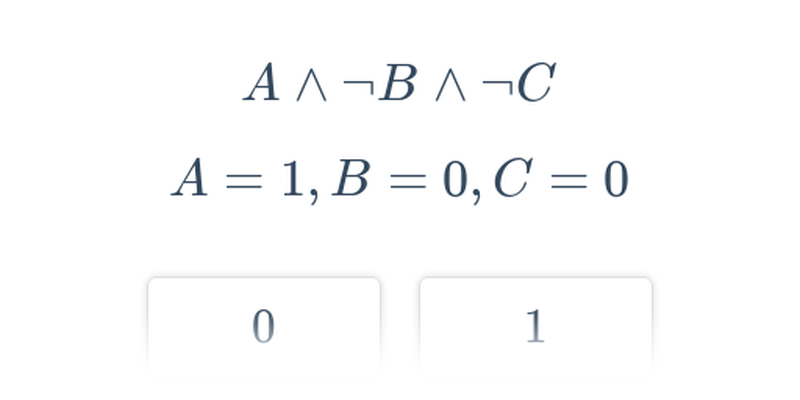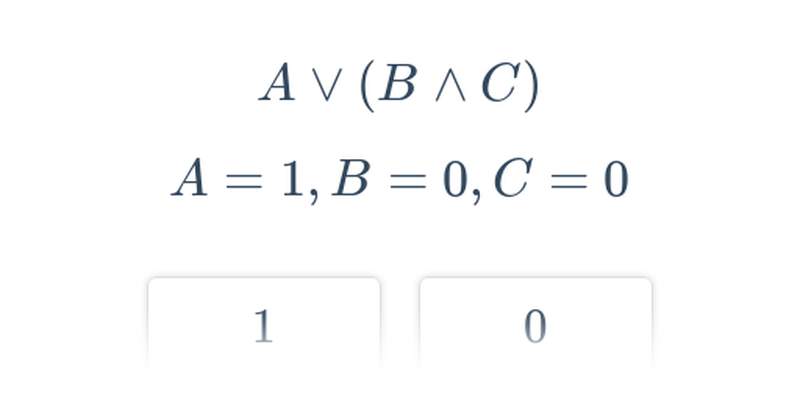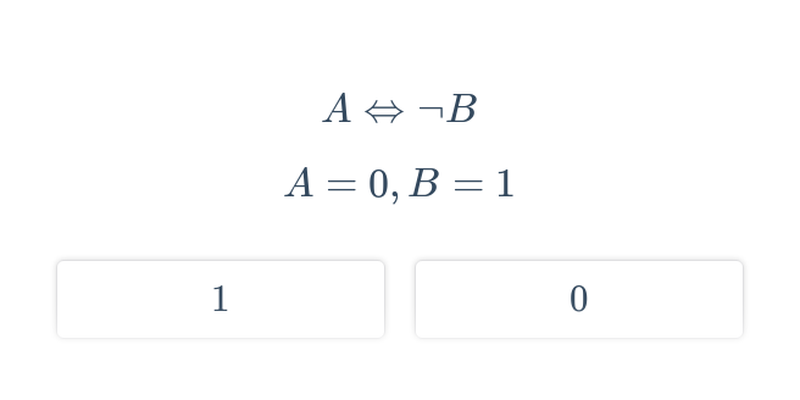Przesuwanie
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.
Kombinatoryka, zbiory, logika
Zbiory
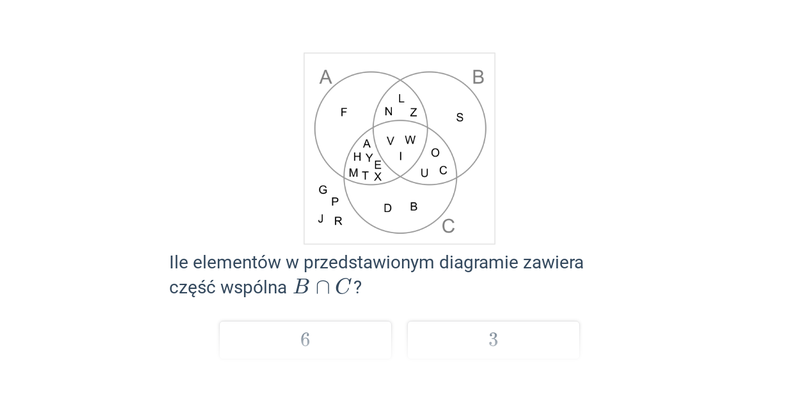
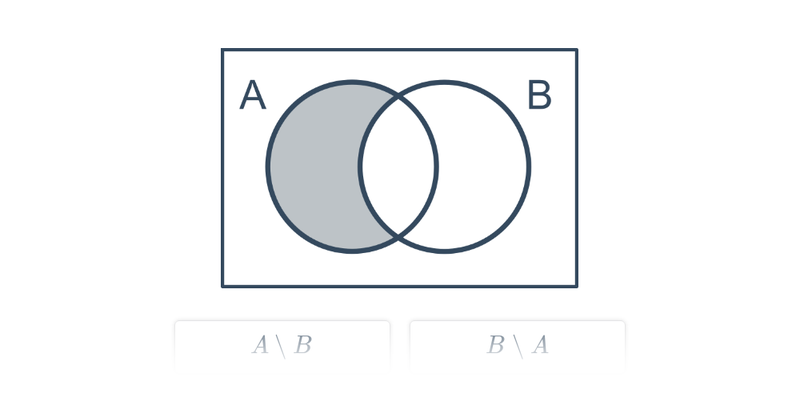
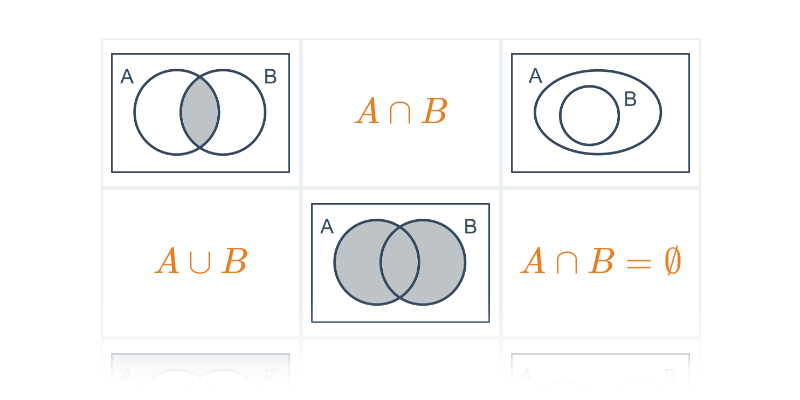
Diagramy Venna
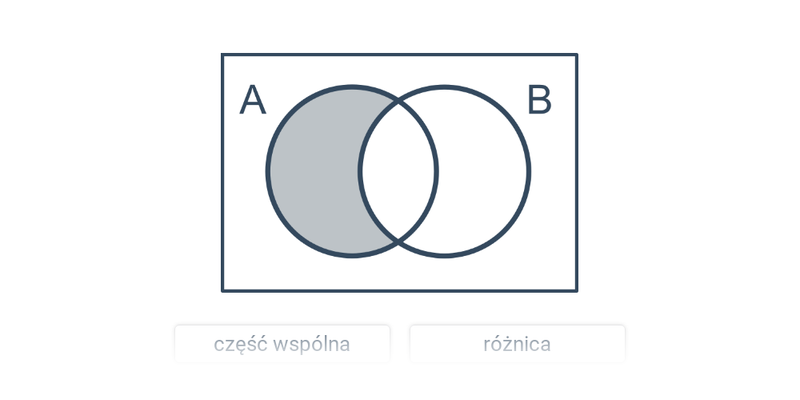
Decydowanie
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.
Kombinatoryka, zbiory, logika
Zbiory
Działania na zbiorach
Własności zbiorów i działań na zbiorach
Diagramy Venna
Potęgi potęg, zbiór potęgowy
Zbiory: miks przykładów
Logika
Logika: pojęcia i oznaczenia
Zdania logiczne
Morska logika
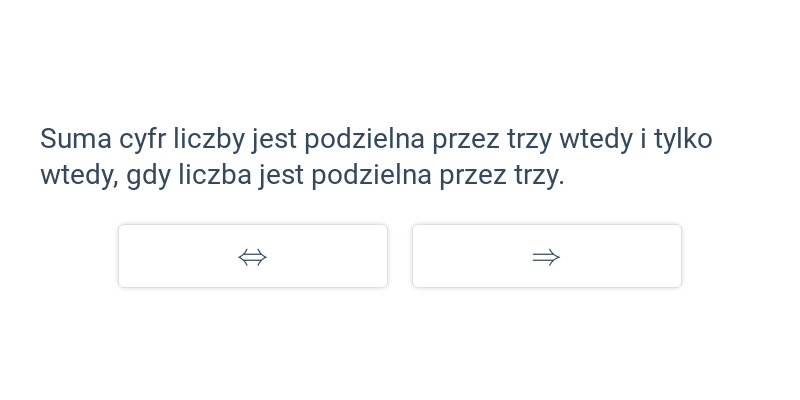
Ocena wyrażeń logicznych
Przekształcanie wyrażeń logicznych
Kwantyfikatory
Logika: miks przykładów
Kombinatoryka
Kombinatoryka: pojęcia
Rachunek prawdopodobieństwa
Podstawowe prawdopodobieństwo zdarzenia
Doświadczenia losowe i zdarzenia złożone
Statystyka opisowa
Średnia i mediana
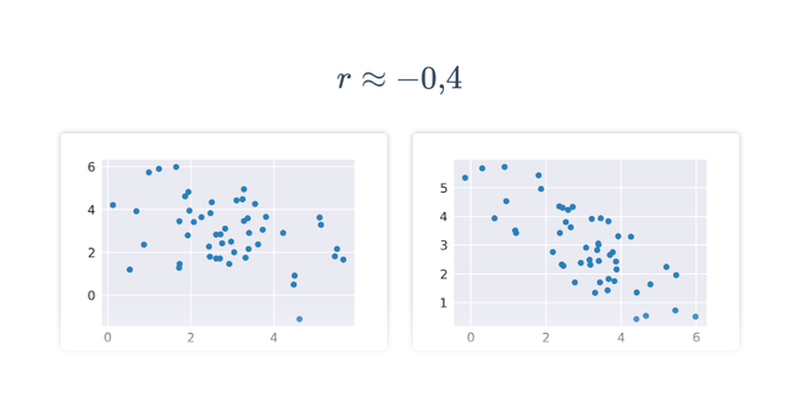
Współczynnik korelacji
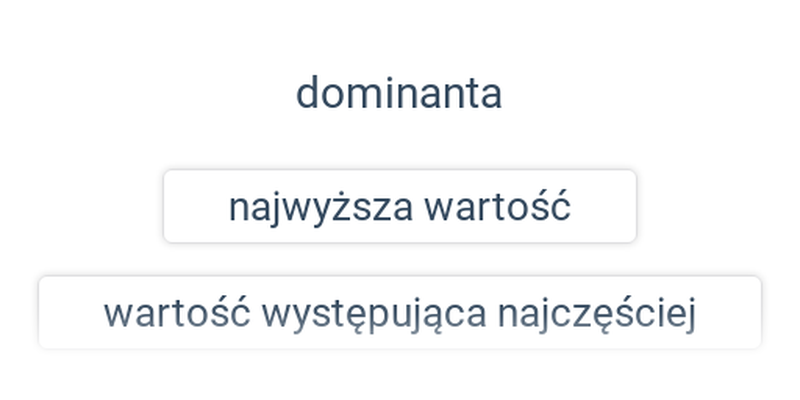
Statystyka opisowa: podstawowe pojęcia
Memory
Szukanie pasujących par.
Kombinatoryka, zbiory, logika
Zbiory
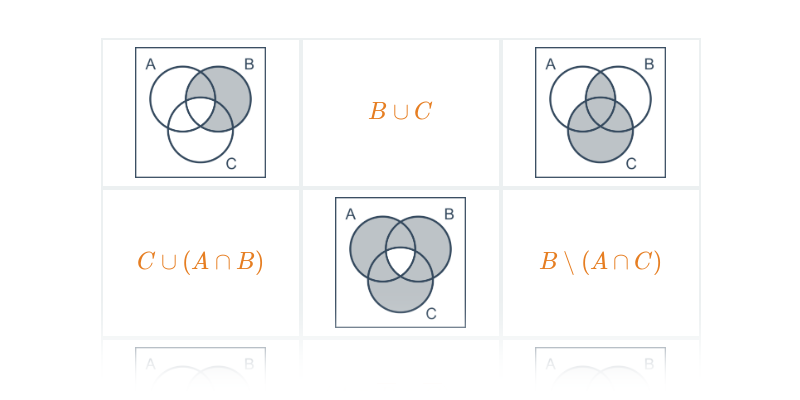
Diagramy Venna
Logika
Logika: pojęcia i oznaczenia
Kombinatoryka
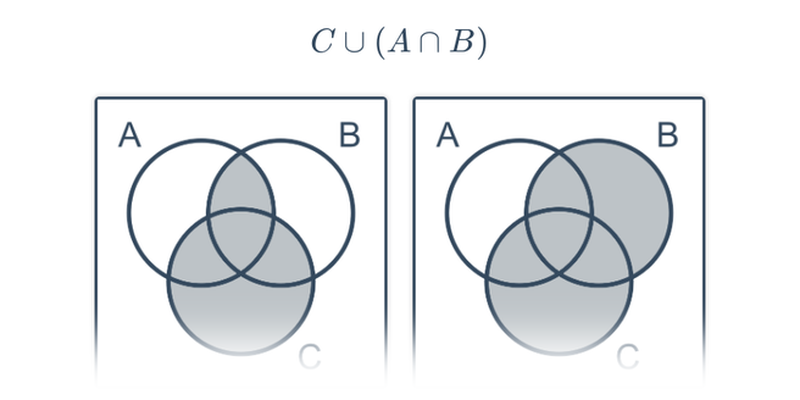
Wpisywanie odpowiedzi
Ćwiczenie, w którym wpisujesz odpowiedź na klawiaturze.
Kombinatoryka, zbiory, logika
Kombinatoryka
Rachunek prawdopodobieństwa
Podstawowe prawdopodobieństwo zdarzenia
Doświadczenia losowe i zdarzenia złożone
Rachunek prawdopodobieństwa: miks przykładów
Prawdopodobieństwo: kostki
Statystyka opisowa
Średnia i mediana
Własności średniej arytmetycznej
Zadania tekstowe
Klasyczne zadania z rozmaitymi przykładami oraz komentarzami do odpowiedzi.
Kombinatoryka, zbiory, logika
Zbiory
Zbiory: miks przykładów
Zadania tekstowe o zbiorach
Kombinatoryka
Permutacje, kombinacje, wariacje
Kombinacje bez powtórzeń
Kombinacje z powtórzeniami
Permutacje i wariacje bez powtórzeń
Permutacje i wariacje z powtórzeniami
Kombinatoryka: różne przykłady
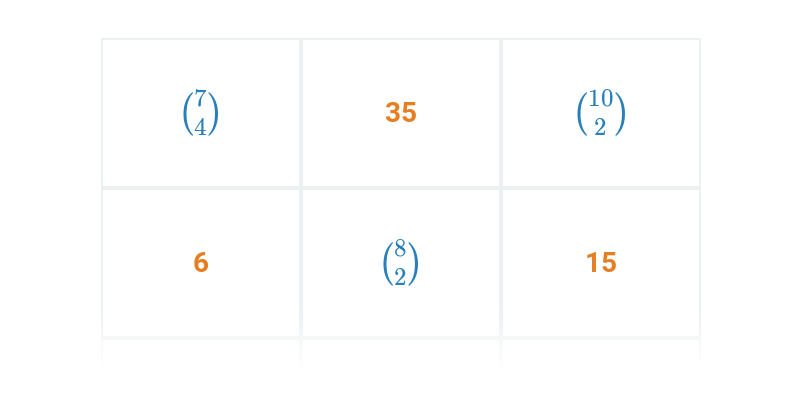
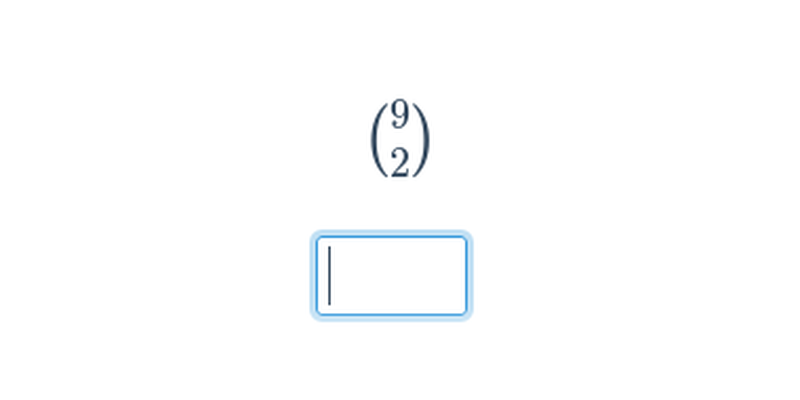
Numeryczna rozgrzewka kombinatoryczna
Rachunek prawdopodobieństwa
Rachunek prawdopodobieństwa: miks przykładów