Świetnie, odznaka %% zdobyta
Funkcje » Decydowanie »
Funkcje
Decydowanie
G7G
kod QR
Kod / krótki adres
Skopiuj kliknięciem.
Ustawienia ćwiczenia
Uwaga, ustawienia dotyczą wyłącznie danego ćwiczenia i przedmiotu.
Własności funkcji
Ze względu na ograniczoną ilość miejsca w tym wyjaśnieniu będziemy rozpatrywać tylko funkcje, których dziedziną są wszystkie liczby rzeczywiste.
Funkcję f nazywamy parzystą, jeżeli dla każdego argumentu x zachodzi warunek f(-x) = f(x). Wykres funkcji parzystej jest symetryczny względem osi y.
Przykłady funkcji parzystych
- f_1(x) = x^2
- f_2(x) = \cos x
- f_3(x) = x^4-3x^2+2
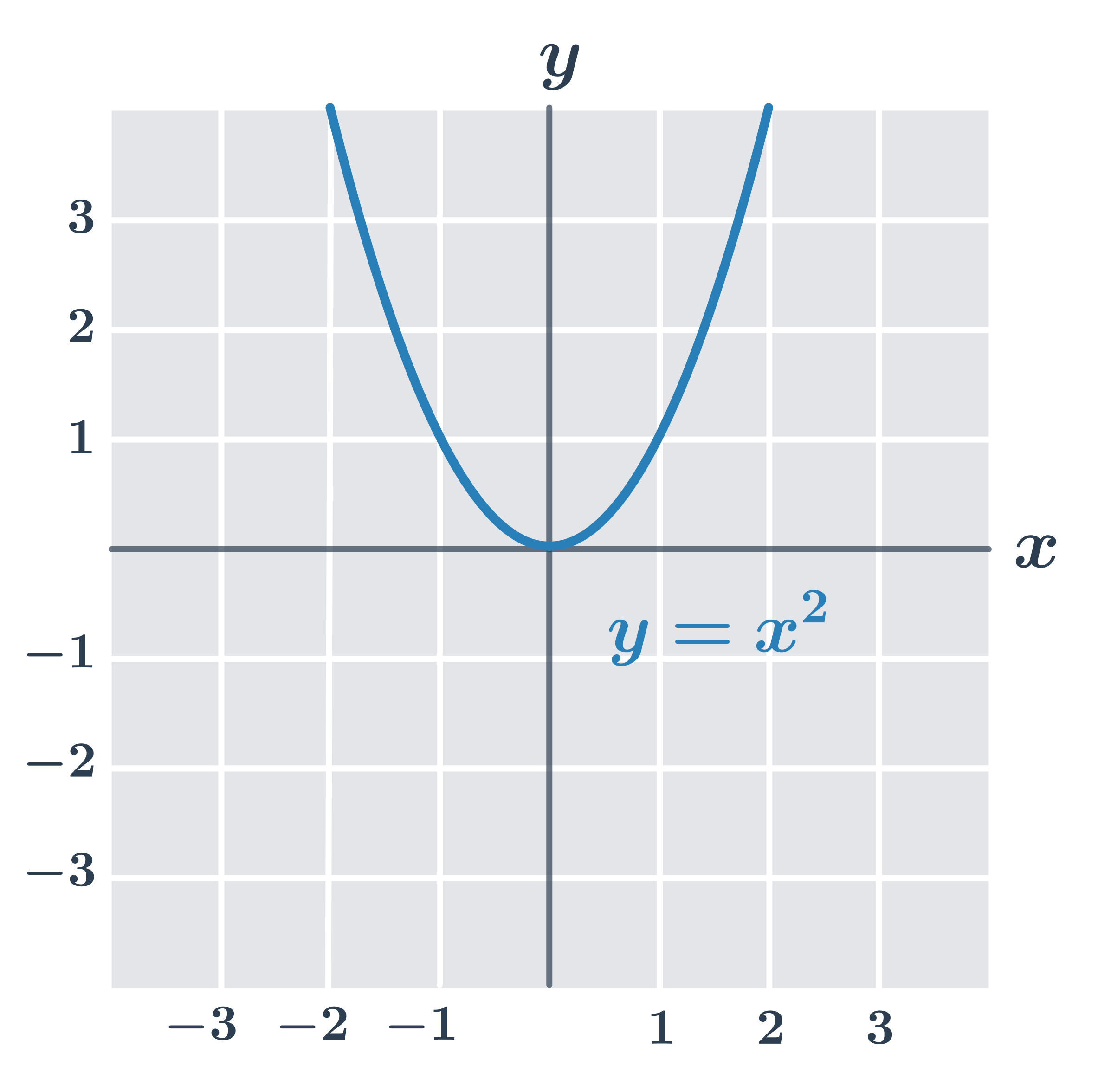
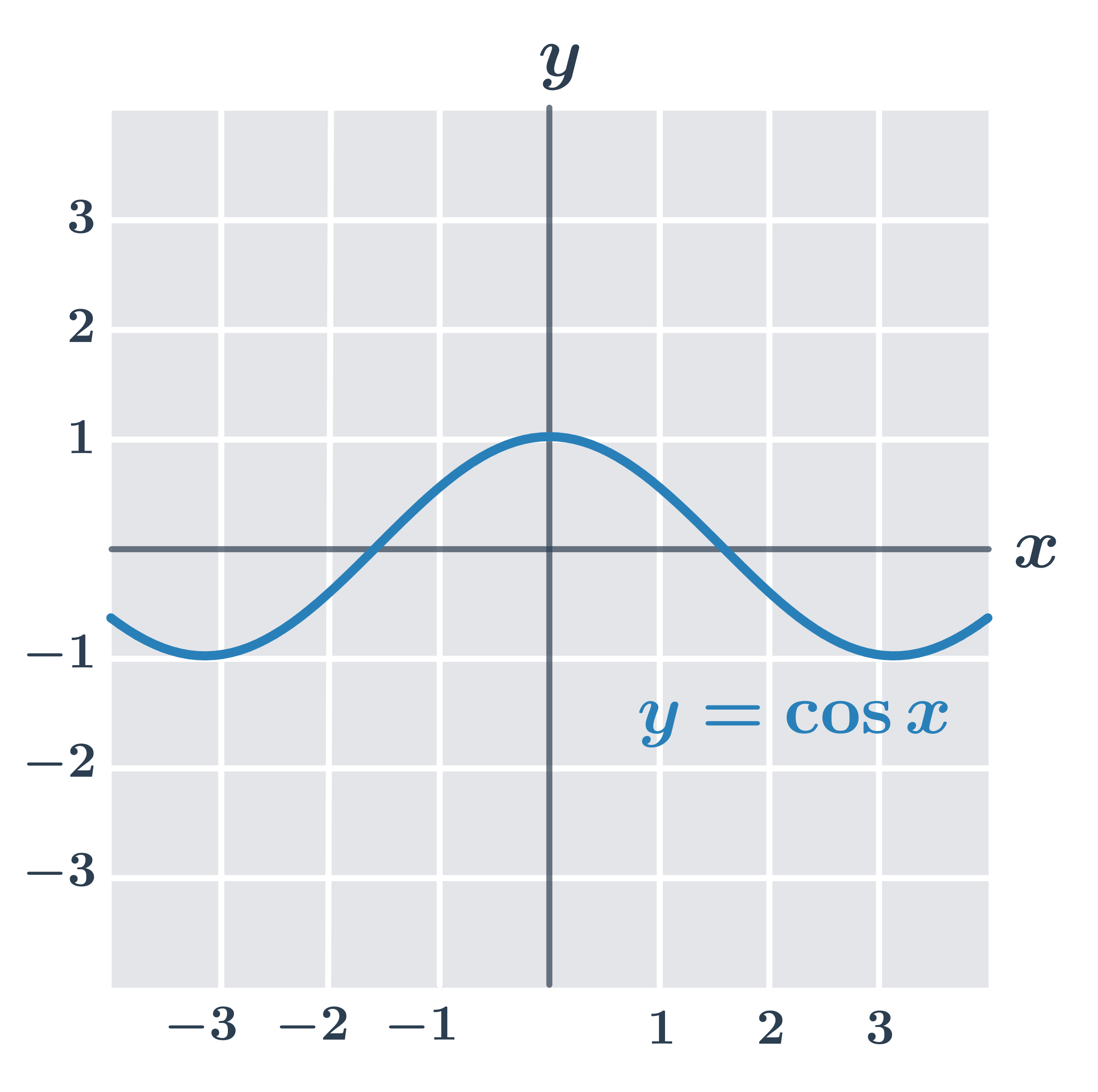
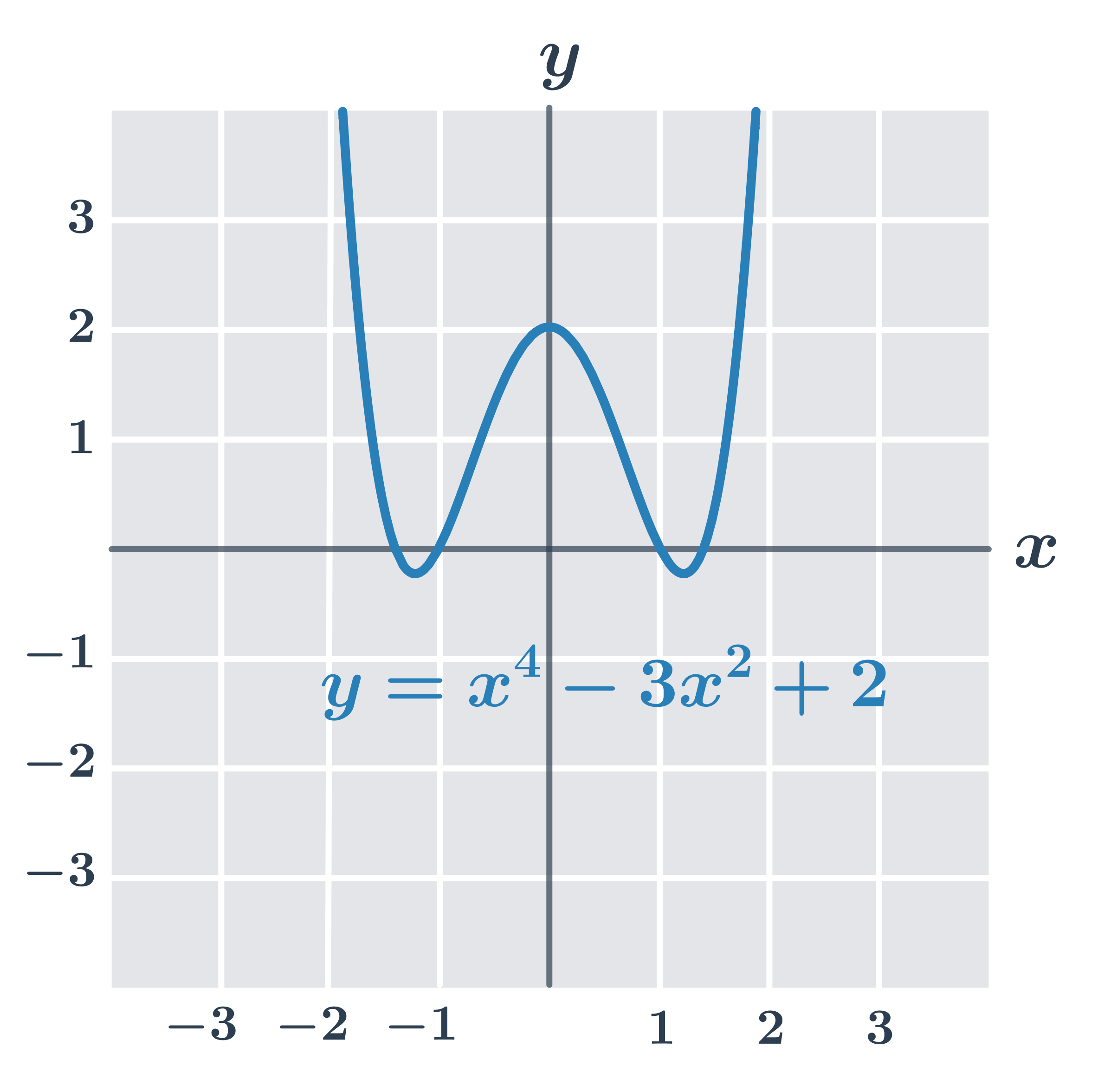
Funkcję f nazywamy nieparzystą, jeżeli dla każdego argumentu x zachodzi warunek f(-x) = -f(x). Wykres funkcji nieparzystej jest symetryczny względem początku układu współrzędnych.
Przykłady funkcji nieparzystych
- f_1(x) = 3x
- f_2(x) = \sin x
- f_3(x) = x^3-2x
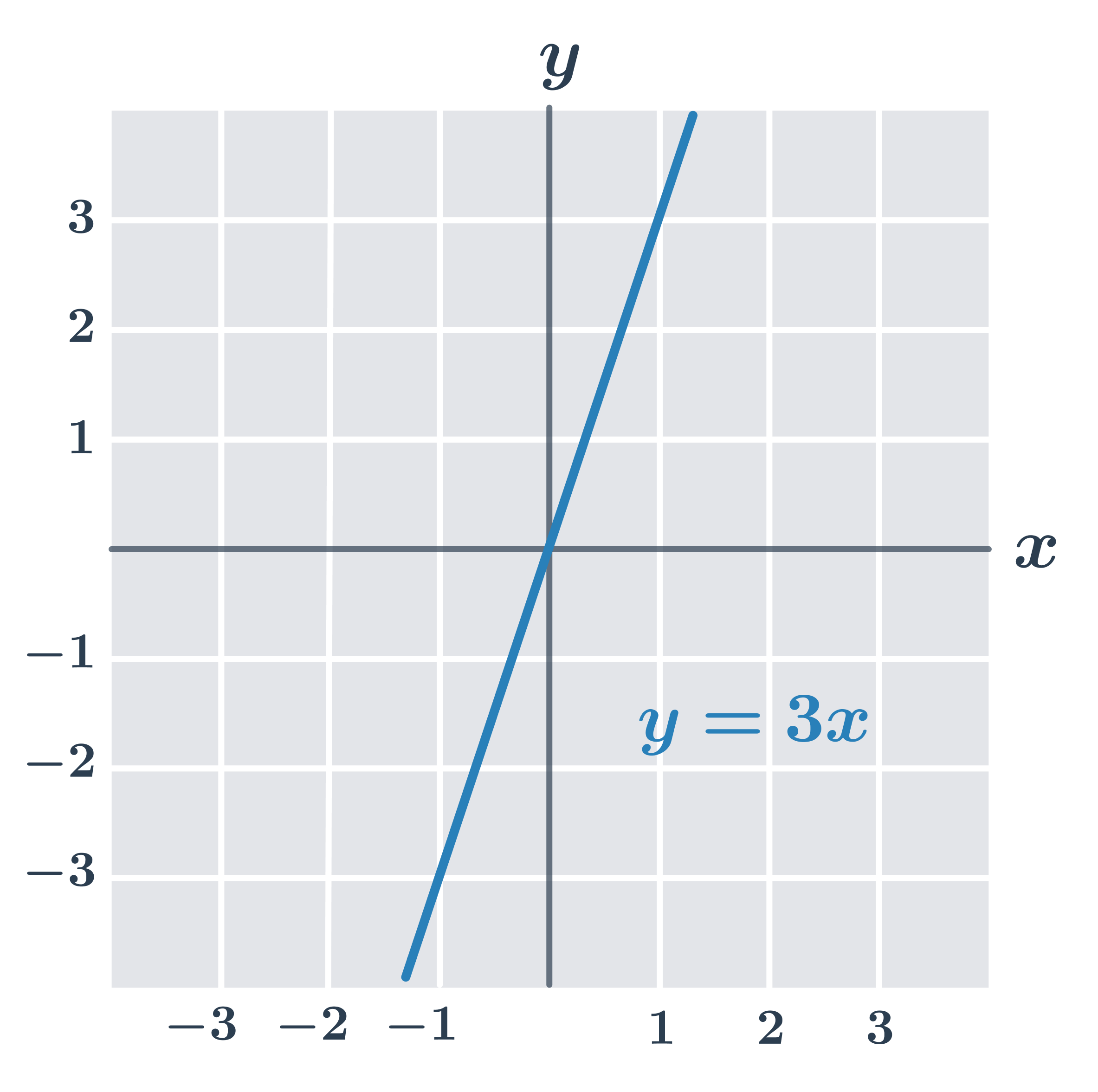
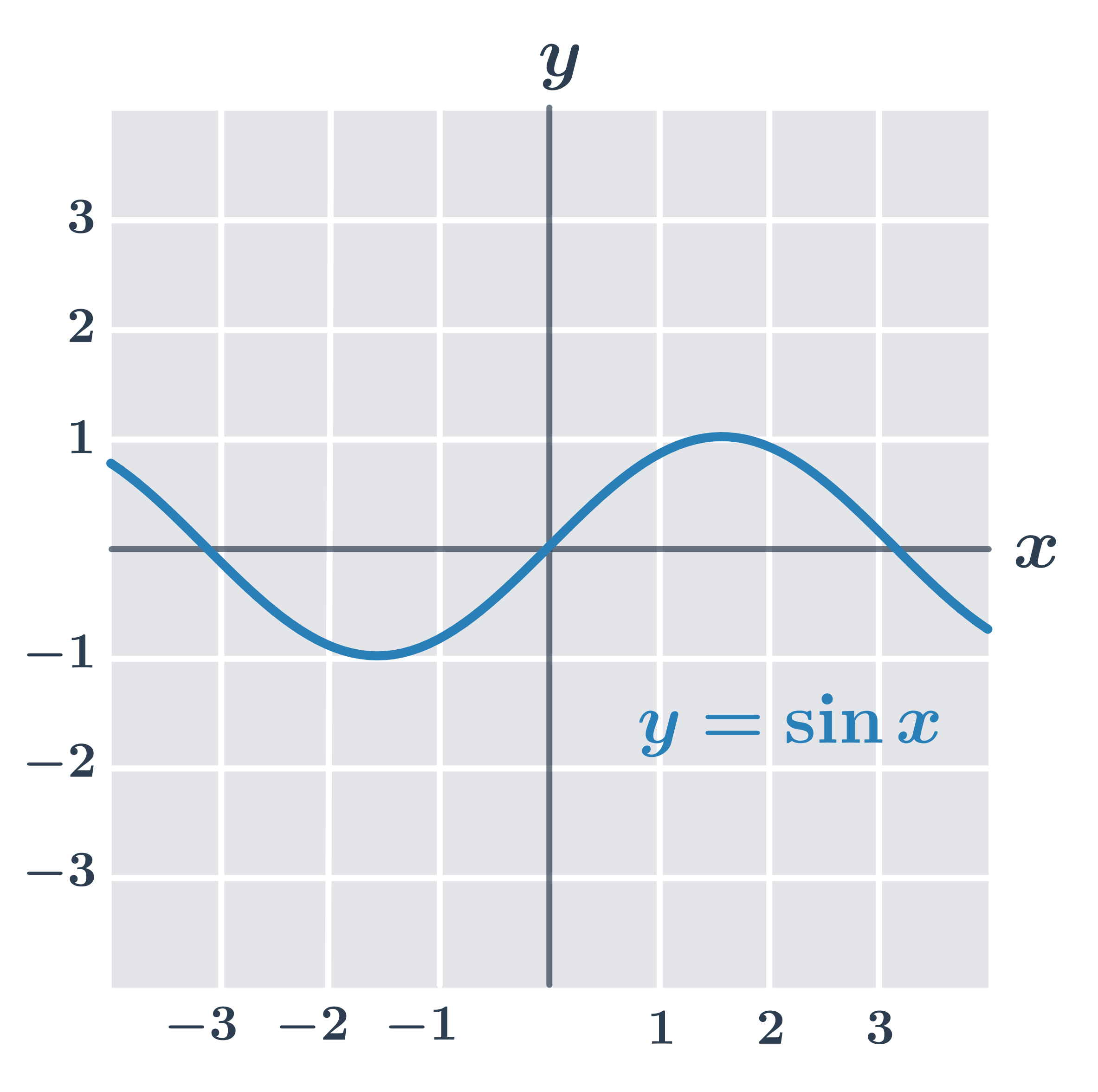
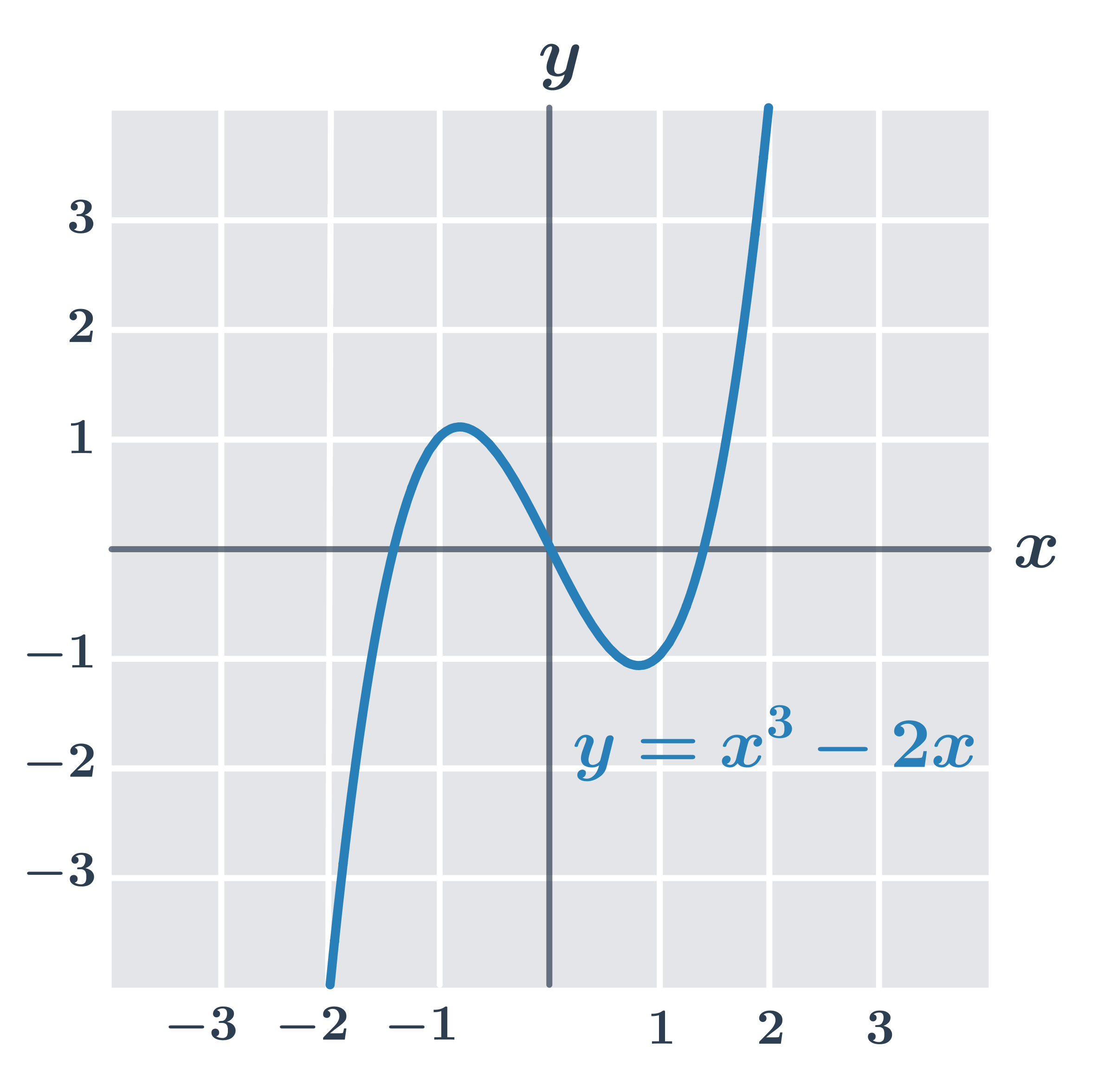
Funkcję f nazywamy okresową, jeżeli istnieje liczba t \neq 0 (zwana okresem funkcji), taka że dla każdego x zachodzi f(x+t)=f(x). Typowymi przykładami funkcji okresowych są funkcje trygonometryczne. Natomiast np. wielomiany nie są funkcjami okresowymi (z wyjątkiem funkcji stałej).
Funkcję f nazywamy ograniczoną z dołu, jeżeli istnieje liczba m, taka że dla każdego x zachodzi f(x) \geq m. Funkcję f nazywamy ograniczoną z góry, jeżeli istnieje liczba M, taka że dla każdego x zachodzi f(x) \leq M. Funkcję f nazywamy ograniczoną, jeżeli jest jednocześnie ograniczona z góry i z dołu.
Przykłady (nie)ograniczonych funkcji
- Funkcja f(x) = \sin x jest ograniczona.
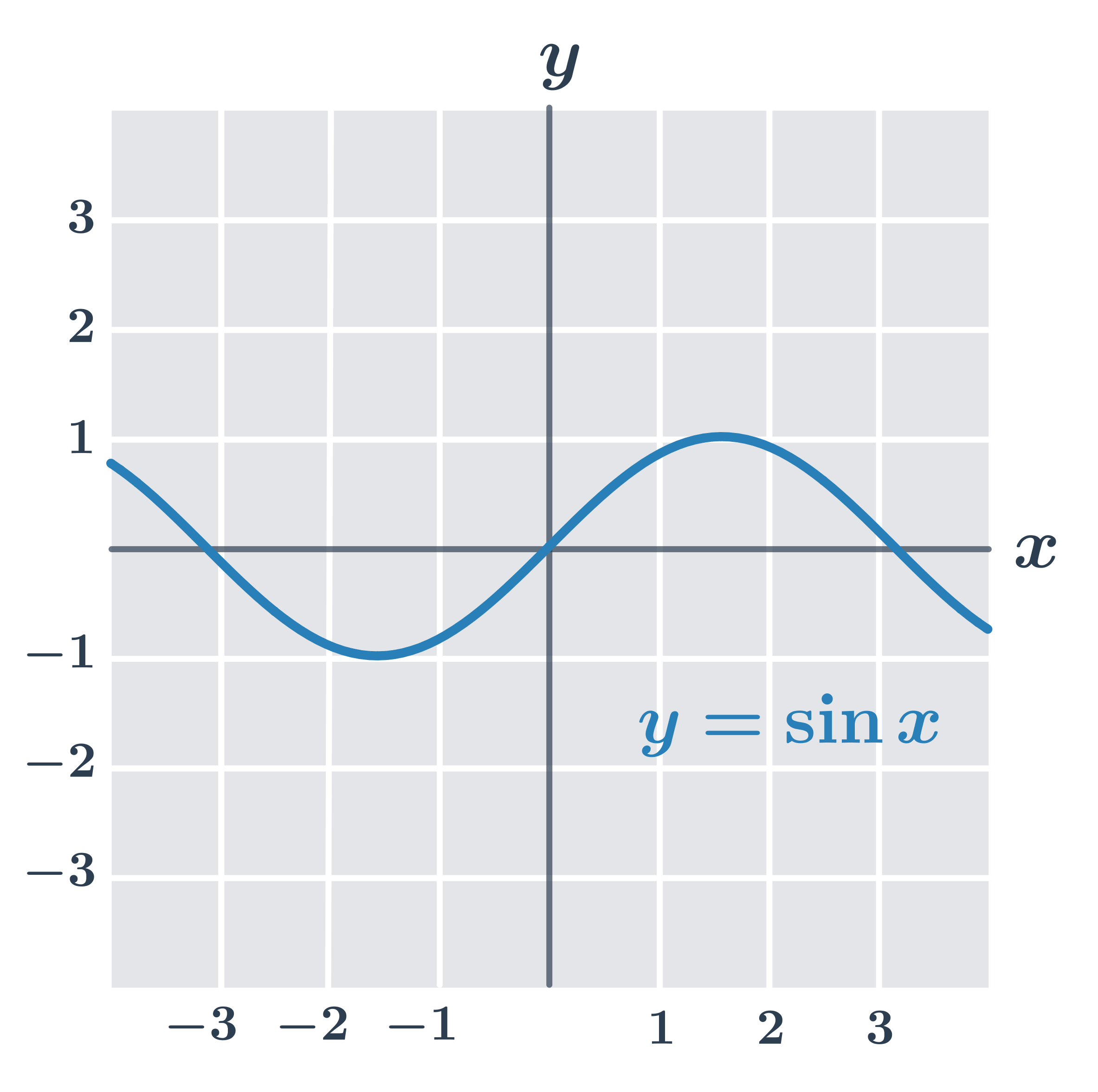
- Funkcja f(x) = x^2 jest ograniczona z dołu (ponieważ \forall x: f(x) \geq 0), ale nie jest ograniczona z góry.
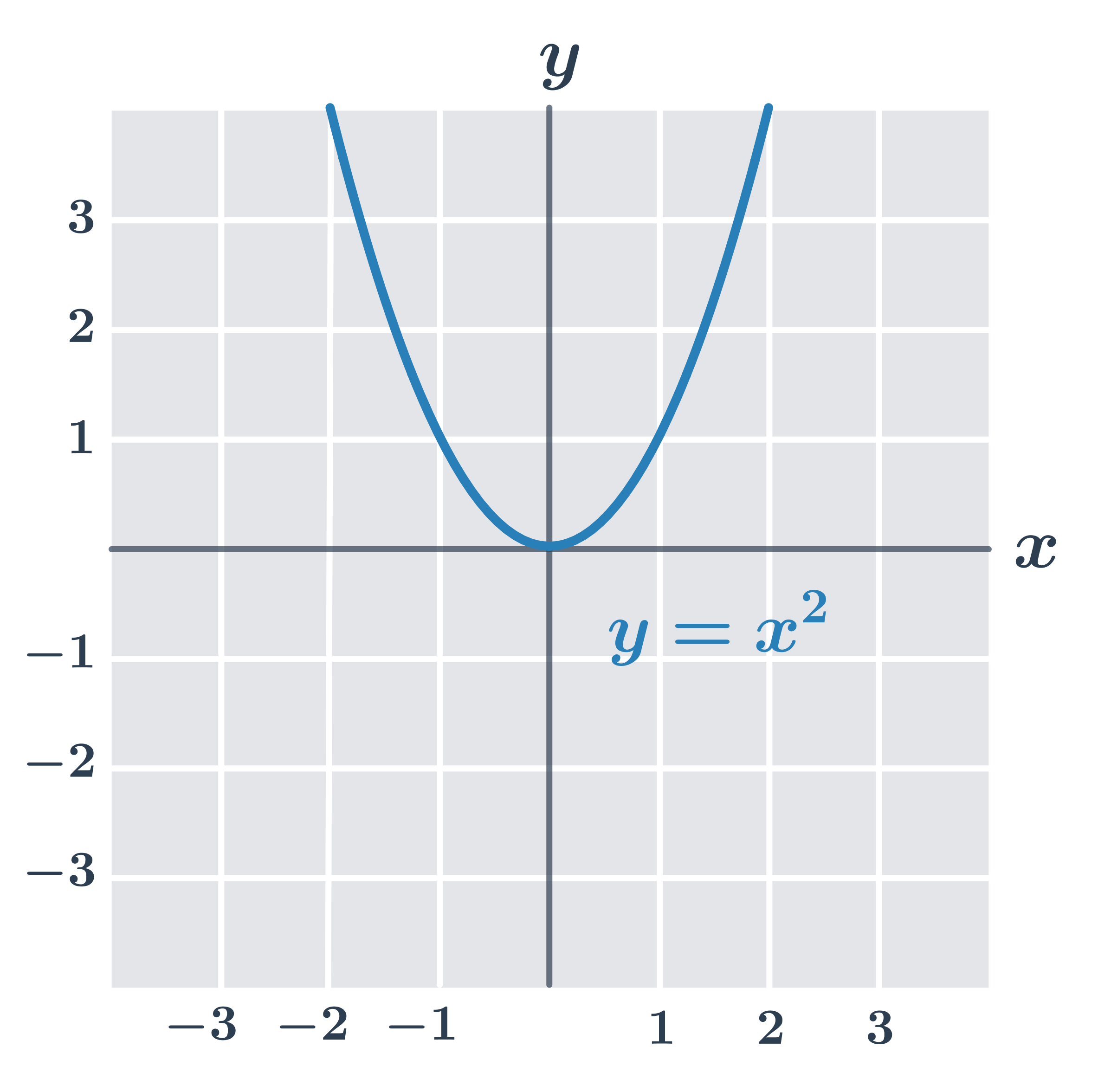
- Funkcja f(x) = 2x nie jest ograniczona ani z góry, ani z dołu.
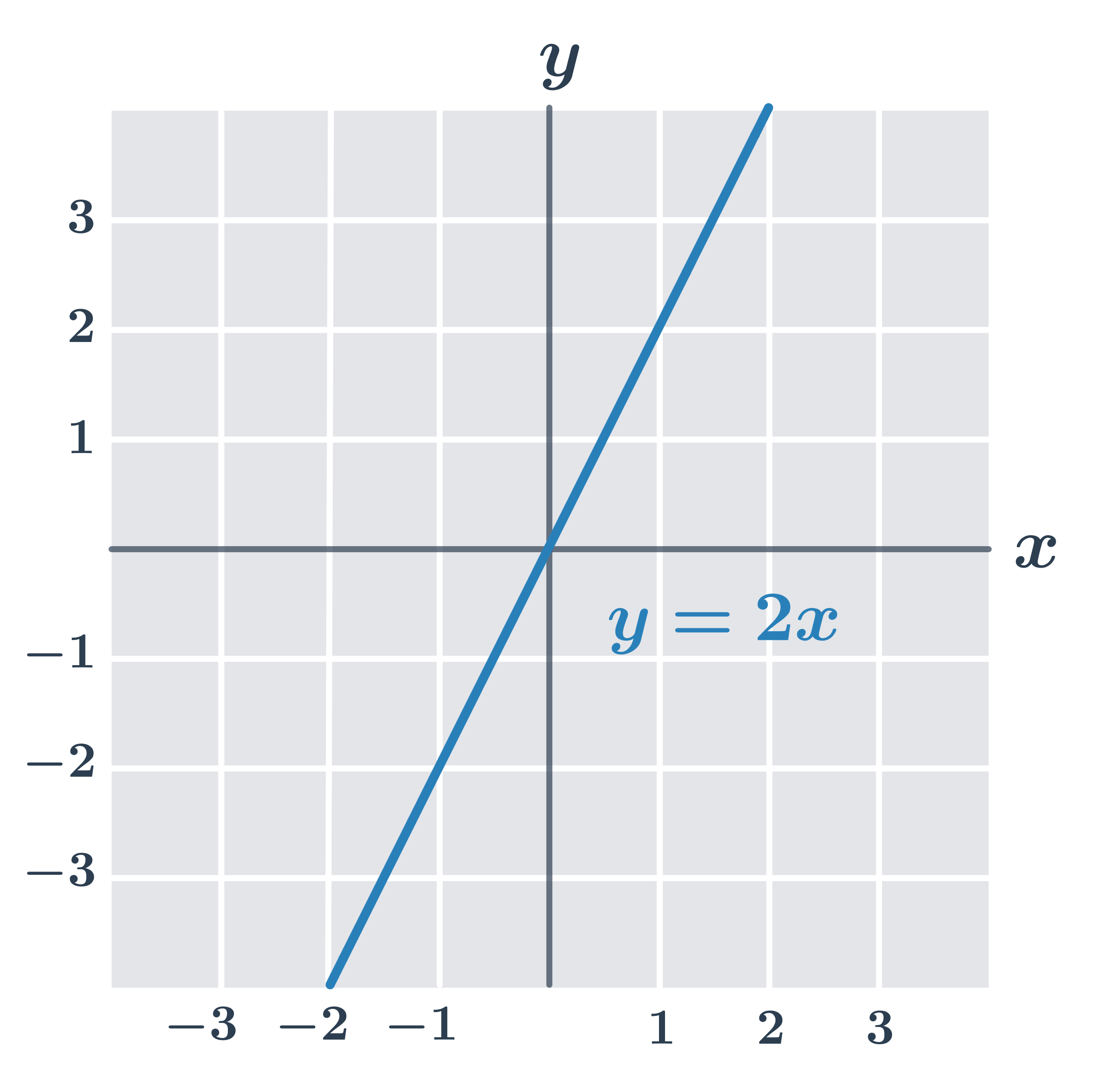
Funkcję f nazywamy różnowartościową, jeżeli dla każdej pary x_1 \neq x_2 zachodzi f(x_1) \neq f(x_2).
Funkcję f nazywamy rosnącą, jeżeli dla każdej pary x_1 \lt x_2 zachodzi f(x_1) \lt f(x_2).
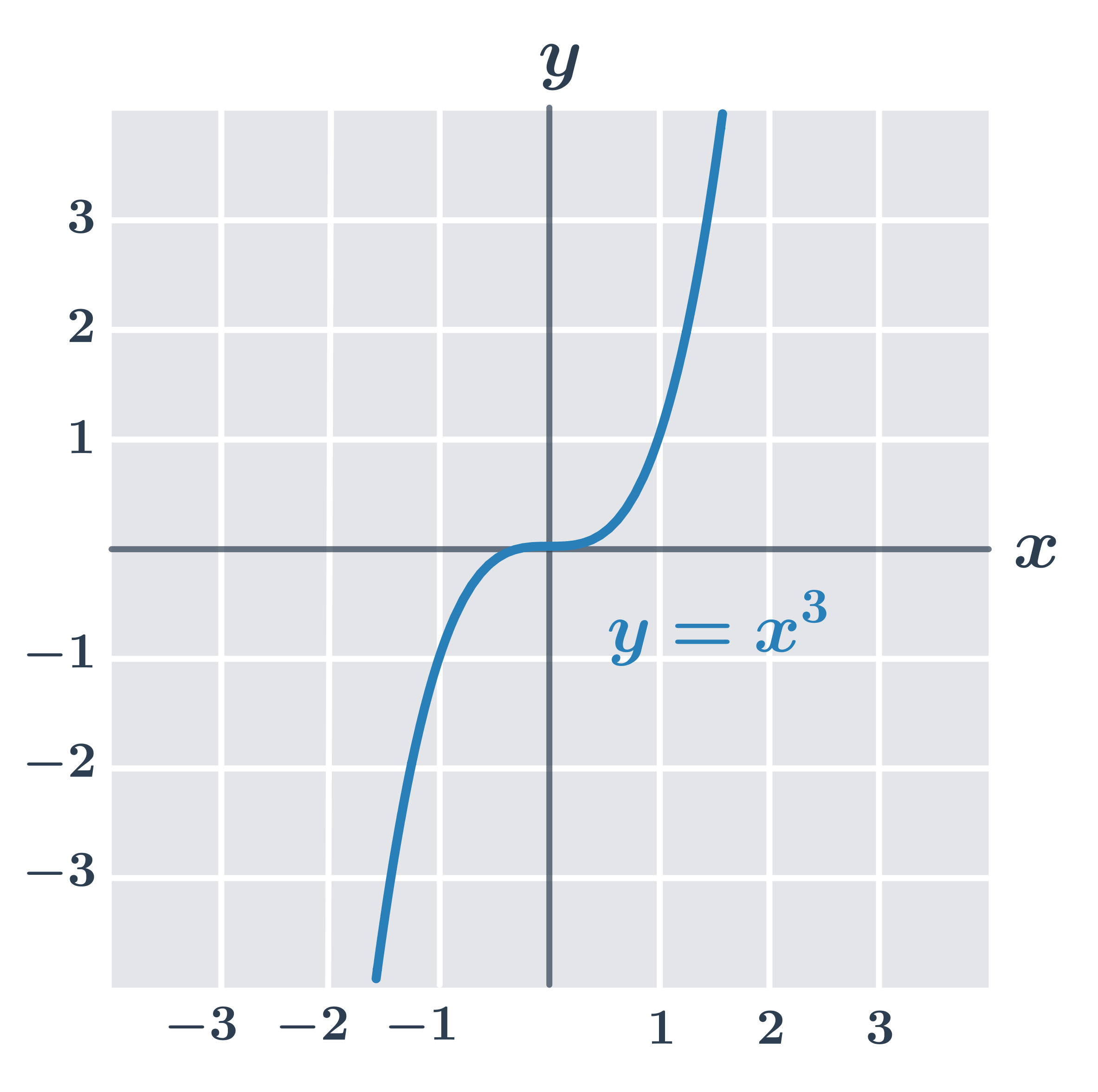
Przykład: funkcja f(x) = x^3
Funkcja f(x)=x^3 o dziedzinie D(f) = \mathbb{R} jest różnowartościowa i rosnąca.
Funkcję f nazywamy malejącą, jeżeli dla każdej pary x_1 \lt x_2 zachodzi f(x_1) \gt f(x_2).
Przykład: funkcja f(x) = \frac{1}{x}
Funkcja f(x)= \frac{1}{x} o dziedzinie D(f) = (-\infty,0) \cup (0,\infty):
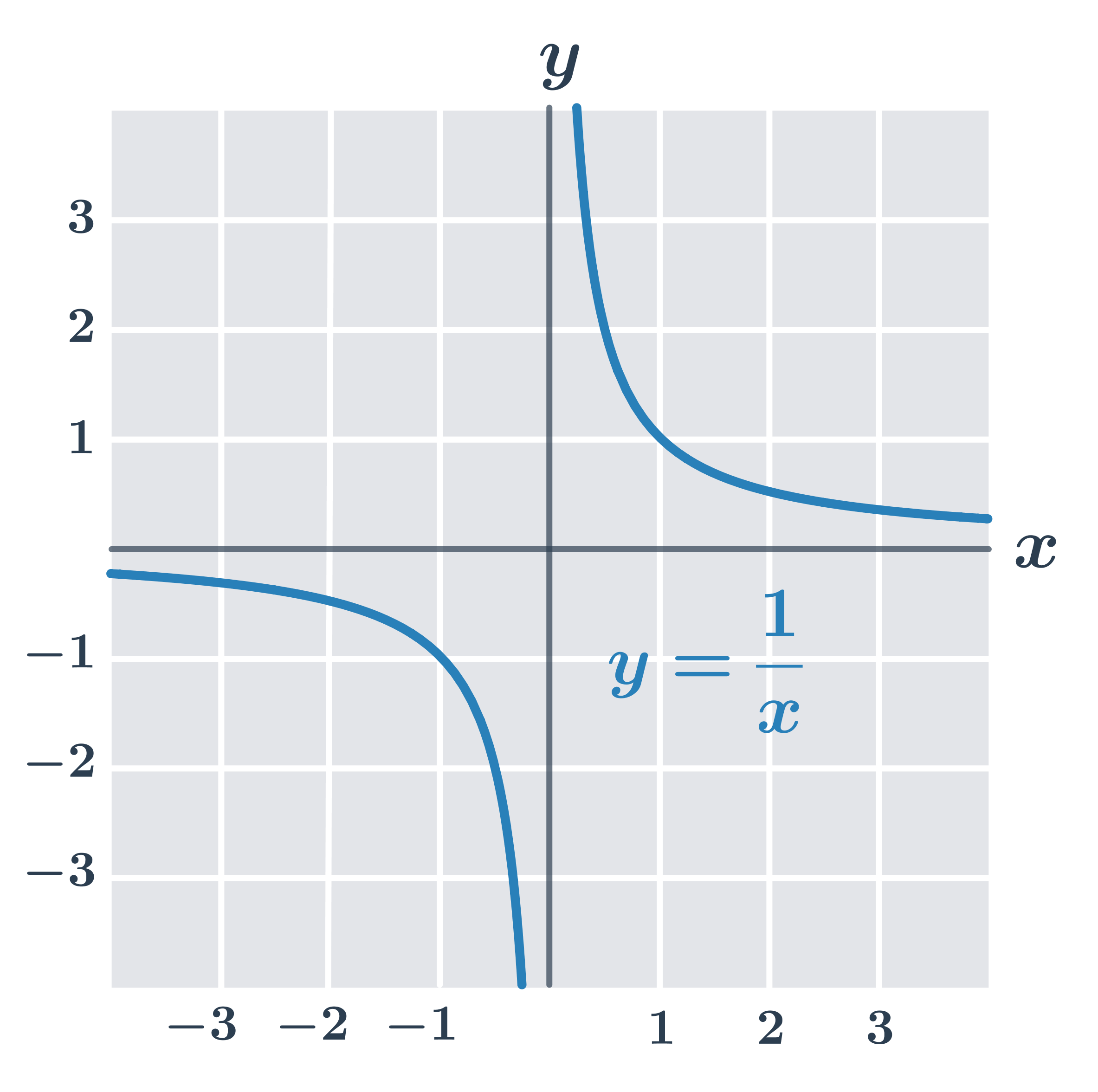
- funkcja maleje na przedziale (-\infty,0)
- funkcja również maleje na przedziale (0,\infty)
- ale funkcja nie jest malejąca na całej dziedzinie D(f), np. -1 \lt 1, lecz f(-1) \lt f(1)
Funkcja f ma maksimum w punkcie x_0, jeżeli dla każdej liczby x \in D(f) zachodzi f(x) \leq f(x_0). Zatem maksimum to punkt, w którym wartość funkcji jest największa (takich punktów może być więcej niż jeden, np. w funkcji sinus).
Funkcja f ma minimum w punkcie x_0, jeżeli dla każdej liczby x \in D(f) zachodzi f(x) \geq f(x_0). Zatem minimum to punkt, w którym wartość funkcji jest najmniejsza (takich punktów również może być więcej niż jeden).
Maksimum i minimum nazywamy ekstremami funkcji.
Przykład: maksimum funkcji f(x)=1-x^2
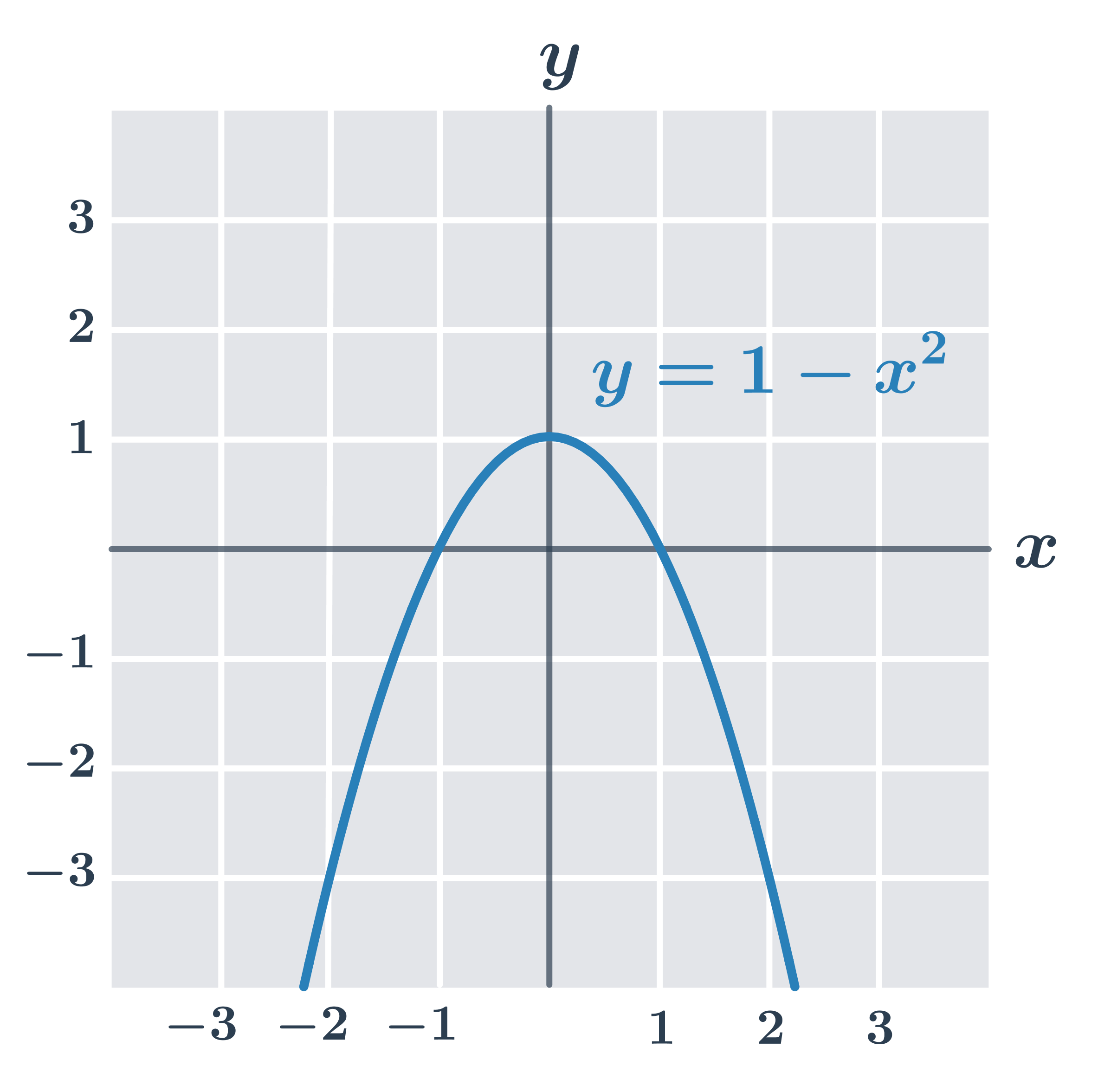
- Funkcja f:y=1-x^2 osiąga najwyższą wartość w punkcie x=0, wynosi f(0)=1, a dla dowolnej liczby rzeczywistej x zachodzi f(x) \leq 1.
- Zatem funkcja osiąga maksimum w punkcie x=0. Funkcja nie ma minimum.
Przykład: minimum funkcji f(x)=(x-1)^2
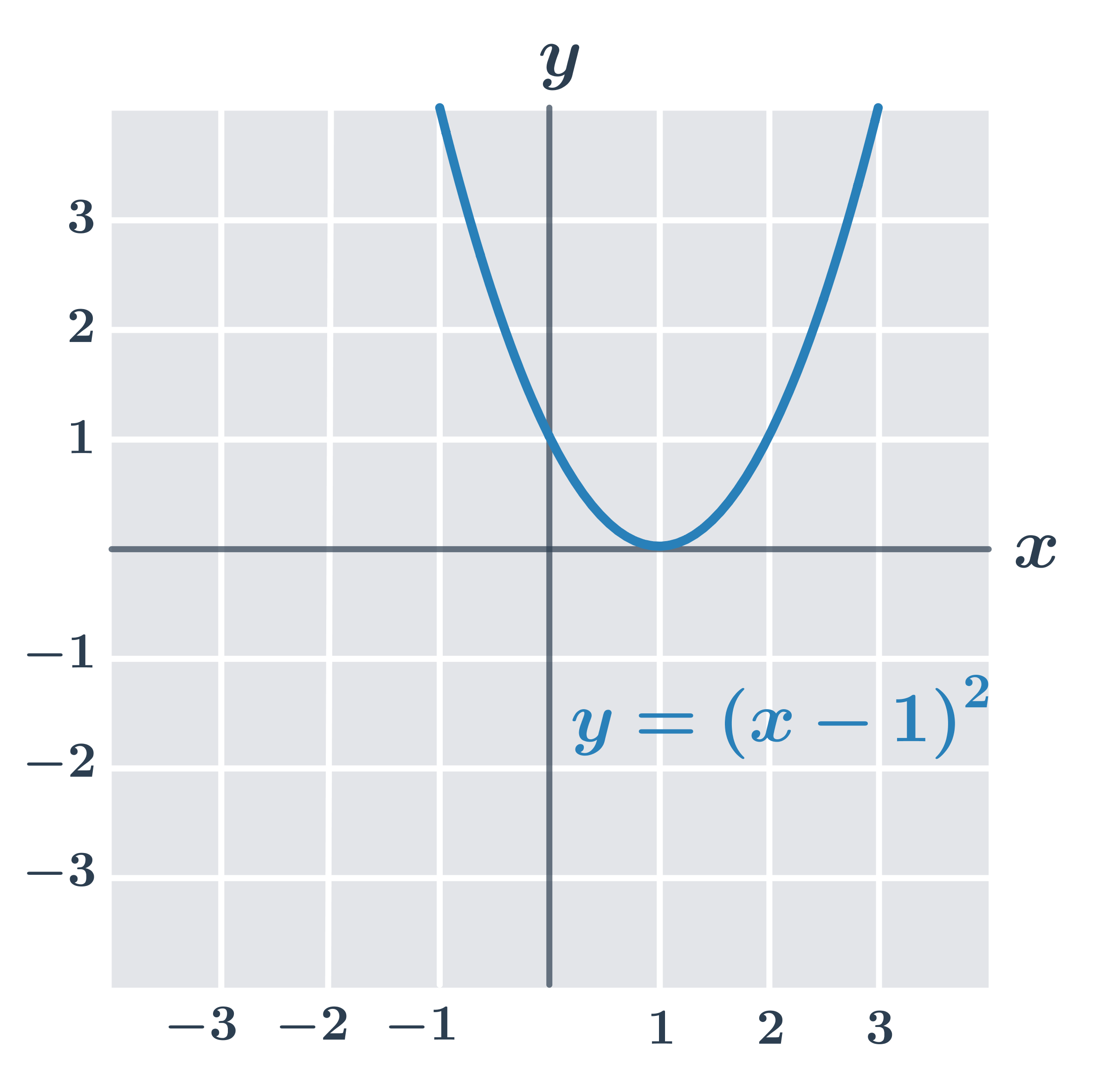
- Funkcja f:y=(x-1)^2 osiąga najniższą wartość w punkcie x=1, wynosi f(1) = 0, a dla dowolnej liczby rzeczywistej x zachodzi f(x) \geq 0.
- Zatem funkcja ma minimum w punkci x=1. Funkcja nie ma maksimum.
Własności funkcji (trudne)
Od tego momentu przykłady mogą się potwarzać.