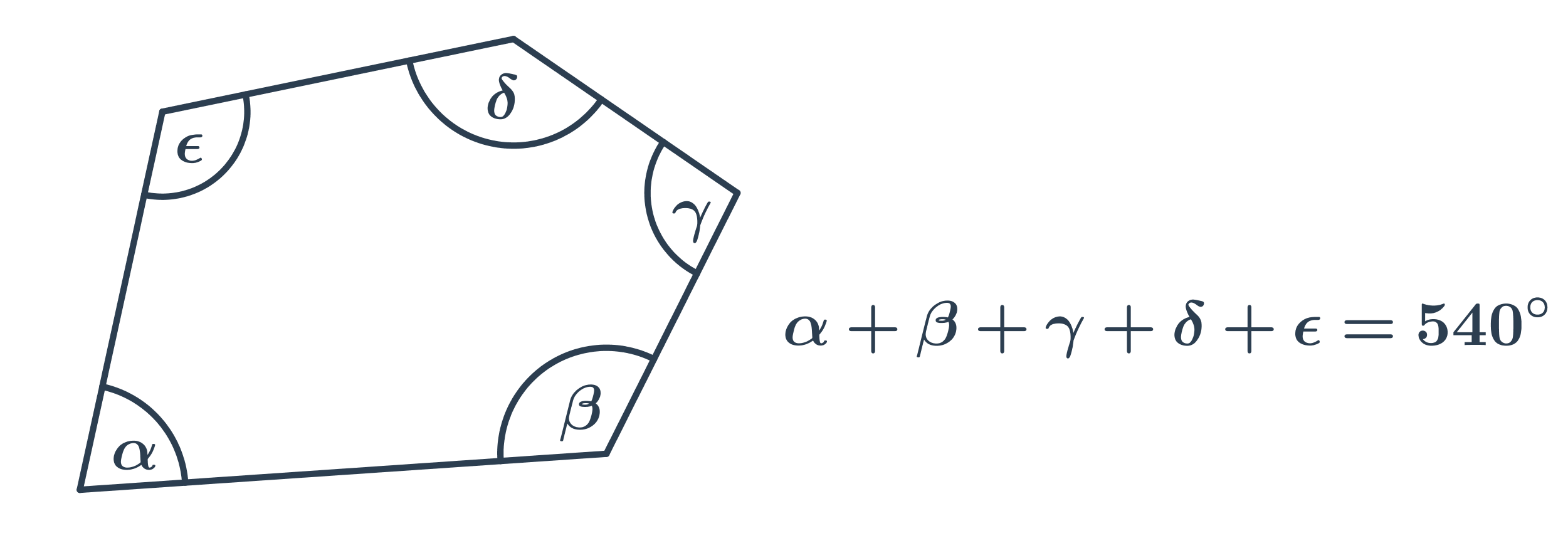Świetnie, odznaka %% zdobyta
Geometria » Wpisywanie odpowiedzi »
Geometria
Wpisywanie odpowiedzi
Dostęp bez ograniczeńKorzystasz z platformy z limitem dziennym na liczbę odpowiedzi. Aby zwiększyć limit lub uzyskać dostęp do konta z licencją, zaloguj się.
Zaloguj się
E2Jkod QR
Kod / krótki adres
Skopiuj kliknięciem.
Kąty i wielokąty
Suma miar kątów wewnętrzych w wielokącie o n bokach (czyli n-kącie) wynosi 180^\circ\cdot(n-2). Na przykład suma miar kątów wewnętrzych w pięciokącie wynosi 180^\circ(5-2)=540^\circ. Każdy kąt wewnętrzy może mieć inną miarę.
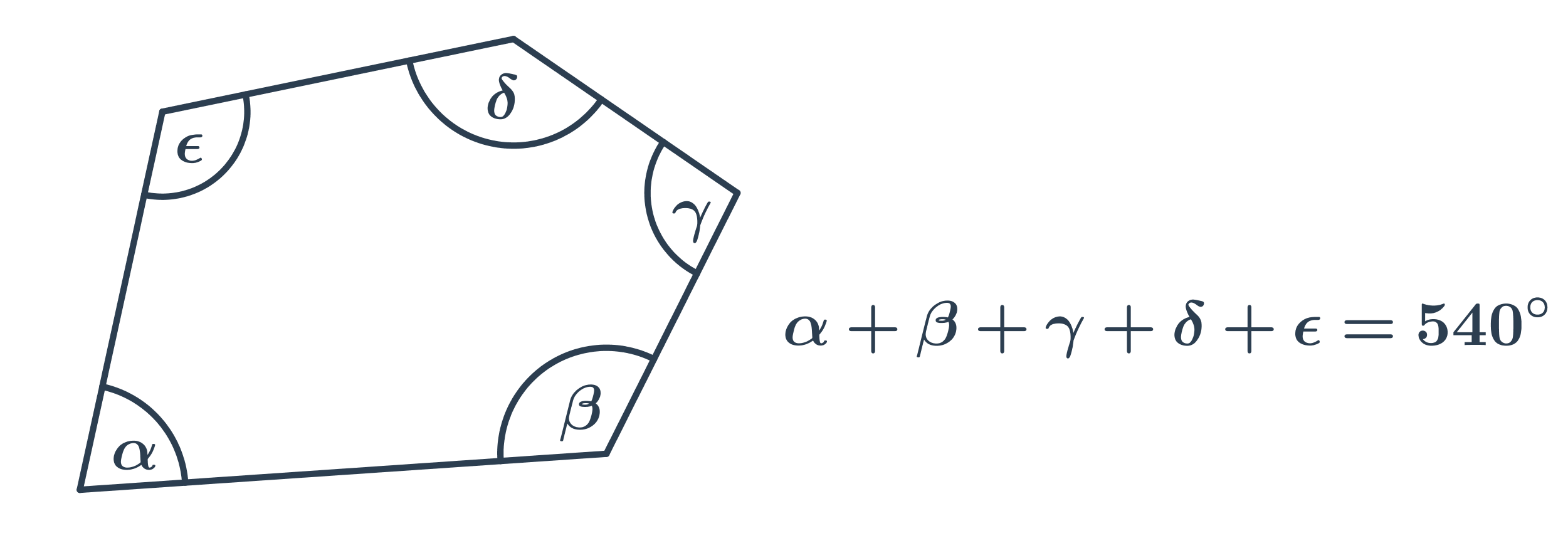
Wielokąty foremne
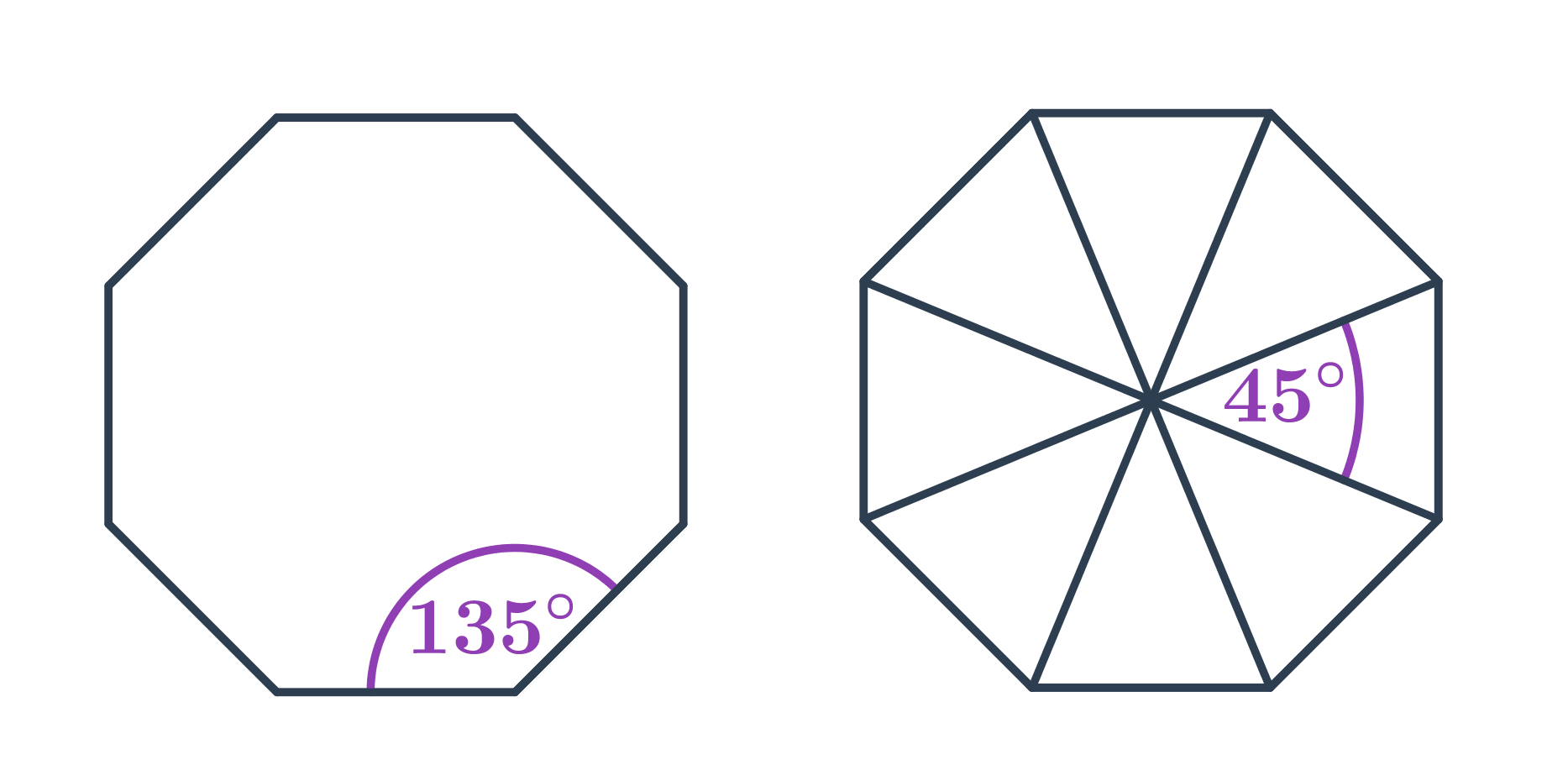
- Każdy kąt wewnętrzny w wielokącie foremnym o n wierzchołkach ma miarę 180^\circ\cdot\frac{n-2}{n}. Na przykład w ośmiokącie foremnym każdy kąt wewnętrzny ma miarę 180^\circ\cdot\frac{8-2}{6}=135^\circ.
- Miara kąta środkowego w n-kącie foremnym wynosi \frac{360^\circ}{n}. Na przykład w ośmiokącie foremnym każdy kąt środkowy ma miarę \frac{360^\circ}{8}=45^\circ.
Do obliczenia miary nieznanego kąta w wielokącie można skorzystać również z kątów wierzchołkowych i przyległych.
Przykład: Oblicz miarę kąta
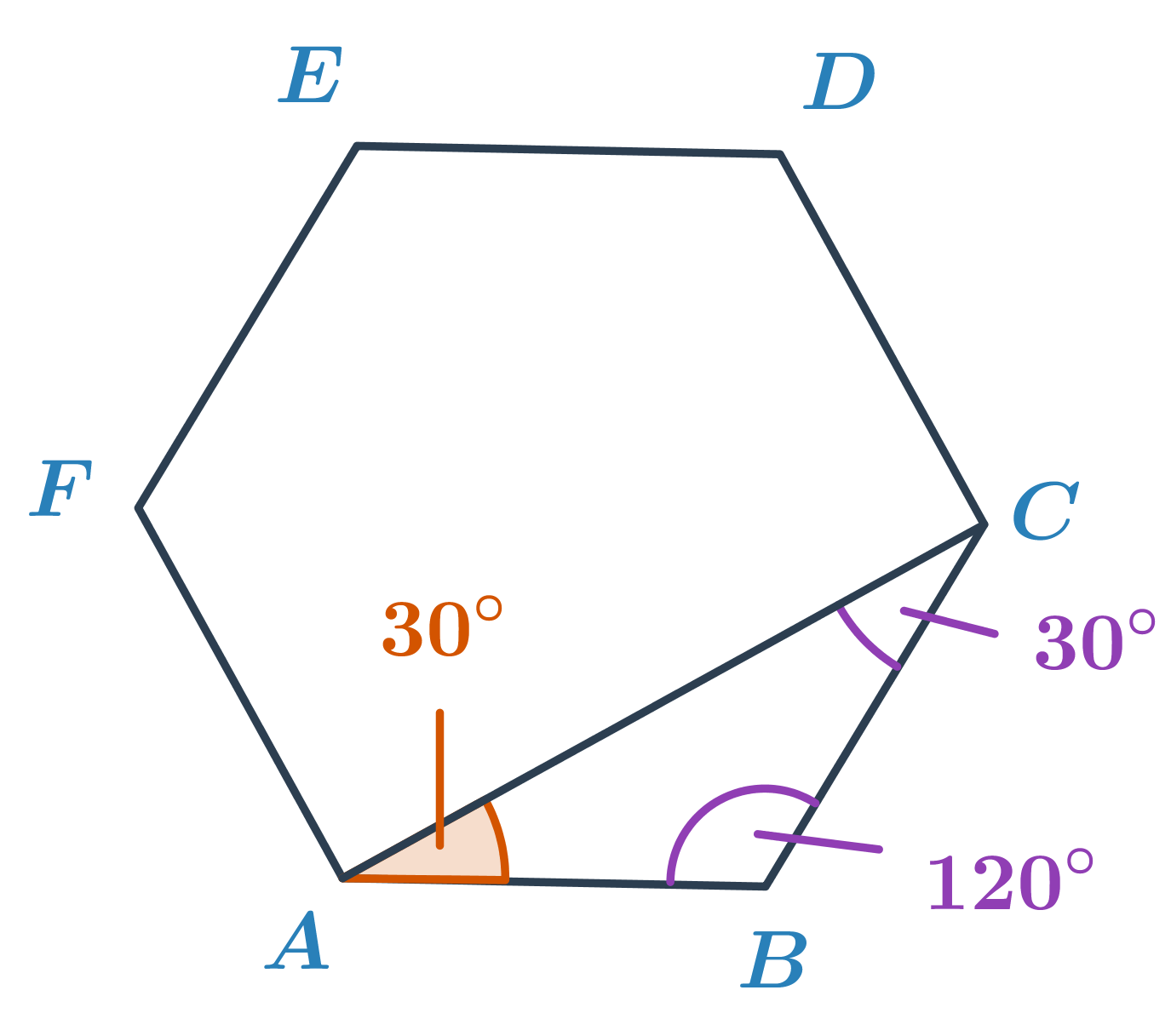
Oblicz miarę kąta zaznaczanego na pomarańczowo w sześciokącie foremnym ABCDEF.
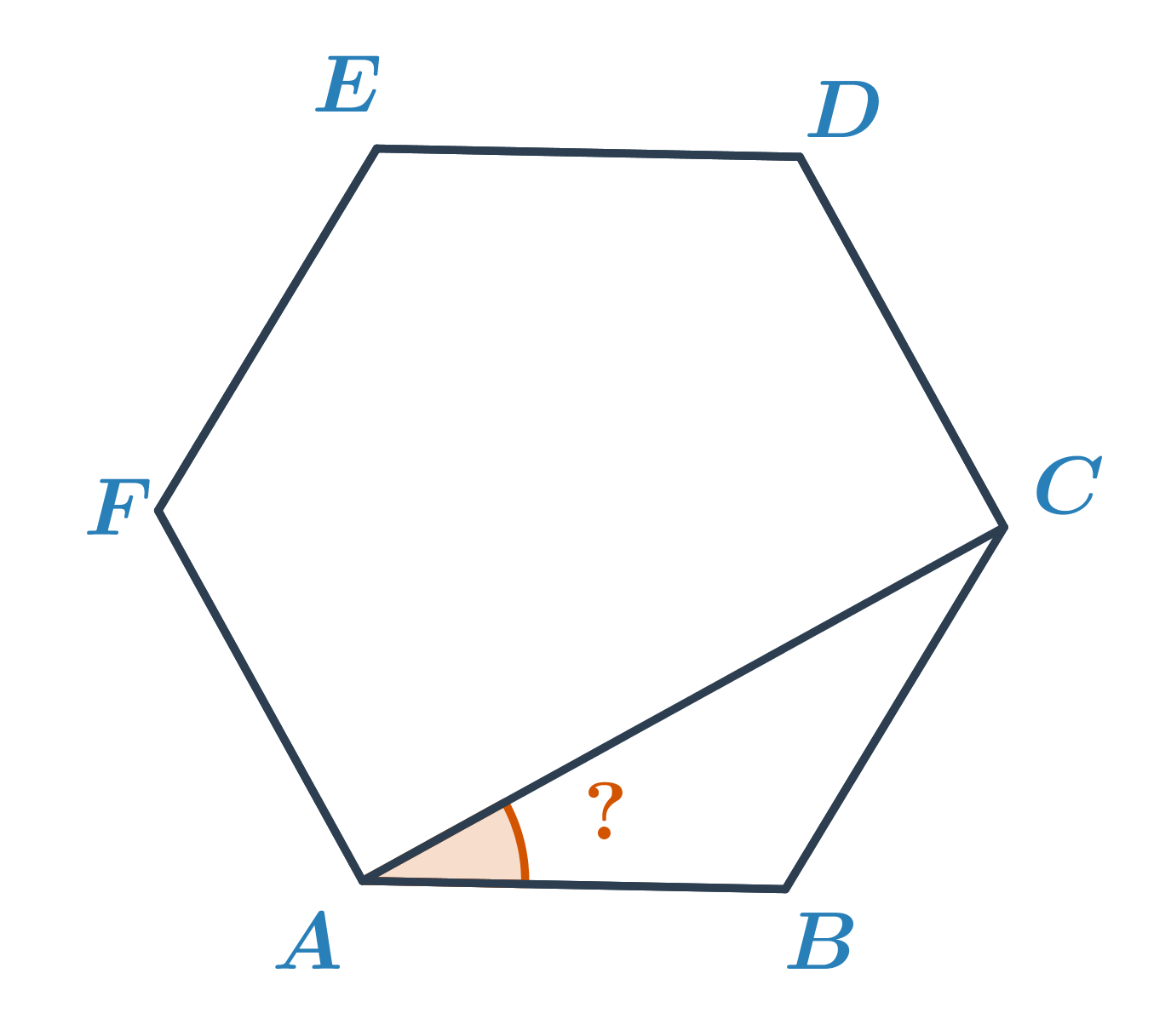
W sześciokącie foremnym każdy kąt ma taką samą miarę, wynoszącą 180^\circ\cdot\frac{6-2}{6}=120^\circ. Zatem kąt ABC będzie miał miarę 120^\circ. Trójkąt ABC jest trójkątem równoramiennym, a kąty przy wierzchołkach A i C są takie same. Ich miara wynosi (180^\circ-120^\circ):2=30^\circ.
Kąty i wielokąty (średnie)
