
Wartości funkcji trygonometrycznych

Często używane wartości funkcji trygonometrycznych ilustruje poniższy rysunek okręgu jednostkowego:
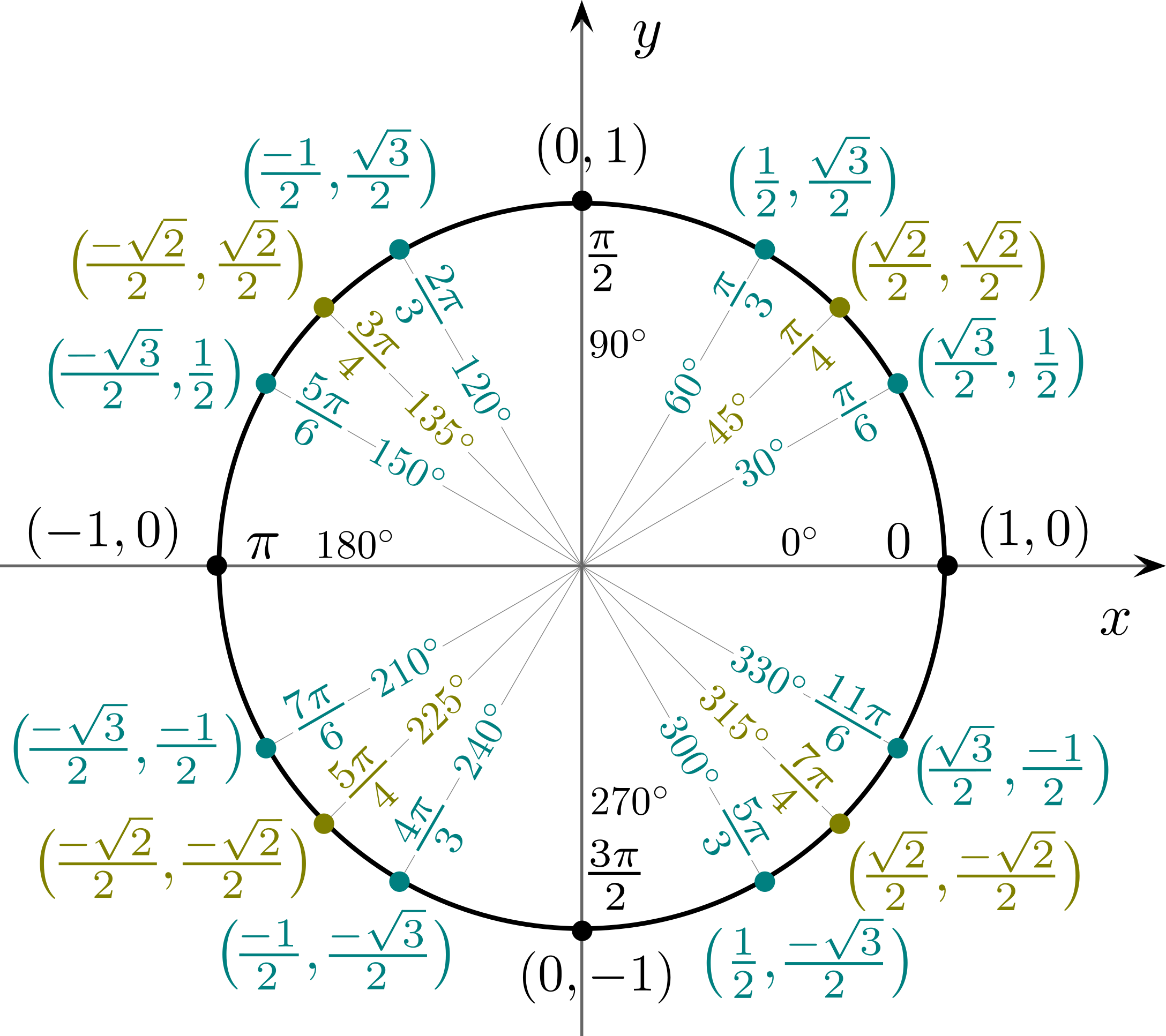
Półprosta, która tworzy kąt \alpha z dodatnią częścią osi x i zaczyna się w początku układu współrzędnych, przecina okrąg jednostkowy w punkcie o współrzędnych [\cos \alpha; \sin \alpha], czyli:
- współrzędna x punktu odpowiada wartości \cos danego kąta,
- współrzędna y punktu odpowiada wartości \sin danego kąta.
Przykład: sinus i cosinus kąta 30°
Półprosta, która tworzy z dodatnią częścią osi x kąt 30° (czyli \frac{\pi}{6} radiana), przecina okrąg jednostkowy w punkcie [\frac{\sqrt{3}}{2}; \frac12]. Zatem mamy:
- \cos 30^{\circ} = \frac{\sqrt{3}}{2}
- \sin 30^{\circ} = \frac12
Przykład: tangens kąta 150°
Półprosta, która tworzy z dodatnią częścią osi x kąt 150° (czyli \frac{5\pi}{6} radiana), przecina okrąg jednostkowy w punkcie [-\frac{\sqrt{3}}{2}; \frac12]. Zatem mamy:
- \cos 150^{\circ} = -\frac{\sqrt{3}}{2}
- \sin 150^{\circ} = \frac12
- obliczamy \tan 150^{\circ} jako iloraz \frac{\sin 150^{\circ}}{\cos 150^{\circ} }
- \tan 150^{\circ} = \frac12 : \left(-\frac{\sqrt{3}}{2}\right) = \frac12 \cdot \left(-\frac{2}{\sqrt{3}}\right) = -\frac{1}{\sqrt{3}} = -\frac{\sqrt{3}}{3}
Zamknij












