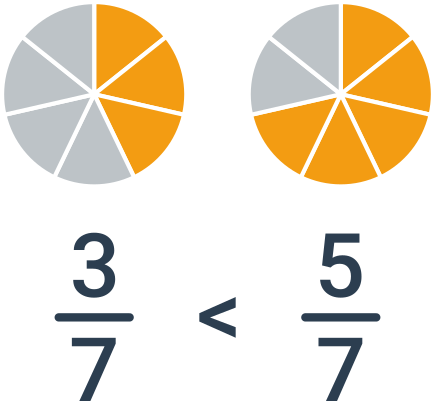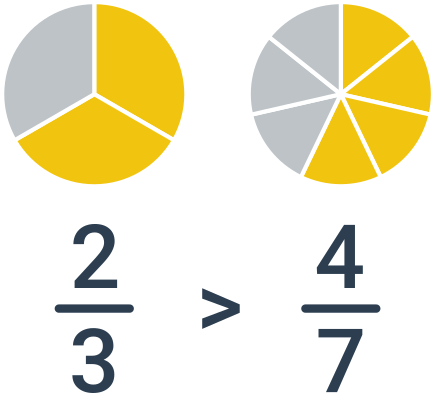Porównywanie ułamków zwykłych

Zanim przystąpimy do porównywania ułamków zwykłych, przypomnijmy sobie, gdzie jest licznik („na górze“), a gdzie mianownik („na dole“). Czyli w ułamku \frac{3}{7} licznikiem będzie liczba 3, a mianownikiem liczba 7.
Porównywanie ułamków o tym samym mianowniku
Porównywanie ułamków o jednakowych mianownikach jest proste — wystarczy porównać liczniki. Weźmy na przykład ułamki \frac{3}{7} i \frac{5}{7}. Liczba 5 jest większa od liczby 3, zatem drugi ułamek będzie większy. Innymi słowy, jeśli podzielimy pizzę na siedem kawałków, to osoba, która zje pięć kawałków, zje więcej od osoby, która zje trzy kawałki.
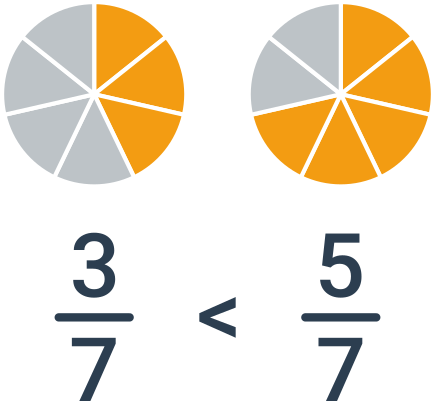
Porównywanie ułamków o tym samym liczniku
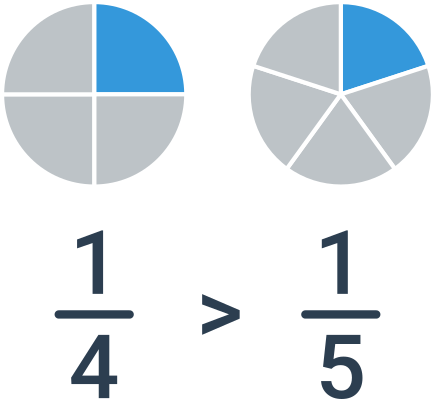
Jeśli ułamki mają ten sam licznik, wystarczy porównać mianowniki. Obowiązuje zasada, że im mniejszy mianownik, tym większy ułamek. Weźmy na przykład ułamki \frac{1}{4} i \frac{1}{5}. Jedna czwarta jest większa od jednej piątej. Innymi słowy, jeśli mam dostać tylko jeden kawałek pizzy, to będzie on większy, jeżeli podzielimy pizzę na 4 kawałki, niż gdybyśmy podzielili ją na pięć kawałków.
Różne mianowniki i liczniki
W takiej sytuacji najpierw musimy sprowadzić ułamki do wspólnego mianownika, a dopiero potem porównać liczniki. Na przykład: porównujemy ułamki \frac{2}{3} i \frac{4}{7}. Najmniejszy wspólny mianownik to 21, po rozszerzeniu otrzymujemy ułamki \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} i \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Ponieważ 14 \gt 12, większy jest pierwszy ułamek, czyli \frac{2}{3}.
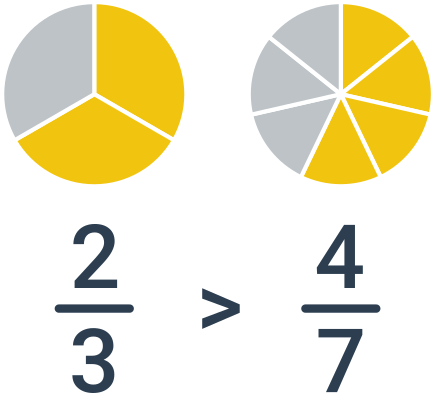
Porównywanie bez obliczeń
Nierzadko możemy porównać ułamki bez wykonywania dokładnych obliczeń, musimy tylko dobrze je sobie wyobrazić lub porównać z odpowiednią wartością „pomiędzy”.
Ułamki \frac{2}{3} i \frac{7}{6}. Pierwszy ułamek jest mniejszy niż 1, drugi ułamek jest większy niż 1. Zatem \frac{2}{3} \lt \frac{7}{6}.
Ułamki \frac{1}{3} i \frac{4}{5}. Pierwszy ułamek na pewno jest mniejszy niż jedna druga, drugi jest dużo większy niż jedna druga. Zatem \frac{1}{3} \lt \frac{4}{5}.
Zamknij