Filtruj według klasy
Objętość i pole powierzchni całkowitej
Objętość bryły jest miarą „ilości” miejsca zajmowanego przez bryłę w przestrzeni. Możemy ją sobie wyobrazić jako ilość wody, której potrzebowalibyśmy, gdybyśmy chcieli „napełnić” bryłę. Objętość wyrażamy w jednostkach objętości.
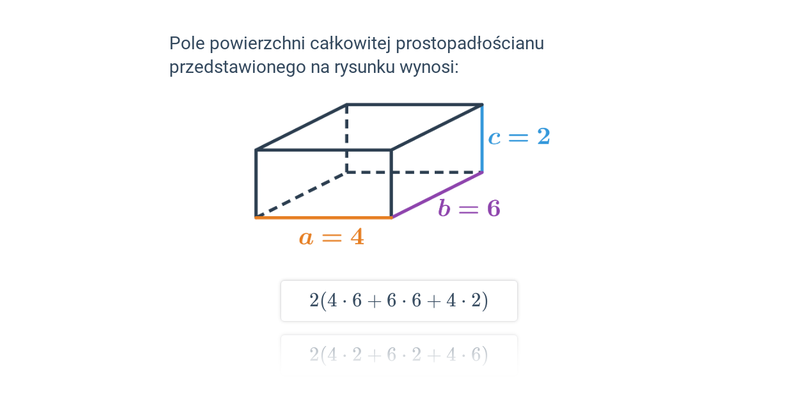
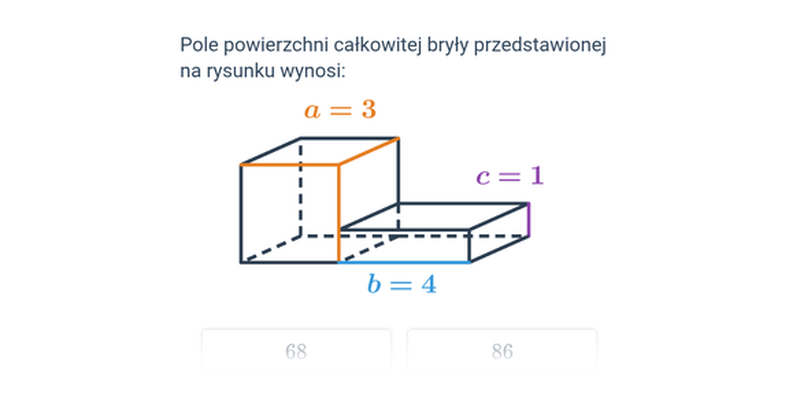
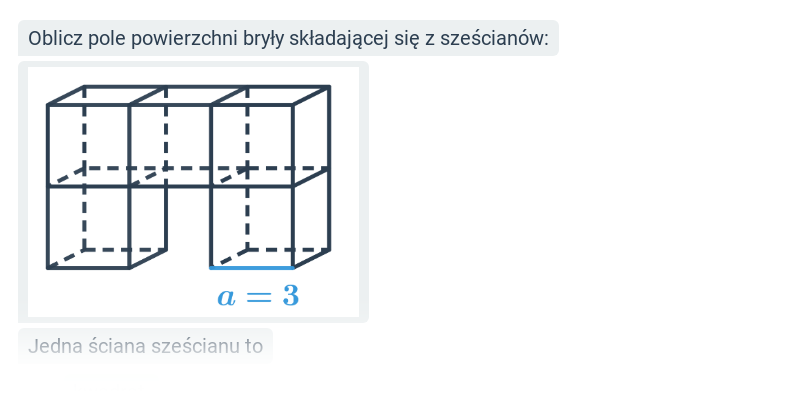
Pole powierzchni całkowitej bryły jest sumą pól wszystkich jej ścian. Możemy je sobie wyobrazić jako wielkość kolorowego papieru, który potrzebujemy do „oklejenia” bryły. Pole powierzchni całkowitej wyrażamy w jednostkach pola powierzchni.
Oznaczenia we wzorach
| V | objętość |
| P_c | pole powierzchni całkowitej |
| P_p | pole podstawy |
| P_b | pole powierzchni bocznej |
| a, b, c | długości krawędzi |
| r | promień |
| h | wysokość |
| l | tworząca stożka |
Wzory
| Bryła | Objętość | Pole powierzchni całkowitej |
|---|---|---|
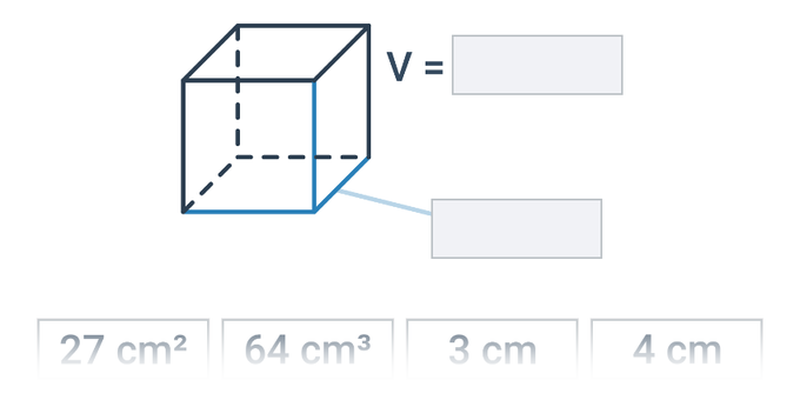
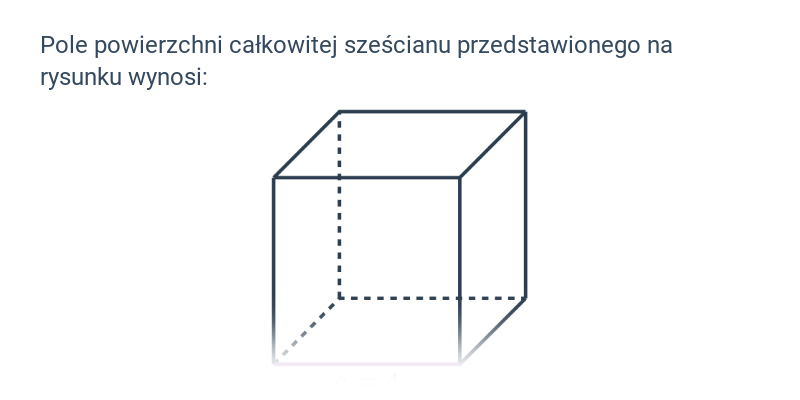
| sześcian | V = a^3 | P_c=6a^2 |
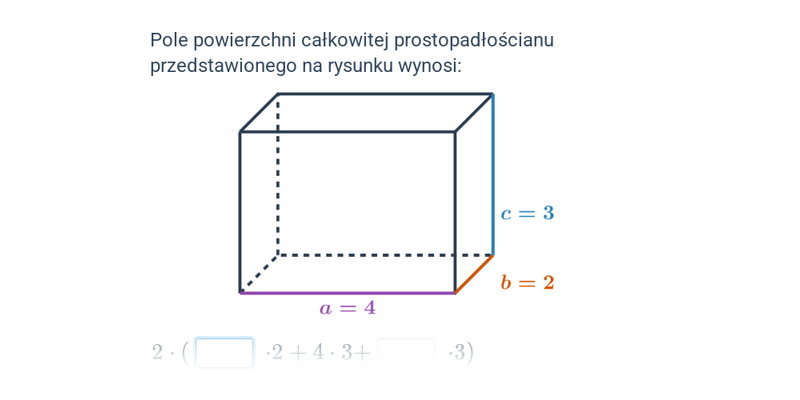
| prostopadłościan | V = abc | P_c = 2(ab+ac+bc) |
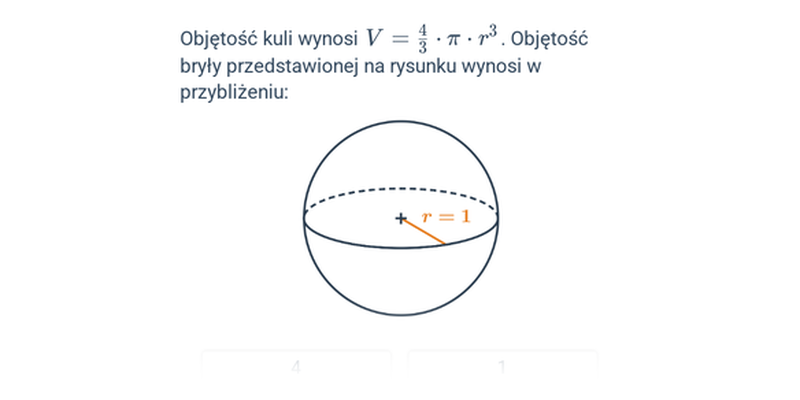
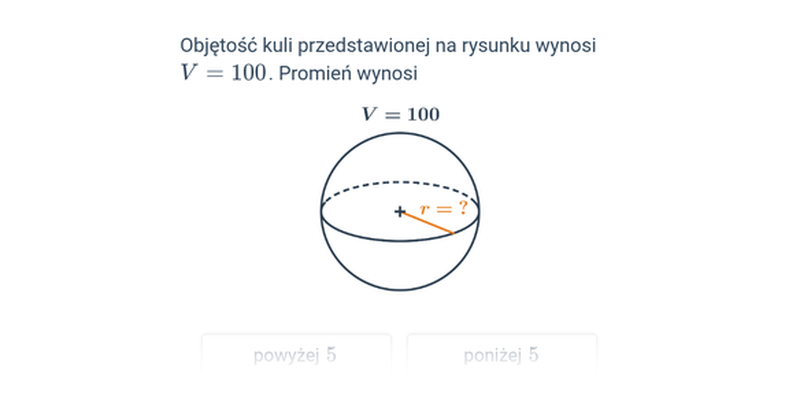
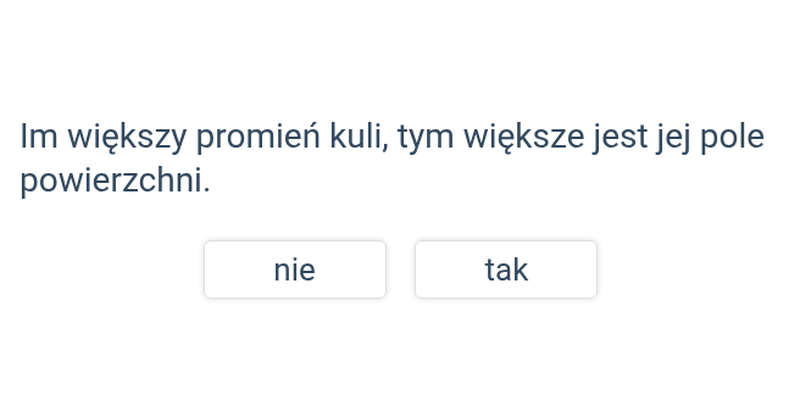
| kula | V=\frac43\pi r^3 | P=4\pi r^2 |
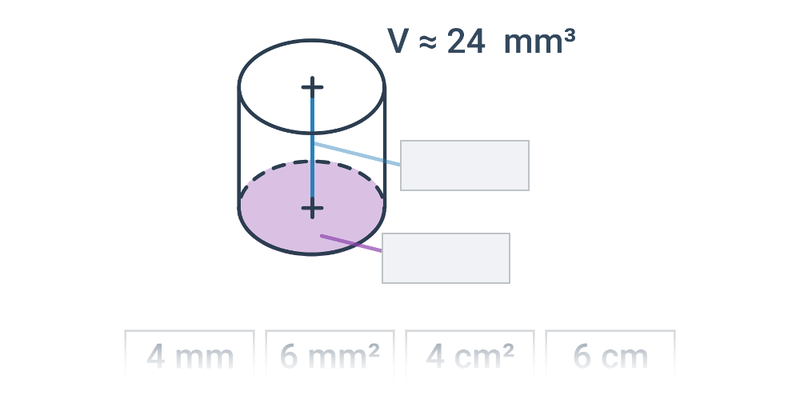
| walec | V=P_p\cdot h =\pi r^2 h | P_c=2P_p+P_b =2\pi r(r+h) |
| stożek | V=\frac{1}{3}P_p\cdot h =\frac13 \pi r^2 h | P_c =P_p+P_b =\pi r(r+\sqrt{r^2+h^2})=\pi r^2 +\pi rl |
| ostrosłup | V=\frac{1}{3}P_p\cdot h | P_c=P_p+P_b |
| ostrosłup prawidłowy czworokątny | V=\frac{1}{3}P_p\cdot h=\frac{1}{3} a^2h | |
| graniastosłup | V= P_p\cdot h | P_c=2\cdot P_p+P_b |
Przesuwanie
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.
Objętość sześcianu i prostopadłościanu (średnie) • FSL
Średni czas rozwiązywania: 7 min
Objętość brył obrotowych (średnie) • FP6
Średni czas rozwiązywania: 5 min
Decydowanie
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.
Objętość sześcianu i prostopadłościanu (średnie) • GBD
Średni czas rozwiązywania: 5 min
Objętość wielościanów (średnie) • GBG
Średni czas rozwiązywania: 5 min
Objętość walca (trudne) • GBH
Średni czas rozwiązywania: 5 min
Objętość kuli (średnie) • GC4
Średni czas rozwiązywania: 5 min
Objętość kuli (trudne) • GBC
Średni czas rozwiązywania: 5 min
Objętość brył obrotowych (średnie) • GDB
Średni czas rozwiązywania: 5 min
Objętość brył obrotowych (trudne) • GBB
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej sześcianu i prostopadłościanu (średnie) • GBW
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej sześcianu i prostopadłościanu (trudne) • GD3
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej kuli (średnie) • GEC
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej kuli (trudne) • GB4
Średni czas rozwiązywania: 5 min
Objętość, pole: wzory, zasady (średnie) • FH6
Średni czas rozwiązywania: 5 min
Objętość, pole: wzory, zasady (trudne) • FKH
Średni czas rozwiązywania: 5 min
Krok po kroku
Uzupełnianie poszczególnych kroków dłuższego zadania.
Objętość i powierzchnia: prostopadłościan, ostrosłup, graniastosłup (średnie) • FKE
Średni czas rozwiązywania: 5 min
Wpisywanie odpowiedzi
Ćwiczenie, w którym wpisujesz odpowiedź na klawiaturze.
Objętość sześcianu i prostopadłościanu (średnie) • GBM
Średni czas rozwiązywania: 5 min
Objętość sześcianu i prostopadłościanu (trudne) • GBN
Średni czas rozwiązywania: 5 min
Objętość walca (średnie) • GBU
Średni czas rozwiązywania: 5 min
Objętość stożka (średnie) • GBV
Średni czas rozwiązywania: 5 min
Objętość kuli (średnie) • GBT
Średni czas rozwiązywania: 5 min
Objętość brył obrotowych (średnie) • FJF
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej sześcianu i prostopadłościanu (łatwe) • GM9
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej sześcianu i prostopadłościanu (średnie) • GCA
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej sześcianu i prostopadłościanu (trudne) • GCB
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej walca (łatwe) • GUA
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej walca (średnie) • GCG
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej walca (trudne) • GUB
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej stożka (średnie) • GCJ
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej kuli (średnie) • GCH
Średni czas rozwiązywania: 5 min
Pole powierzchni całkowitej brył obrotowych (średnie) • FJG
Średni czas rozwiązywania: 5 min
Objętość, pole powierzchni całkowitej: miks przykładów (średnie) • FJR
Średni czas rozwiązywania: 5 min
Zadania tekstowe
Klasyczne zadania z rozmaitymi przykładami oraz komentarzami do odpowiedzi.
Objętość, pole powierzchni całkowitej: miks przykładów (średnie) • EK2
Średni czas rozwiązywania: 5 min
Objętość, pole powierzchni całkowitej: miks przykładów (trudne) • E27
Średni czas rozwiązywania: 5 min
Objętość i pole powierzchni całkowitej: prostopadłościan, ostrosłup, graniastosłup (średnie) • FKF
Średni czas rozwiązywania: 5 min
Objętość i pole powierzchni całkowitej: prostopadłościan, ostrosłup, graniastosłup (trudne) • FKN
Średni czas rozwiązywania: 5 min
Objętość i pole powierzchni całkowitej: kula, walec, stożek (średnie) • FKJ
Średni czas rozwiązywania: 5 min
Objętość i pole powierzchni całkowitej: kula, walec, stożek (trudne) • FKO
Średni czas rozwiązywania: 5 min
