Dziękujemy za ocenę.

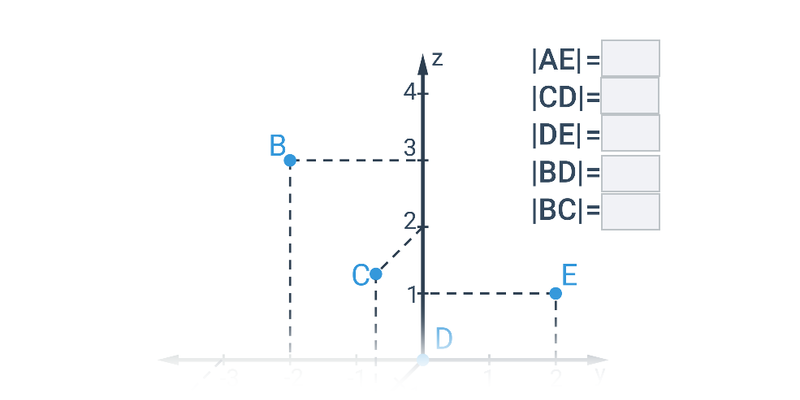
Odległość między punktami w przestrzeni

Odległość między dwoma punktami w przestrzeni obliczamy podobnie jak odległość między dwoma punktami na płaszczyźnie, czyli za pomocą współrzędnych. Jeżeli dane są współrzędne punktów A=[a_x,a_y,a_z], B=[b_x,b_y,b_z], odległość między tymi punktami możemy obliczyć w następujący sposób:

|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2 + (b_z-a_z)^2}

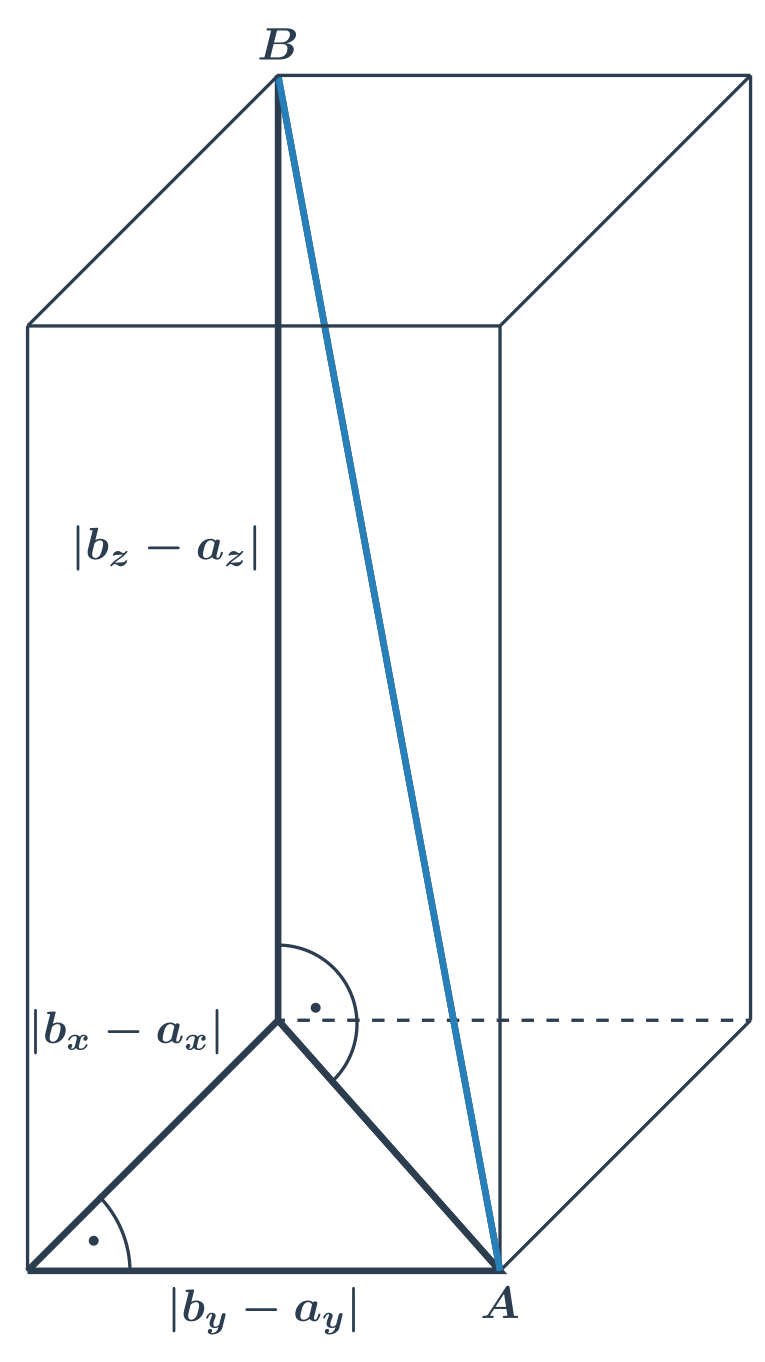
W podobny sposób (stosując dwa razy z rzędu twierdzenie Pitagorasa) możemy obliczyć długość przekątnej prostopadłościanu.

Przykład: odległość C[1;2;0],D[4;5;1]

|CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2 + (d_z-c_z)^2}
Podstawiamy współrzędne punktów C[1;2;0] i D[4;5;1]: \sqrt{(4-1)^2 + (5-2)^2 + (1-0)^2}=\sqrt{3^2 + 3^2 + 1^2}=\sqrt{19}
Odległość wynosi: |CD|=\sqrt{19}

Przykład: odległość M[0;-1;3], N[-4;1;-1]

|MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2 + (n_y-m_y)^2}
Podstawiamy współrzędne punktów M[0;-1;3] i N[-4;1;-1]: \sqrt{(-4-0)^2 + (1-(-1))^2 + (-1-3)^2}=\sqrt{(-4)^2 + 2^2+(-4)^2}=\sqrt{36}=6
Odległość wynosi: |MN|=6