Porównywanie ułamków dziesiętnych
Porównując ułamki dziesiętne, musimy znaleźć „najważniejszy“ element, którym różnią się od siebie, a następnie wykonać porównanie na jego podstawie. Czyli najpierw porównujemy części całkowite. Jeżeli części całkowite są takie same, przechodzimy do porównywania kolejnych cyfr, czyli części dziesiątych, setnych, tysięcznych itd. Nie zapomnijmy skontrolować znaku, który ma takie same znaczenie jak w przypadku liczb całkowitych. Przykłady:
15{,}3 < 17{,}9987 – ułamki różnią się częścią całkowitą, czyli na potrzeby porównania możemy całkowicie zignorować części ułamkowe.
0{,}2 > 0{,}17 – części całkowite są takie same, zatem bierzemy pod uwagę części dziesiąte, gdzie 2>1. W przykładach tego typu często popełniany jest błąd, który wynika z tego, że na pierwszy rzut oka wydaje się, że 17 > 2. Dla ułatwienia warto rozszerzyć część ułamkową, czyli dodać zero z prawej strony: 0{,}20 > 0{,}17.
3{,}21 > -3{,}22 – tu w ogóle nie mają znaczenia części ułamkowe, ponieważ pierwsza liczba jest dodatnia, a druga ujemna.
-4{,}2791 < -4{,}2758 – porównujemy na podstawie cyfr w miejscu części tysięcznych (9 i 5), wynik jest „odwrotny“, ponieważ są to liczby ujemne.
Przesuwanie
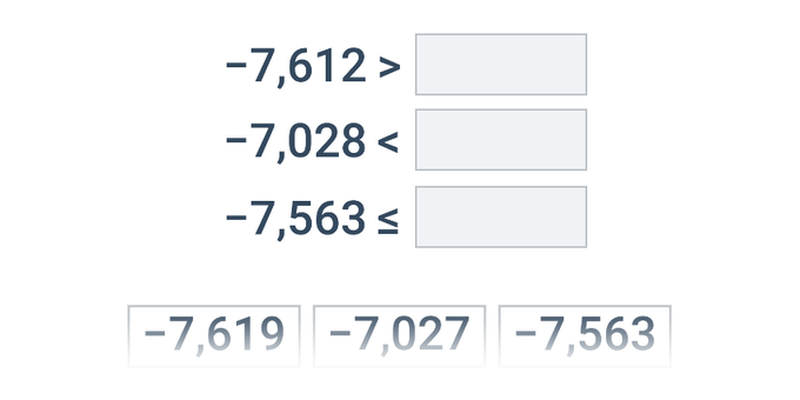
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.
Decydowanie
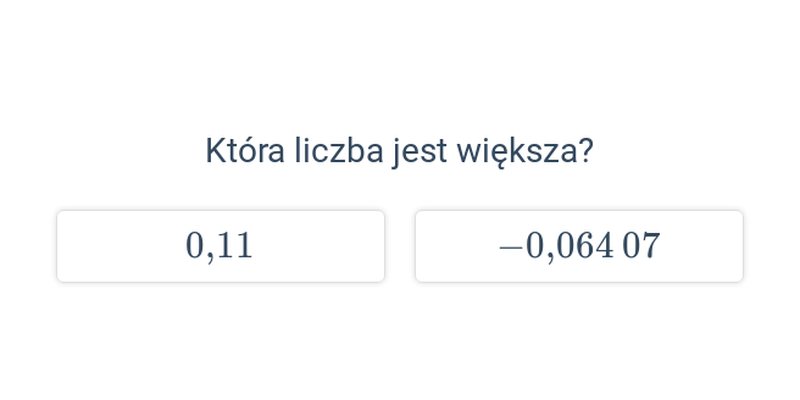
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.