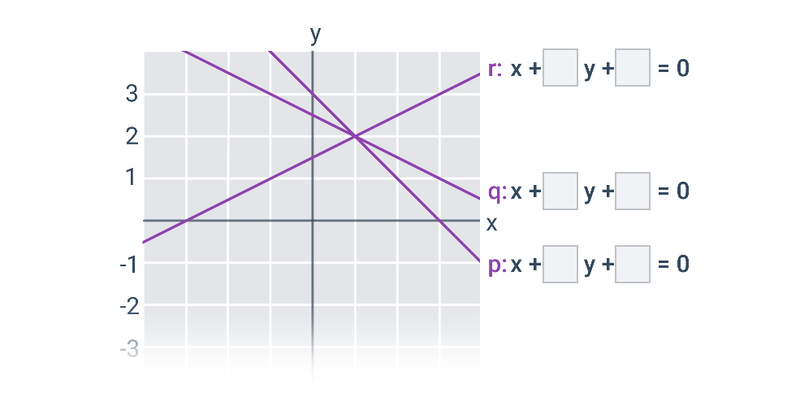
Równanie ogólne prostej w ukł. współrzędnych

Równanie ogólne prostej na płaszczyźnie ma postać: ax+by+c=0, gdzie a i b to współrzędne wektora normalnego, a c to liczba rzeczywista. Wektor normalny \vec{n}=(a;b) jest prostopadły do danej prostej, a więc również prostopadły do jej wektora kierunkowego.

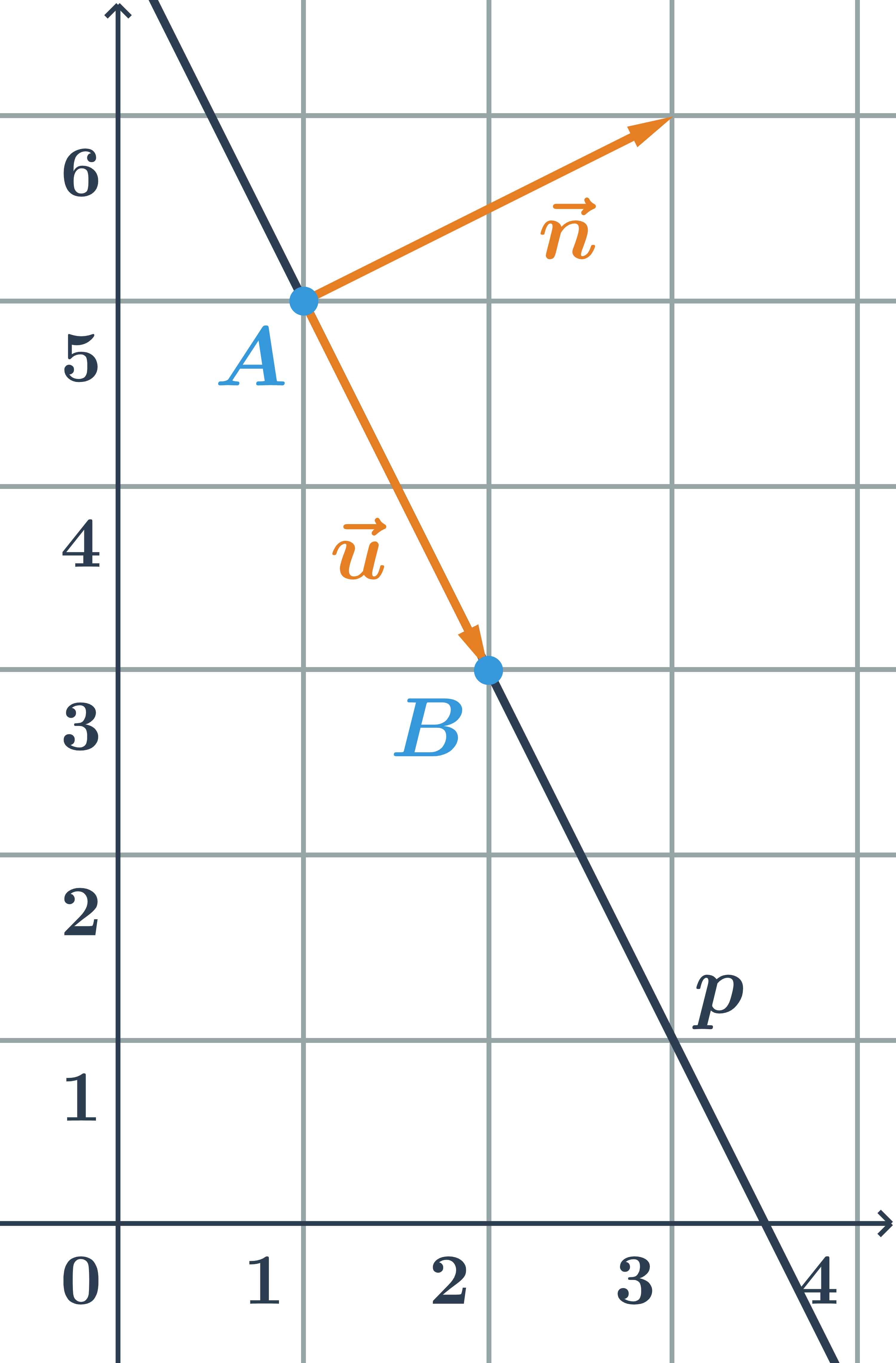
Równanie ogólne prostej p wyznaczonej przez punkty A=[1;5] i B=[2;3]

Prosta p jest wyznaczona przez punkt A oraz wektor kierunkowy \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
Wektor normalny jest prostopadły do wektora \vec{u}=(1;-2), zatem może to być na przykład wektor \vec{n}=(2;1).
Współrzędne wektora normalnego to a i b w równaniu ogólnym prostej. Równanie ogólne ma postać: 2x+y+c=0
Aby obliczyć c, podstawiamy współrzędne punktu A=[1;5] :
2\cdot1+5+c=0\Rightarrow c=-7
Zatem równanie ogólne prostej p to: 2x+y-7=0

Ogólne równanie prostej danej parametrycznie

Wyznacz równanie ogólne prostej p, która jest dana następującym parametrycznym układem równań: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}

Prosta p jest wyznaczona przez punkt A=[1;4] oraz wektor kierunkowy \vec{u}=(2;6).
Współrzędne wektora kierunkowego można uprościć do postaci: \vec{u}=(1;3).
Wektor normalny jest prostopadły do wektora \vec{u}=(1;3), zatem może to być na przykład wektor \vec{n}=(3;-1).
Współrzędne wektora normalnego to a i b w równaniu ogólnym prostej. Równanie ogólne ma postać: 3x-y+c=0
Aby obliczyć c, podstawiamy współrzędne punktu A=[1;4] :
3\cdot1-4+c=0\Rightarrow c=1
Zatem równanie ogólne prostej p to: 3x-y+1=0

Parametryczne wyrażenie prostej danej równaniem ogólnym

Wyznacz parametryczne równanie prostej p, której równanie ogólne to: 3x-2y+4=0.

Prosta p ma wektor normalny \vec{n}=(3;-2).
Wektor kierunkowy jest prostopadły do wektora \vec{n}=(3;-2), czyli może to być na przykład wektor \vec{u}=(2;3).
Wyznaczamy jeden punkt na prostej p : jedną współrzędną możemy wybrać dowolnie, np. x=0, drugą obliczamy: 3\cdot0-2y+4=0\Rightarrow y=2
Z równania ogólnego wynika więc, że na prostej leży punkt A=[0;2].
Zatem równanie parametryczne prostej p to: \begin{array}{rrl}x&=&0+2t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}