Język polski
Język angielski
Informatyka
Język niemiecki
Umiemy to
Działania na liczbach
Ułamki zwykłe, procenty, ułamki dziesiętne
Geometria
Wyrażenia algebraicze, równania, nierówności
Funkcje
Jednostki miary
Kombinatoryka, zbiory, logika
Wiedza finansowa
Decydowanie
Krok po kroku
Wykresownik
Zaznaczanie
Przesuwanie
Kratki
Rozdzielanie
Zepsuty kalkulator
Roboty
Potworki
Wyścigi
Terytoria
Drużynówka
Moje konto
Wyloguj sięRozwiąż też
Ćwiczenia
Symbol Newtona
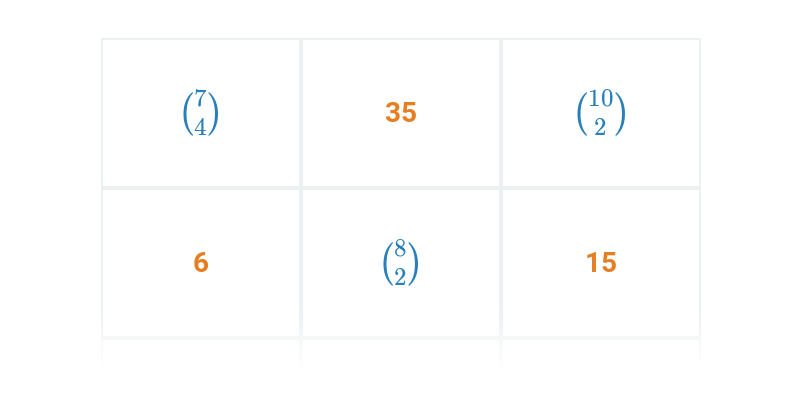
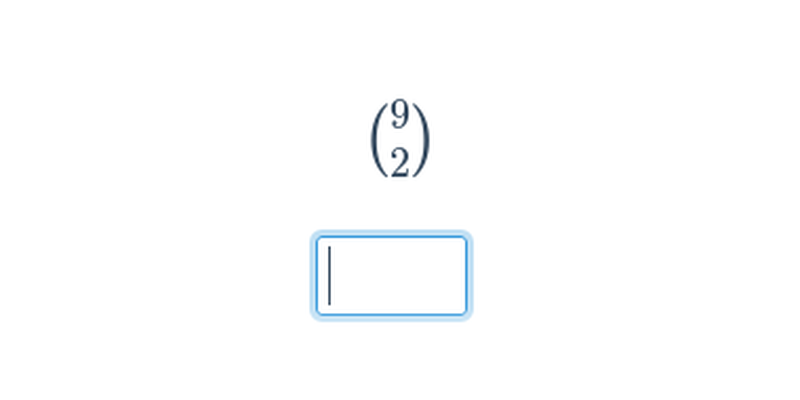
Symbol Newtona określa liczbę kombinacji, czyli sposobów, na które możemy wybrać k elementów ze zbioru n-elementowego. Z symbolem Newtona spotykamy się w kombinatoryce. Oznaczamy go jako \binom{n}{k} (odczytujemy „n nad k“).
Dla n \geq k \geq 0 symbol Newtona przyjmuje postać: \binom{n}{k} = \frac{n!}{k!(n-k)!}
Dla symbolu Newtona zachodzą również inne zależności, na przykład:
- \binom{n}{k} = \binom{n}{n-k}
- \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}
- \sum_{k=0}^n \binom{n}{k} = 2^n
Przykłady:
| \binom{3}{1} | = 2 |
| \binom{4}{2} | = 6 |
| \binom{5}{3} | = 10 |
| \binom{6}{2} | = 15 |
| \binom{15}{15} | = 1 |
Wyjaśnienie mi pomogło
Wyjaśnienie mi nie pomogło
Memory
Szukanie pasujących par.
Symbol Newtona 
Pokaż wyjaśnienie do tematu
trudne
Symbol Newtona (trudne)
Zadania: 5
Średni czas rozwiązywania: 5 min
Wpisywanie odpowiedzi
Ćwiczenie, w którym wpisujesz odpowiedź na klawiaturze.
Symbol Newtona
Pokaż wyjaśnienie do tematu
średnie
Symbol Newtona (średnie)
Zadania: 31
Średni czas rozwiązywania: 5 min
