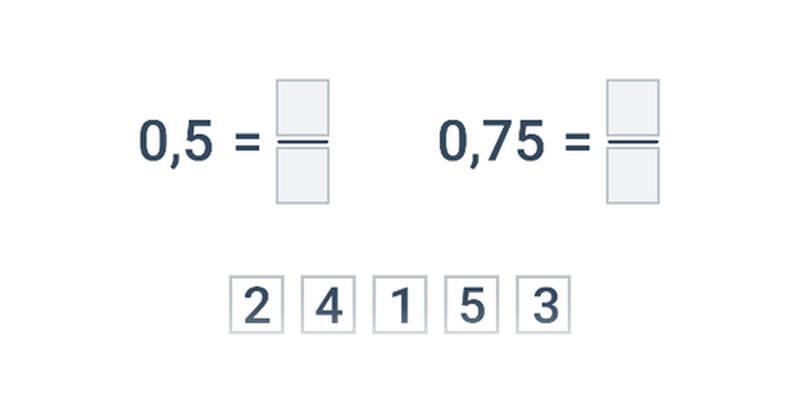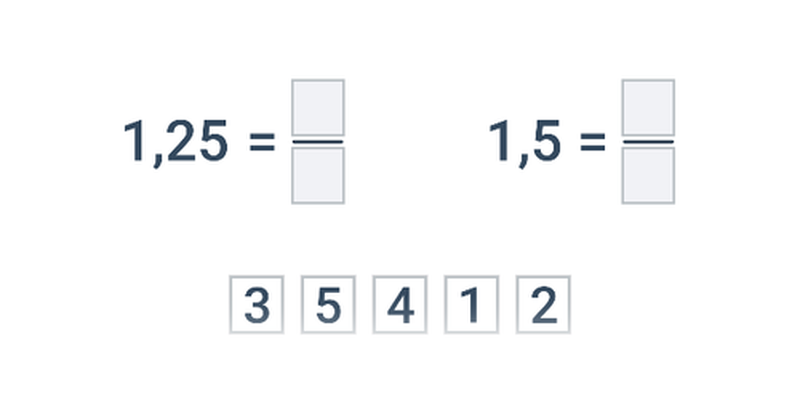Ułamki zwykłe i dziesiętne
Zamiana ułamka dziesiętnego na zwykły
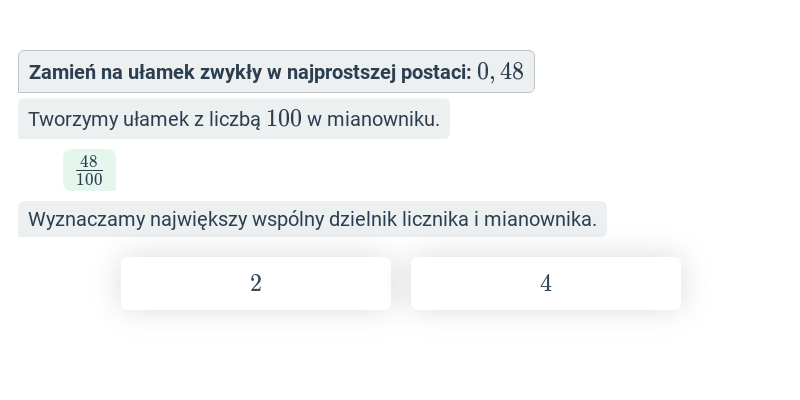
Ułamek dziesiętny mnożymy przez 10, 100, 1000 (lub inną odpowiednią potęgę liczby 10), aby „pozbyć się” przecinka. Następnie przy pomocy największego wspólnego dzielnika sprowadzamy otrzymany ułamek do najprostszej postaci.
1{,}5 = 1{,}5\cdot \frac{10}{10} = \frac{1{,}5\cdot 10}{10} = \frac{15}{10} = \frac{3}{2}
1{,}25 = 1{,}25 \cdot \frac{100}{100} = \frac{1{,}25\cdot 100}{100} = \frac{125}{100} = \frac{5}{4}
Warto zapamiętać kilka najczęstszych przykładów, dzięki którym szybciej rozwiążemy inne, bardziej skomplikowane zadania.
0{,}01 = \frac{1}{100}
0{,}1 = \frac{1}{10}
0{,}2 = \frac{1}{5}
0{,}25 = \frac{1}{4}
0{,}333\ldots = \frac{1}{3}
0{,}5 = \frac{1}{2}
Zamiana ułamka zwykłego na dziesiętny
Wartość ułamka zwykłego to iloraz licznika i mianownika. Zatem aby zamienić ułamek zwykły na dziesiętny, wystarczy podzielić licznik przez mianownik (można zastosować metodę dzielenia „pod kreską”).
Przykłady:
\frac{3}{4} = 3:4 = 0{,}75
\frac{6}{5} = 6:5 = 1{,}2
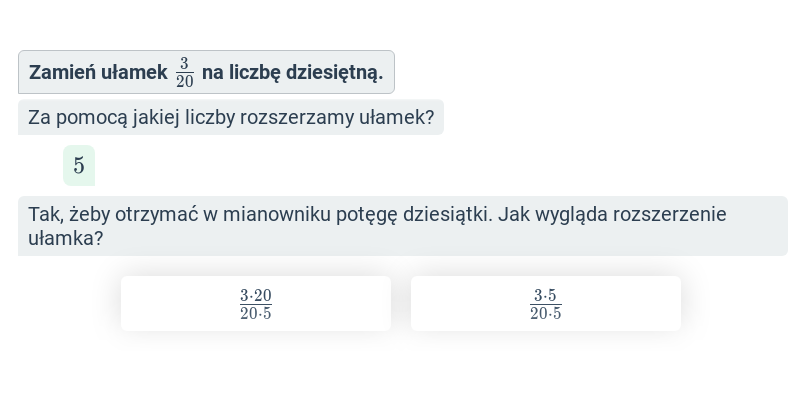
\frac{3}{20} = 3:20 = 0{,}15
Przesuwanie
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.
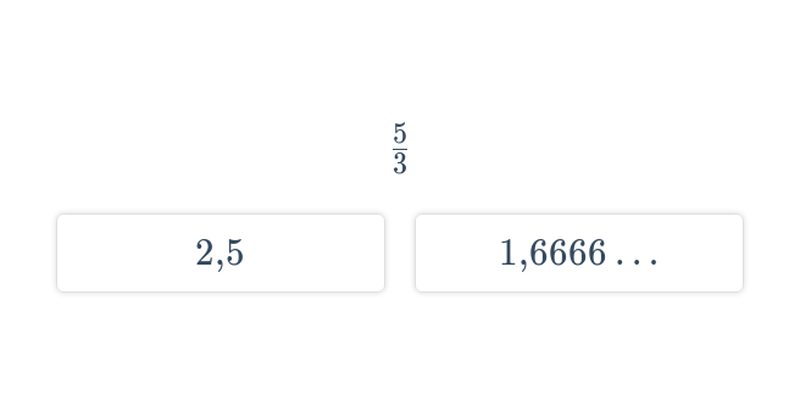
Decydowanie
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.
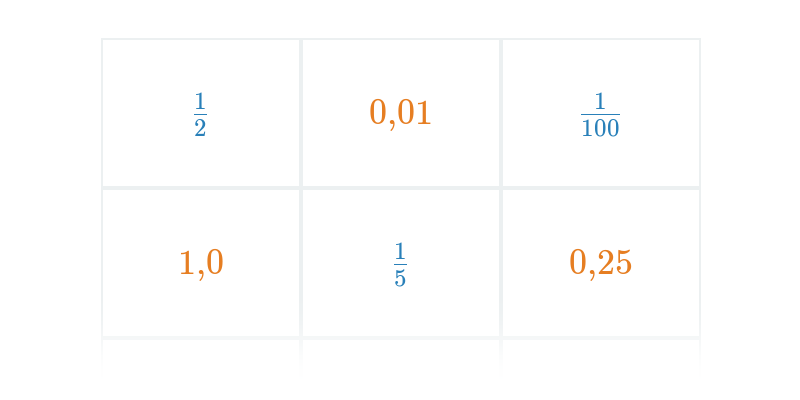
Krok po kroku
Uzupełnianie poszczególnych kroków dłuższego zadania.