Zbiory: pojęcia

Zbiór to zestaw elementów. W zbiorze nie ma znaczenia kolejność elementów ani to, czy się powtarzają. Poniższe zbiory są zatem takie same:

Symbol	Znaczenie	Komentarz
\emptyset	zbiór pusty
\overline{A}	dopełnienie	elementy, które nie należą do zbioru A
x \in A	należy do zbioru	elementy x należą do zbioru A
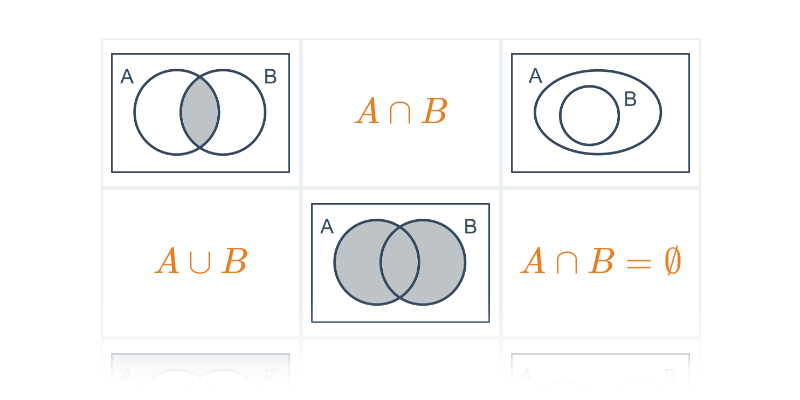
A \cap B	część wspólna	elementy, które należą do obu zbiorów A, B
A \cup B	suma zbiorów	elementy, które należą do któregokolwiek ze zbiorów A, B
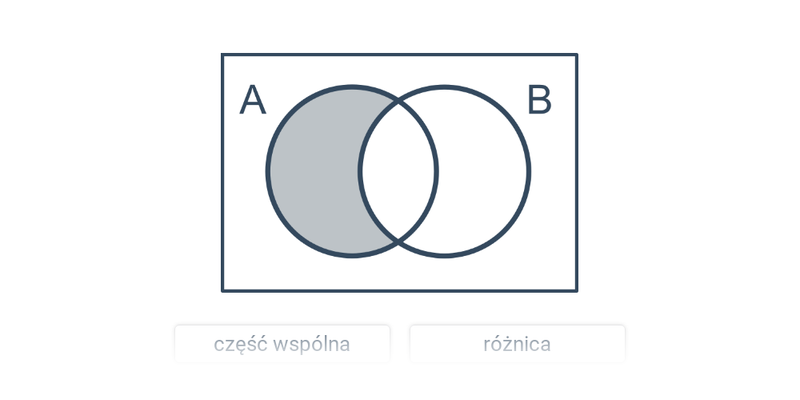
A \setminus B	różnica	elementy, które należą do zbioru A, ale nie należą do zbioru B
A = B	równość	równość zbiorów A, B
A \subseteq B	podzbiór	wszystkie elementy zbioru A należą również do zbioru B
A \subset B	podzbiór właściwy	A jest podzbiorem B i jednocześnie A \neq B
$	A	$
A \cap B = \emptyset	zbiory rozłączne	zbiory A, B nie mają żadnego elementu wspólnego