Język polski
Język angielski
Informatyka
Język niemiecki
Umiemy to
Działania na liczbach
Ułamki zwykłe, procenty, ułamki dziesiętne
Geometria
Wyrażenia algebraicze, równania, nierówności
Funkcje
Jednostki miary
Kombinatoryka, zbiory, logika
Wiedza finansowa
Decydowanie
Memory
Krok po kroku
Wpisywanie odpowiedzi
Wykresownik
Zaznaczanie
Przesuwanie
Kratki
Rozdzielanie
Zepsuty kalkulator
Roboty
Potworki
Wyścigi
Terytoria
Drużynówka
Moje konto
Wyloguj się
Krok po kroku
Środek odcinka w ukł. współrzędnych
Dostęp bez ograniczeńKorzystasz z platformy z limitem dziennym na liczbę odpowiedzi. Aby zwiększyć limit lub uzyskać dostęp do konta z licencją, zaloguj się.
Zaloguj się
GNAkod QR
Kod / krótki adres
Skopiuj kliknięciem.
Środek odcinka w ukł. współrzędnych
Środek odcinka dzieli odcinek na dwie równe części. Jeżeli końce odcinka AB leżą na osi liczbowej, a ich położeniu odpowiadają wartości a i b, to środku odcinka S odpowiada liczba s=\frac{a+b}{2}. Środek odcinka jest więc „średnią arytmetyczną“ jego końców.
Dla odcinka w układzie współrzędnych sytuacja wygląda następująco: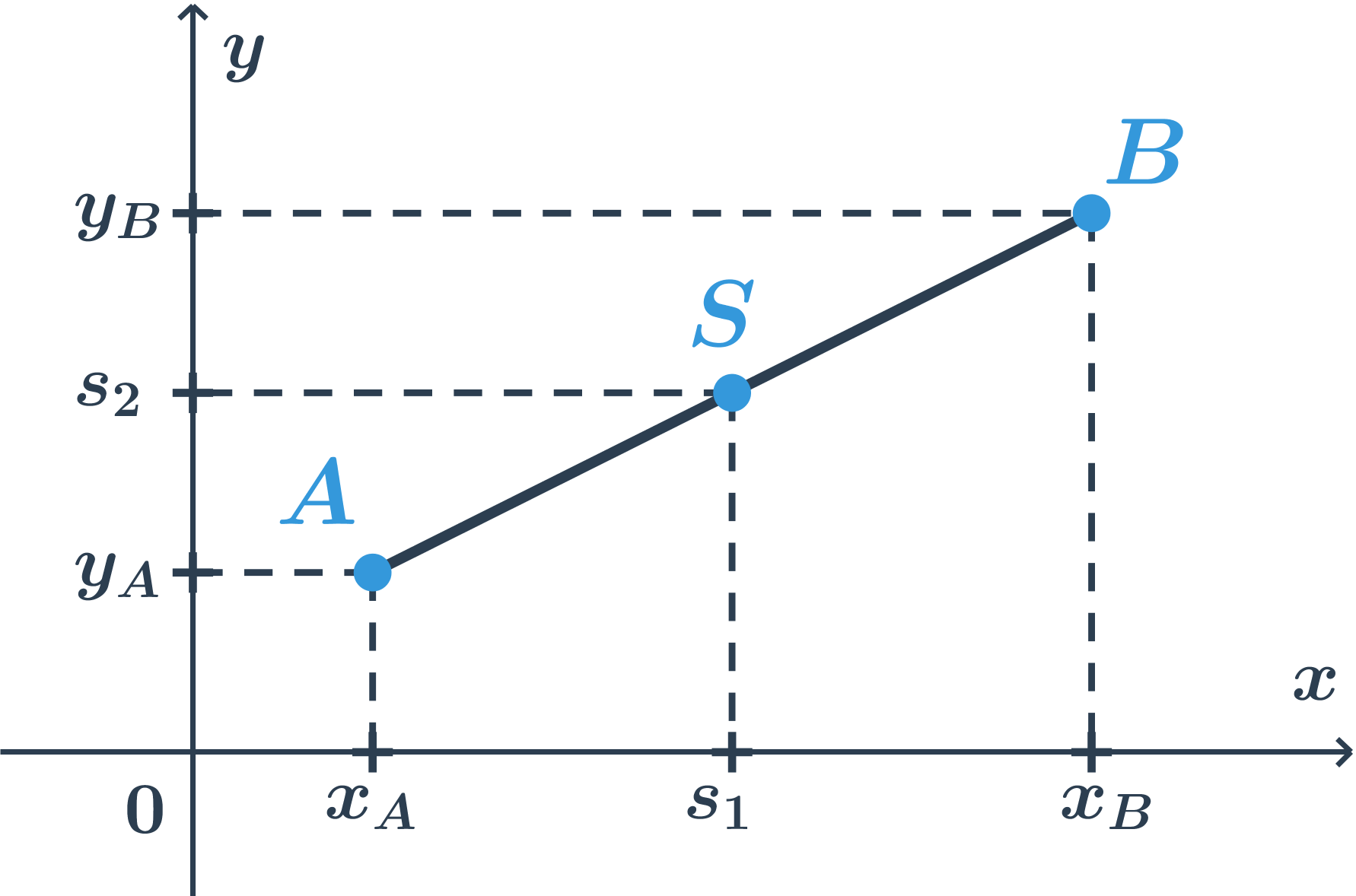 
Mamy tu dwie osie. I znów, aby wyznaczyć współrzędne środka odcinka, musimy obliczyć średnie arytmetyczne poszczególnych współrzędnych końców odcinka.
Zatem środek S[s_1;s_2] odcinka AB, gdzie A[x_A; y_A], B[x_B; y_B] ma współrzędne:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Przykład: wyznacz środek odcinka
Znajdź środek odcinka AB: A[6;-1], B[2;3]
- Współrzędne środka S[s_1;s_2]: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Podstawiamy współrzędne punktów A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Środkiem odcinka AB jest punkt S[4;1]
Przykład: wyznacz drugi koniec odcinka
Wyznacz współrzędne drugiego końca odcinka AB, jeżeli dany jest punkt A[-3;0] oraz środek odcinka S[1;3].
- Współrzędne środka S[s_1;s_2]: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Podstawiamy współrzędne punktów A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Obliczamy niewiadome x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Punkt B ma współrzędne [5;6].
Środek odcinka w ukł. współrzędnych (łatwe)
Rozwiązane:
