Symetria osiowa jest określona przez prostą o i przyporządkowuje każdemu punktowi X spoza osi taki punkt X', że prosta o jest osią odcinka XX'. Innymi słowy, obraz ma taką samą odległość od osi jak punkt pierwotny, a odcinek łączący te dwa punkty jest prostopadły do osi. Symetria osiowa zachowuje odległości i kąty, więc jest przekształceniem przystającym.

Przykłady

Niebieskie i pomarańczowe figury są symetryczne względem osi o:

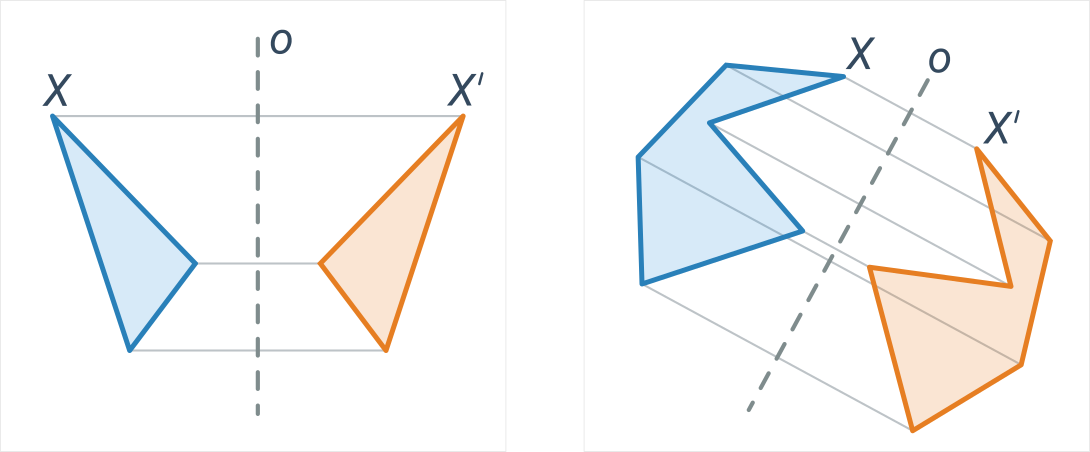
Dla lepszego zrozumienia warto porównać symetrię osiową i środkową.

Figura osiowo symetryczna

Figurę nazywamy osiowo symetryczną, jeśli w pewnej symetrii osiowej jest obrazem samej siebie. Prostą, względem której występuje taka symetria, nazywamy osią figury. Poniższa ilustracja przedstawia przykłady figur osiowo symetrycznych (zielone, z zaznaczonymi osiami symetrii) oraz figur niesymetrycznych (czerwone):

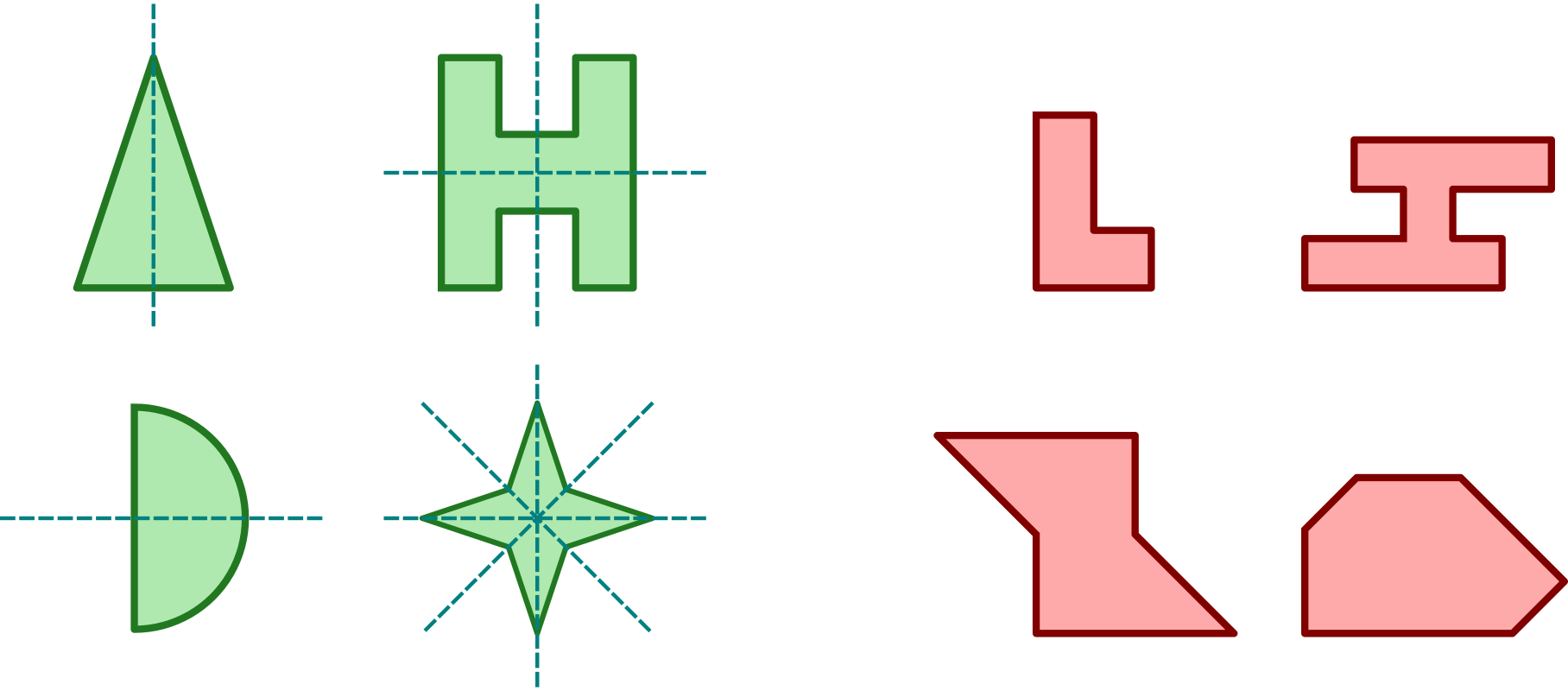
Inne przykłady:

• Odcinek jest osiowo symetryczny i ma jedną oś symetrii w płaszczyźnie (prostą prostopadłą w jego środku).
• Trójkąt równoramienny jest osiowo symetryczny.
• Trójkąt, który nie jest równoramienny, nie jest osiowo symetryczny.
• Wszystkie wielokąty foremne są osiowo symetryczne. Liczba osi symetrii jest równa liczbie wierzchołków.
• Koło jest osiowo symetryczne i ma nieskończenie wiele osi symetrii.