
Symetria środkowa

Symetria środkowa jest symetrią względem punktu S. Każdemu punktowi X przyporządkowuje taki punkt X', że punkt S jest środkiem odcinka XX'. Innymi słowy: obraz ma taką samą odległość od środka symetrii jak punkt pierwotny i leży na półprostej przeciwnej do SX.
Symetria środkowa zachowuje odległości i kąty, jest więc rodzajem przystawania. Symetria środkowa o środku w punkcie S jest równoważna obrotowi o 180 stopni względem środka symetrii S.
Przykłady
Niebieskie i pomarańczowe figury są środkowosymetryczne względem punktu S:
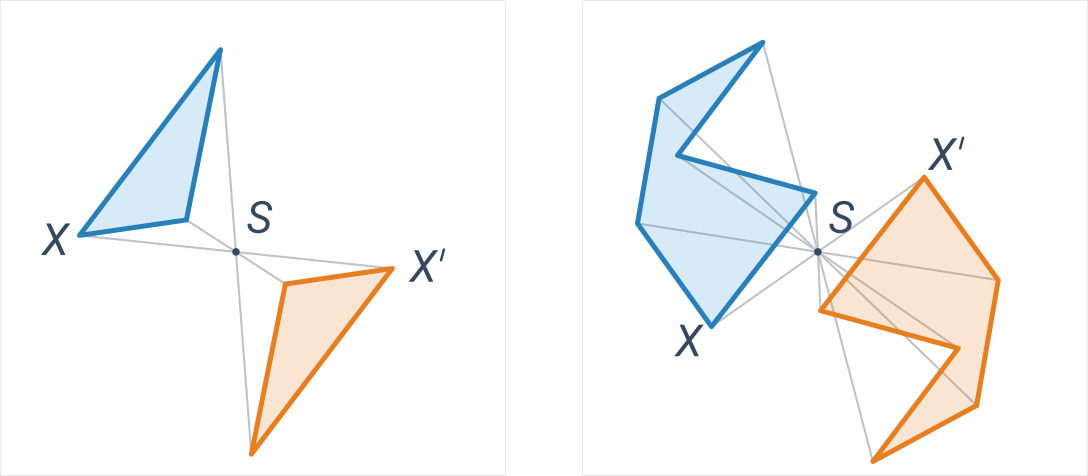
W lepszym zrozumieniu pomoże nam porównanie symetrii środkowej i osiowej.
Figura środkowosymetryczna
Figurę nazywamy środkowosymetryczną, jeśli w pewnej symetrii środkowej jest ona obrazem samej siebie. Środek tej symetrii środkowej nazywamy środkiem symetrii obiektu. Poniższy rysunek przedstawia przykłady figur środkowosymetrycznych (zielone, z zaznaczonym środkiem symetrii) oraz figur niesymetrycznych (czerwone).
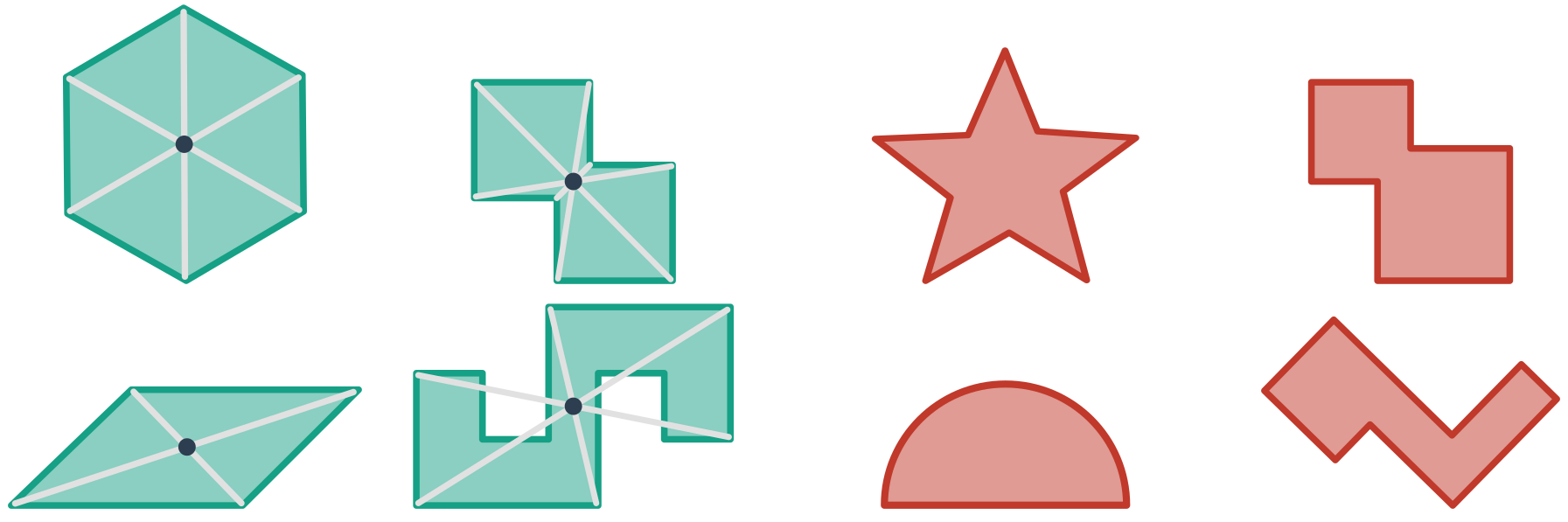
Inne przykłady:
Odcinek, prostokąt, kwadrat, romb, sześciokąt foremny oraz okrąg są środkowosymetryczne.
Żaden trójkąt nie jest środkowosymetryczny.
Zamknij













