Język polski
Język angielski
Informatyka
Język niemiecki
Umiemy to
Działania na liczbach
Ułamki zwykłe, procenty, ułamki dziesiętne
Geometria
Wyrażenia algebraicze, równania, nierówności
Funkcje
Jednostki miary
Kombinatoryka, zbiory, logika
Wiedza finansowa
Decydowanie
Memory
Krok po kroku
Wpisywanie odpowiedzi
Wykresownik
Zaznaczanie
Przesuwanie
Kratki
Rozdzielanie
Zepsuty kalkulator
Roboty
Potworki
Wyścigi
Terytoria
Drużynówka
Moje konto
Wyloguj sięKąty i okrąg – klasa 5
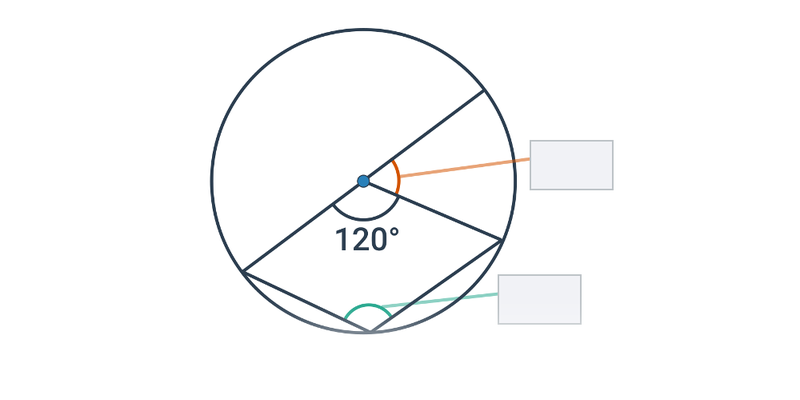
Kąt środkowy
- Kąt, którego wierzchołek leży w środku S okręgu i którego ramiona przecinają okrąg w punktach A, B. Mówimy, że kąt środkowy jest oparty na łuku AB.
- Dla dwóch dowolnych punktów na okręgu można wyznaczyć dwa kąty środkowe. Dzieje się tak dlatego, że dwa dowolne punkty dzielą okrąg na dwa łuki.
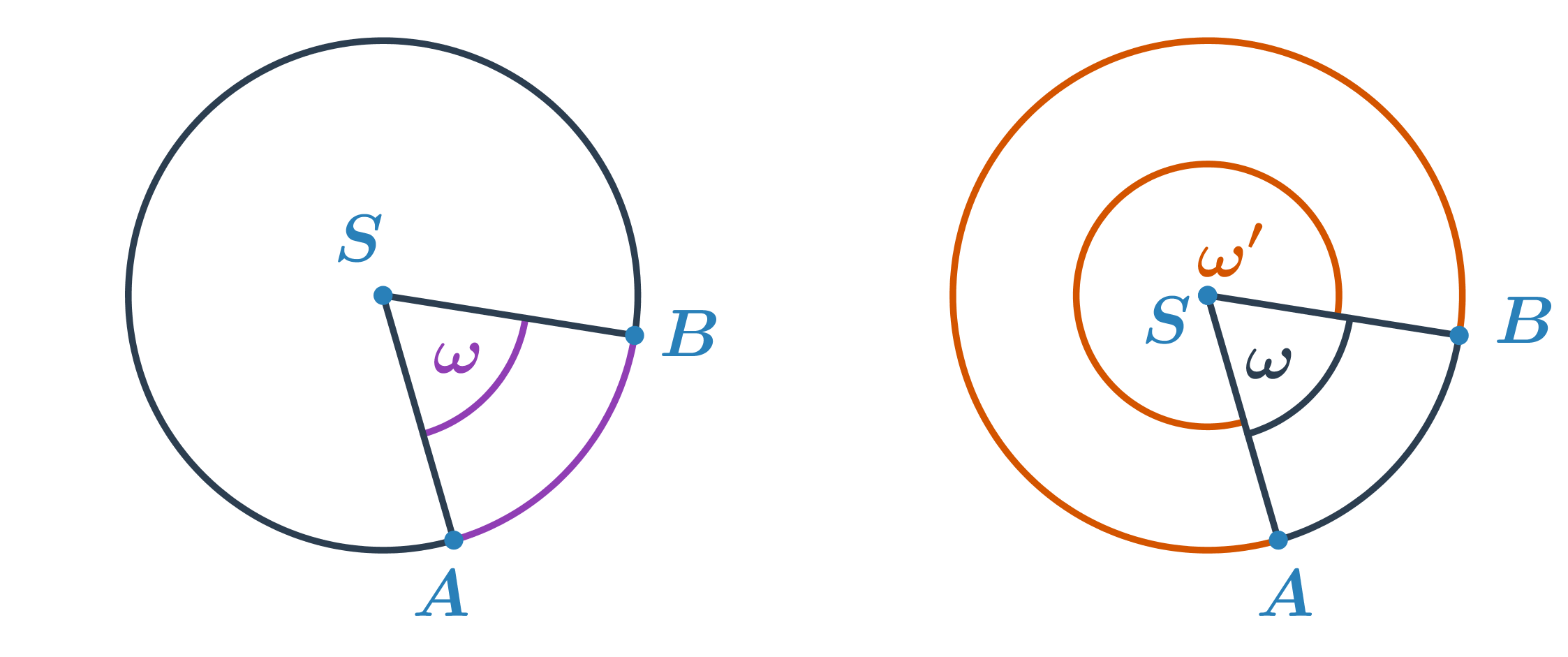
Kąt wpisany w okrąg
- Kąt, którego wierzchołek V leży na okręgu i którego ramiona przecinają okrąg w punktach A, B (A \neq V \neq B).
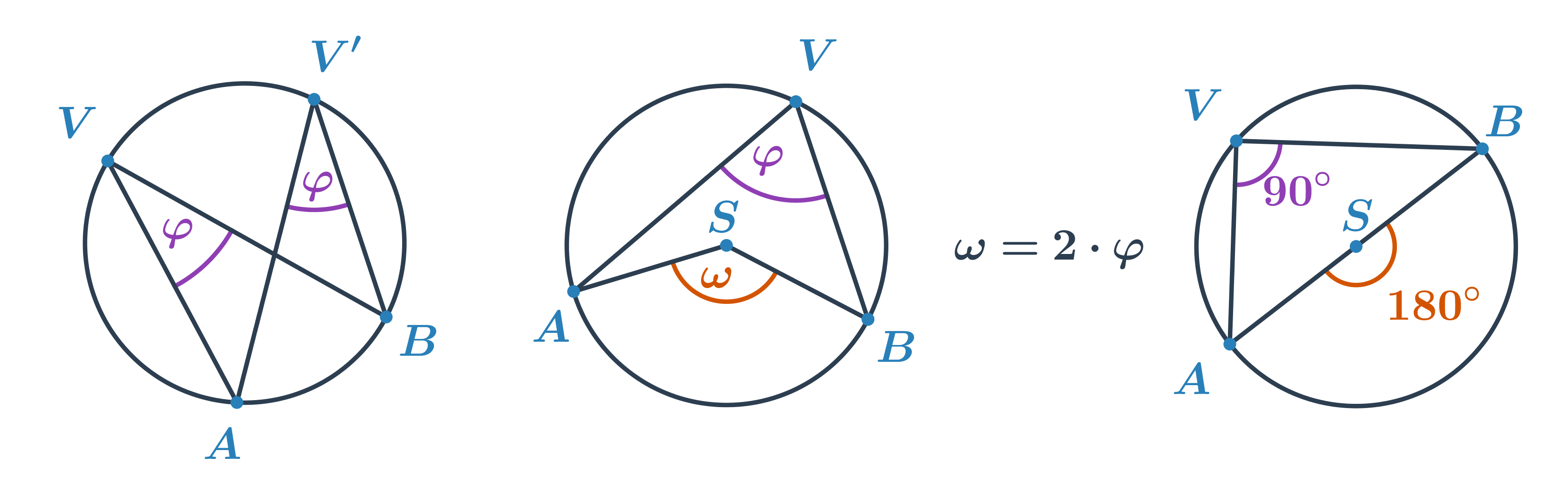
- Wszystkie kąty wpisane, które obejmują łuk AB i których wierzchołek V nie leży na łuku, mają taką samą miarę.
- Miara kąta środkowego \omega jest dwa razy większa od miary kąta wpisanego \varphi obejmującego ten sam łuk, \omega = 2\cdot\varphi.
- Twierdzenia Talesa: Kąt wpisany nad średnicą okręgu jest kątem prostym.
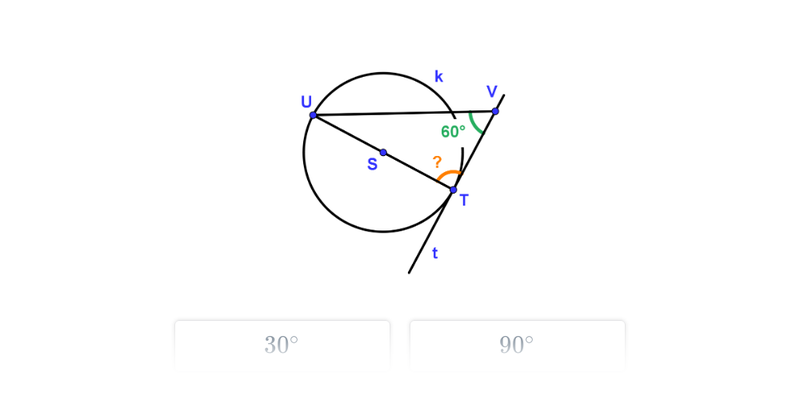
Kąt dopisany do okręgu
- Kąt między cięciwą AB okręgu i styczną t do tego okręgu w punkcie A lub B.
- Miara kąta dopisanego jest równa mierze kąta wpisanego nad łukiem AB.
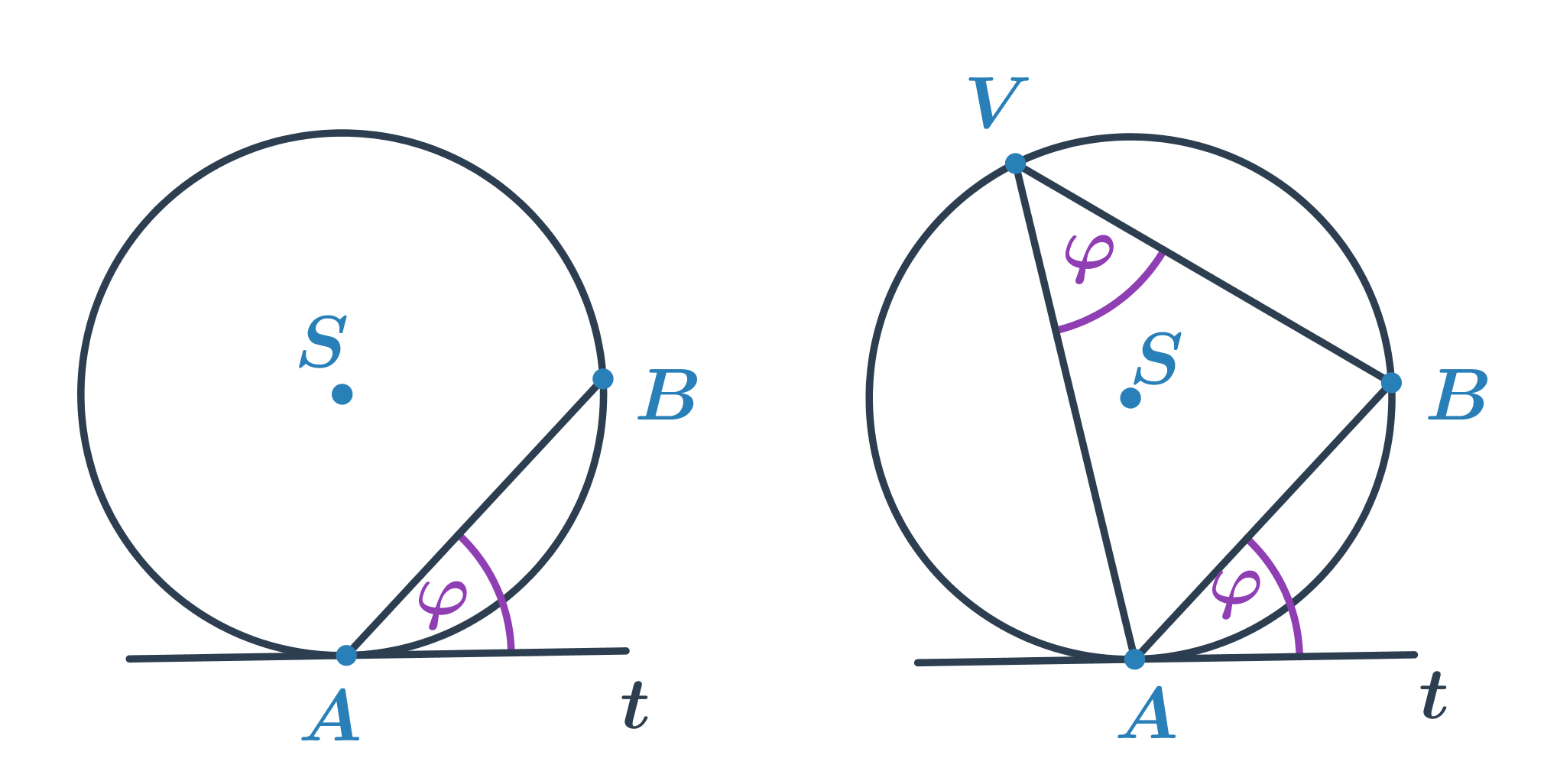
Przykład 1: Oblicz miarę kąta
Oblicz miarę kąta zaznaczonego na pomarańczowo.
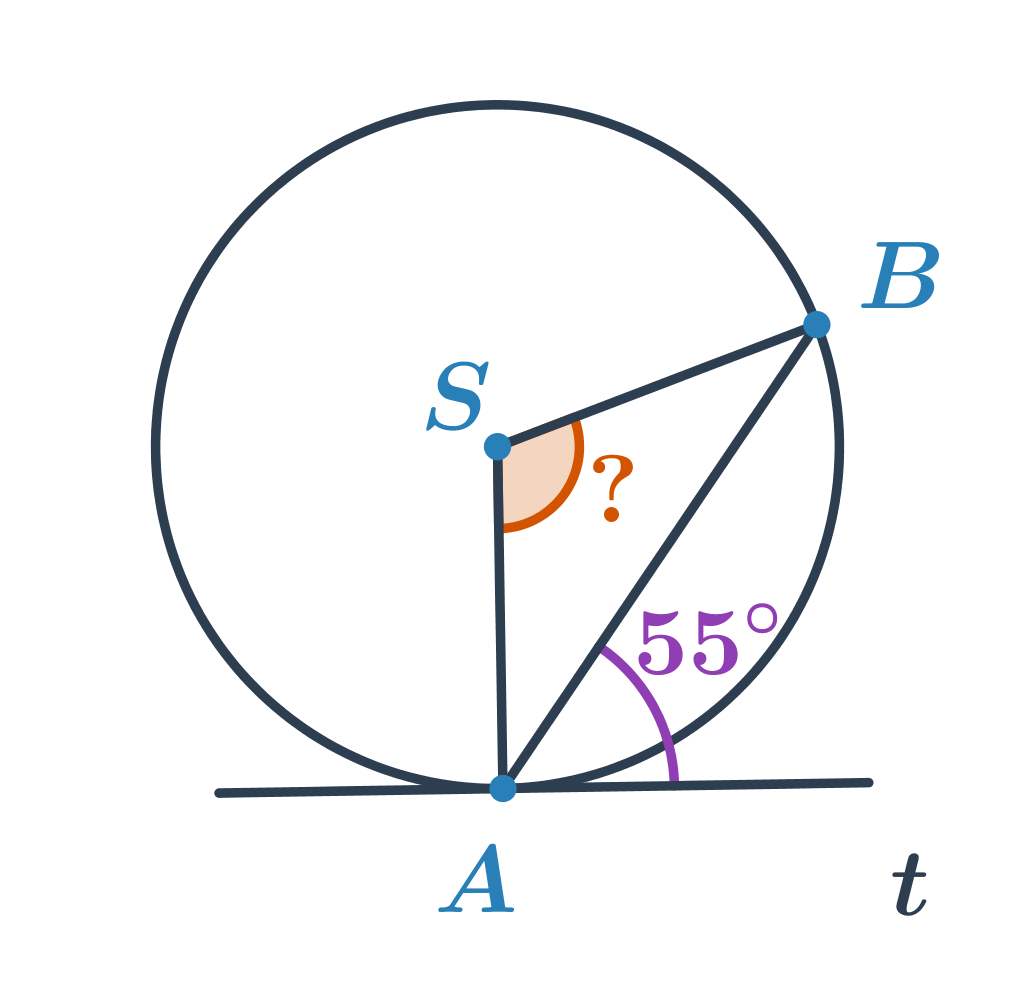
Kąt o mierze 55^\circ jest kątem dopisanym do okręgu. Wiemy, że miary kąta dopisanego i odpowiedniego kąta wpisanego są takie same, czyli wynoszą 55^\circ. Niewiadomy kąt jest kątem środkowym obejmującym mniejszy łuk AB. Jego miara jest dwa razy większa od miary kąta wpisanego, czyli wynosi 2\cdot55^\circ=110^\circ.
Przykład 2: Oblicz miarę kąta
Oblicz miarę kąta zaznaczonego na pomarańczowo.
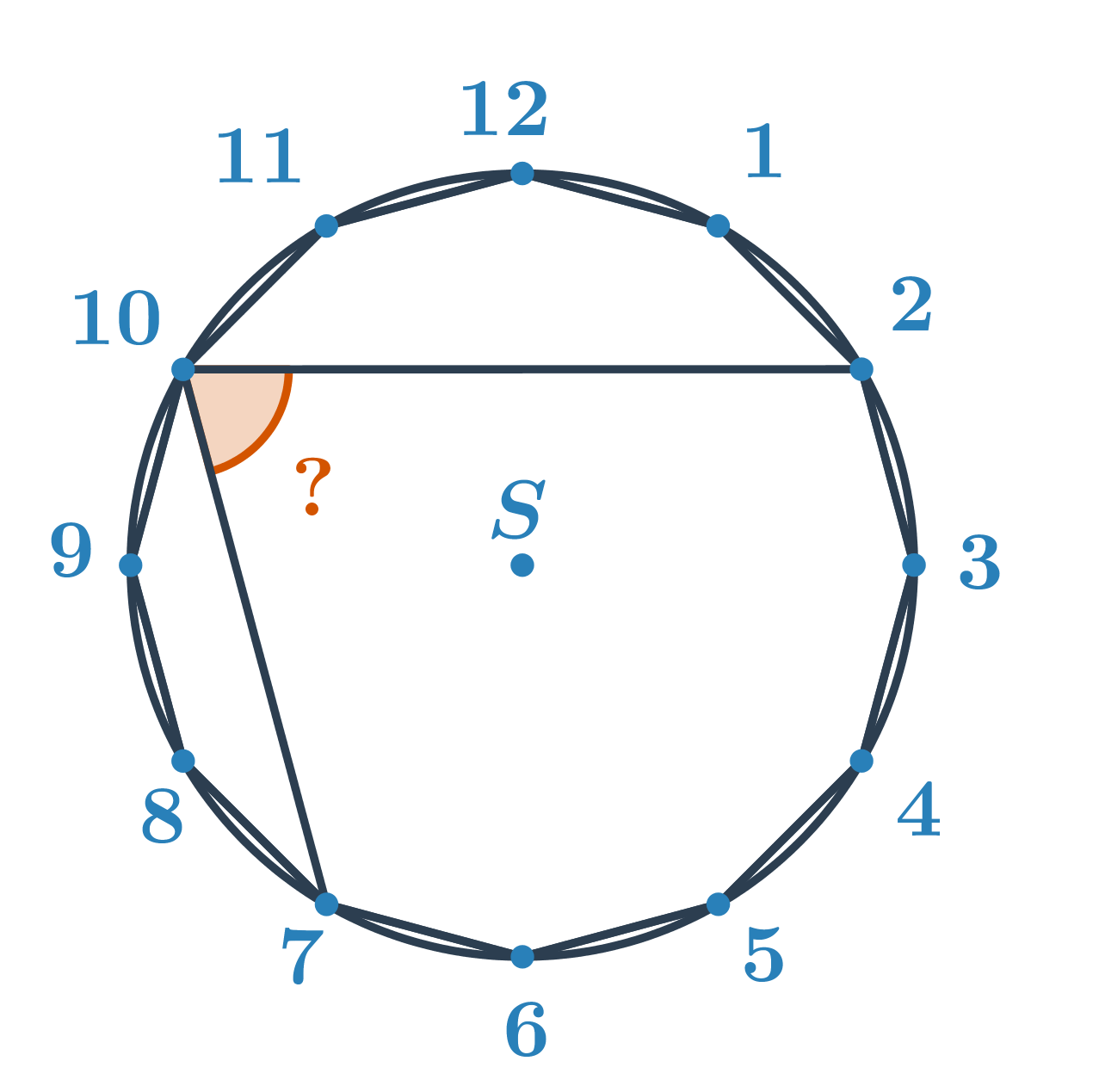
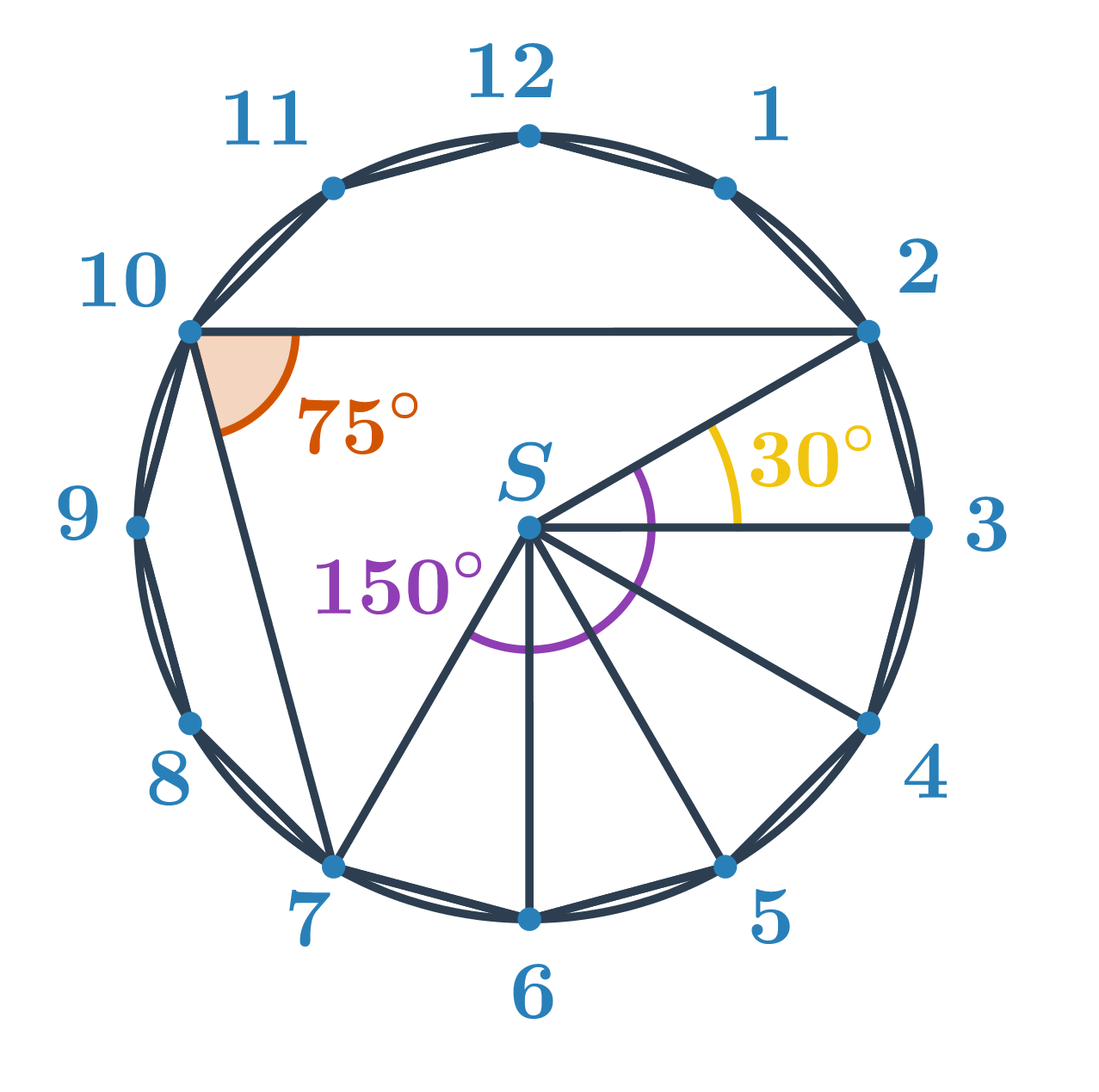
Niewiadomy kąt jest kątem wpisanym nad mniejszym łukiem o końcach w punktach 2 i 7. Obliczamy miarę odpowiedniego kąta środkowego. Z rozdziału kąty i wielokąty wiemy, że miara kąta środkowego n-kąta foremnego wynosi \frac{360^\circ}{n}. Zatem dla dwunastokąta foremnego kąt między odcinkami łączącymi dwa sąsiednie wierzchołki a środkiem \frac{360^\circ}{12}=30^\circ. Kąt środkowy obejmujący łuk 2 i 7 i ma miarę 5\cdot30^\circ=150^\circ. Szukany kąt wpisany jest o połowę mniejszy, czyli jego miara wynosi 150^\circ:2=75^\circ.
