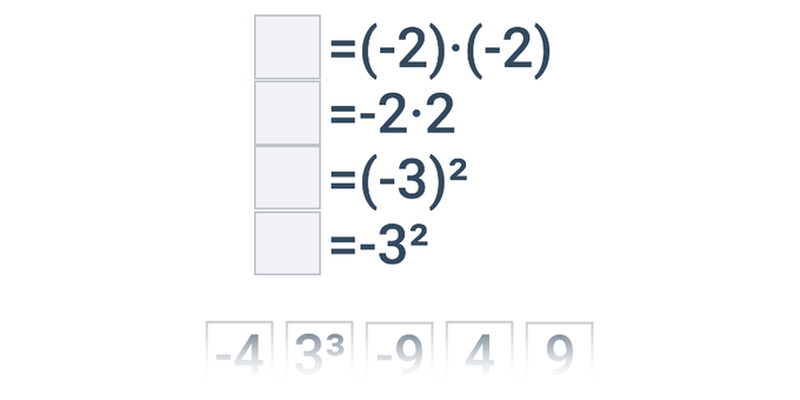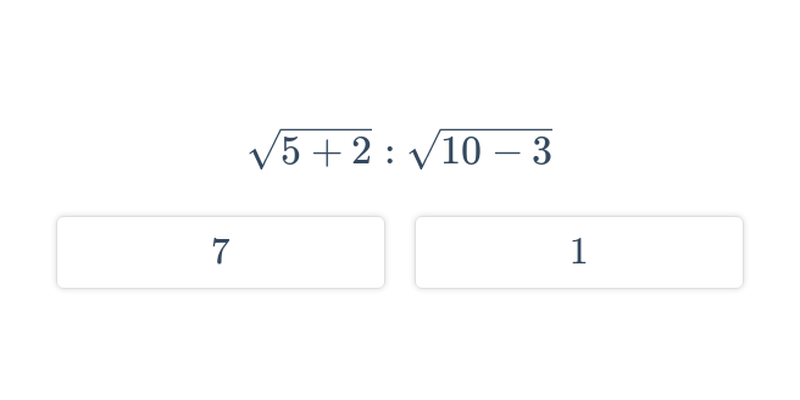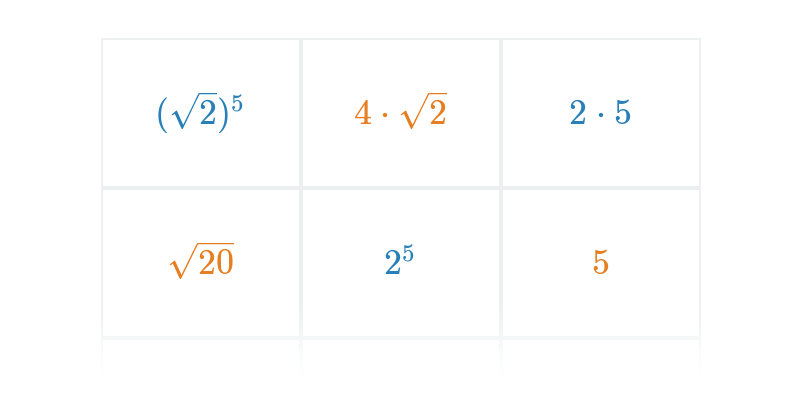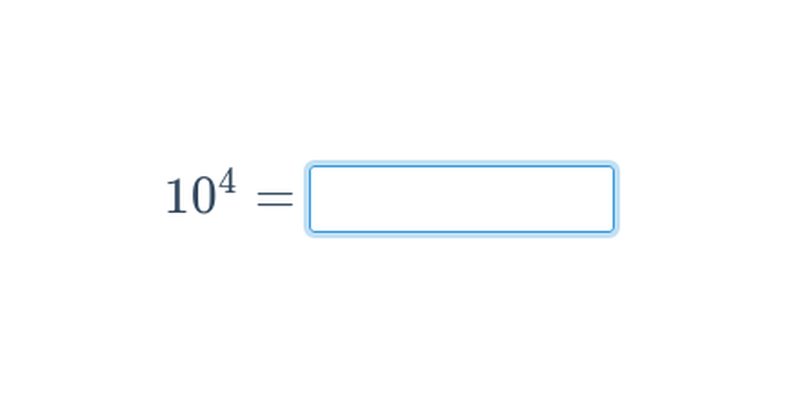Filtruj według klasy
Potęgi i pierwiastki
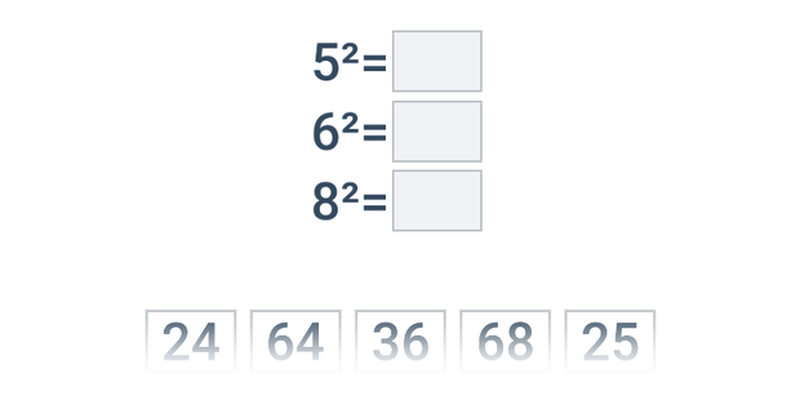
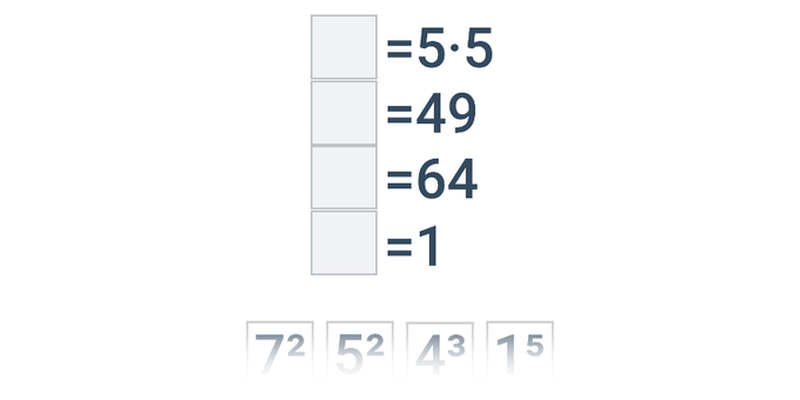
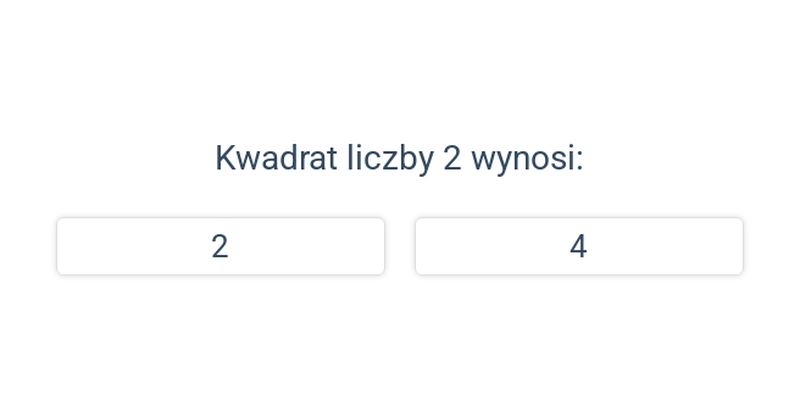
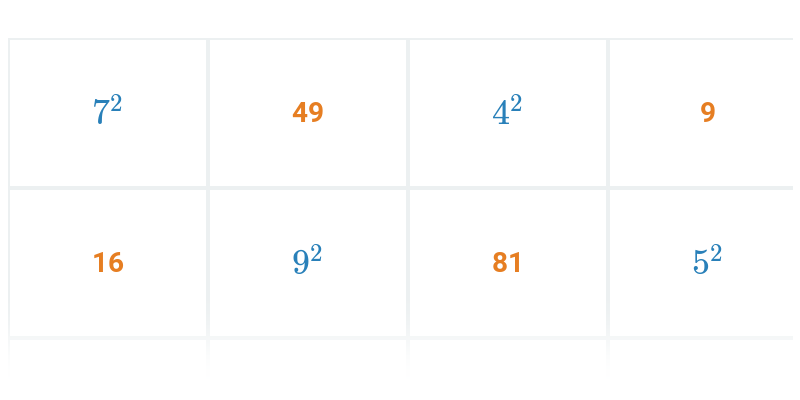
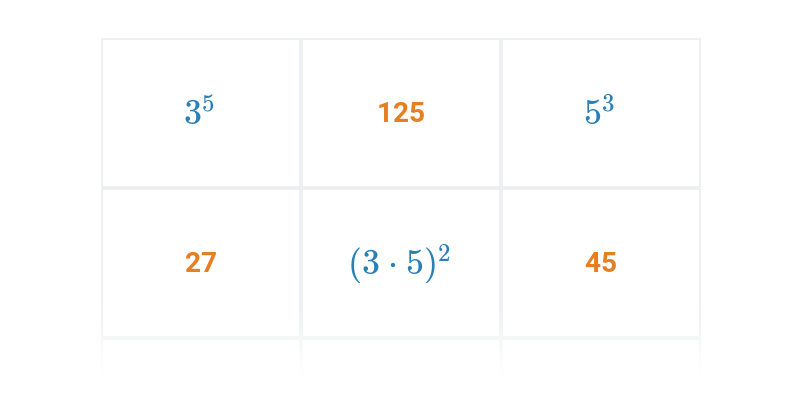
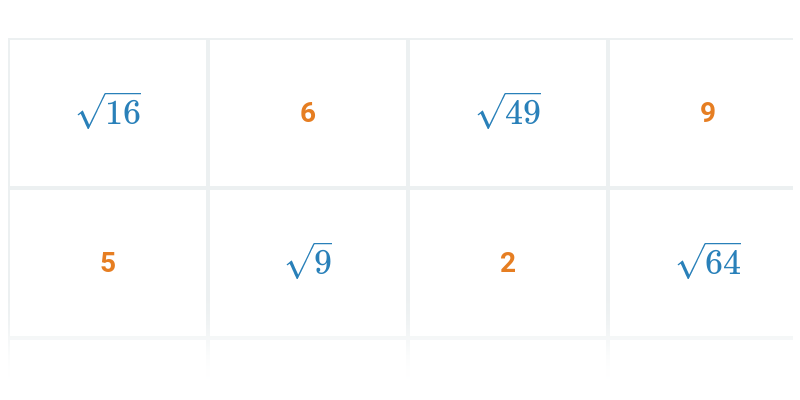
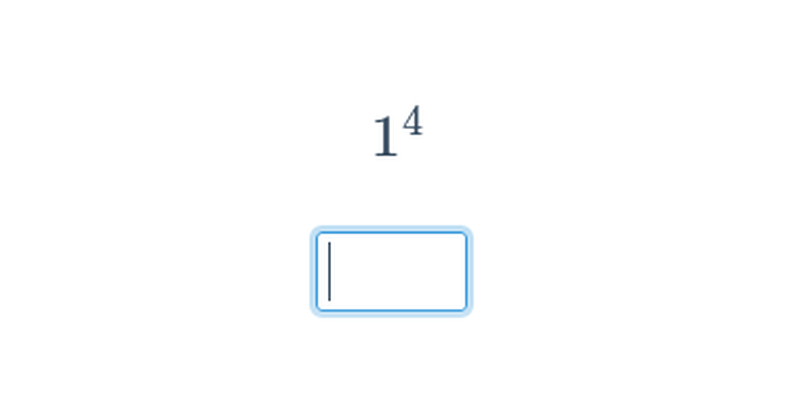
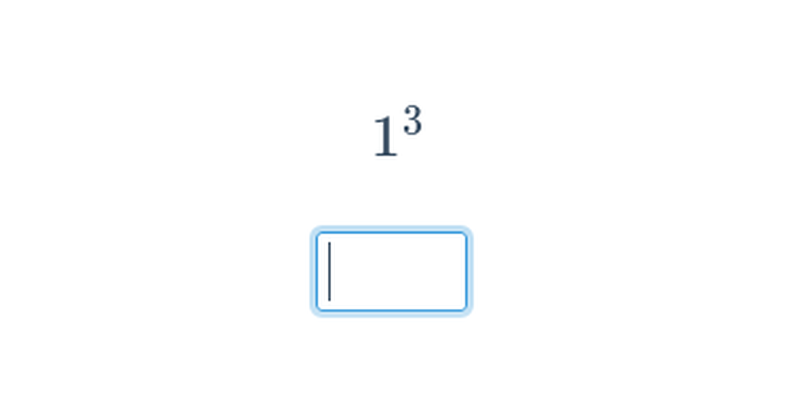
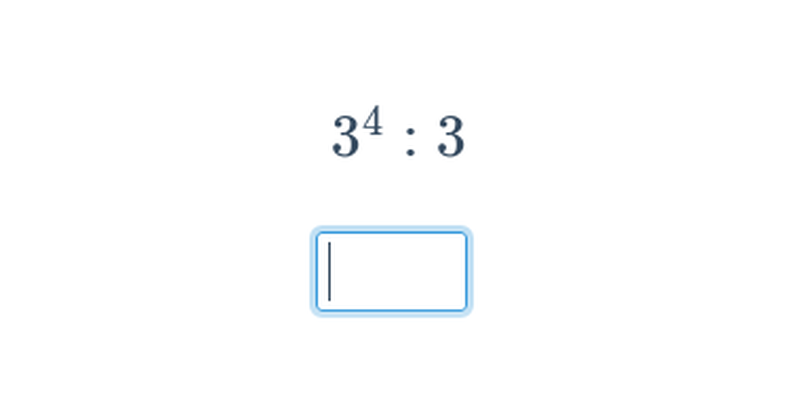
Potęgowanie jest wielokrotnym mnożeniem. Na przykład 3^5 = 3\cdot 3\cdot 3\cdot 3\cdot 3 = 243. Pierwiastkowanie jest działaniem odwrotnym do potęgowania. Na przykład pierwiastek kwadratowy z 36 wynosi 6 (\sqrt{36}=6), ponieważ 6^2 = 6\cdot 6 = 36.
W pierwszej kolejności warto dokładnie przećwiczyć podstawowe potęgi i pierwiastki, a nawet nauczyć się ich na pamięć, ponieważ będą pojawiać się na lekcjach matematyki przy okazji omawiania wielu innych zagadnień, na przykład przy wykonywaniu działań na wielomianach, rozwiązywaniu równań kwadratowych, obliczaniu pola powierzchni i objętości lub wyznaczaniu długości boków w trójkącie.
Kolejnym krokiem będą wyrażenia z potęgami i pierwiastkami.
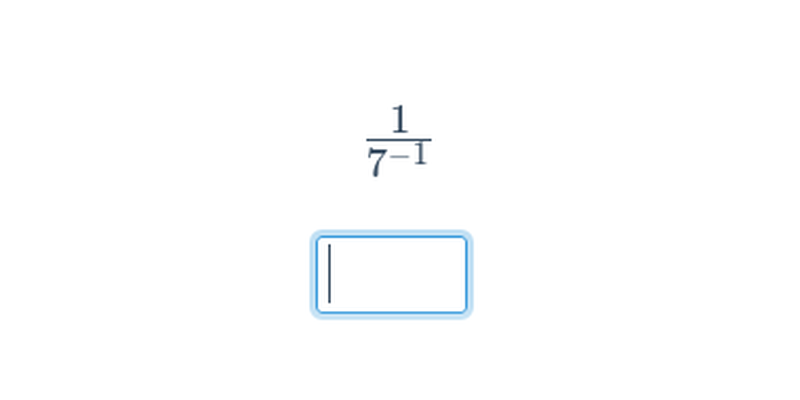
Potęgowanie możemy również zdefiniować dla wykładnika ujemnego. Taką metodę potęgowania stosuje się w notacji naukowej, która pozwala na pracę zarówno z bardzo dużymi, jak i bardzo małymi liczbami. Dlatego jest ona chętnie stosowana w fizyce.
Potęgowanie i pierwiastkowanie możemy również stosować w odniesieniu do ułamków zwykłych i dziesiętnych.
Przesuwanie
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.
Kwadrat i pierwiastek kwadratowy: małe liczby (łatwe) • G1W
Średni czas rozwiązywania: 5 min
Potęgi (łatwe) • FPR
Średni czas rozwiązywania: 5 min
Potęgi (średnie) • FR6
Średni czas rozwiązywania: 5 min
Pierwiastki (średnie) • FSH
Średni czas rozwiązywania: 5 min
Decydowanie
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.
Kwadrat i pierwiastek kwadratowy: małe liczby (łatwe) • GUK
Średni czas rozwiązywania: 5 min
Potęgi liczb 10 i 0,1 (średnie) • GUP
Średni czas rozwiązywania: 5 min
Potęgi (średnie) • EC9
Średni czas rozwiązywania: 3 min
Potęgi (trudne) • EO6
Średni czas rozwiązywania: 6 min
Pierwiastki (łatwe) • GT3
Średni czas rozwiązywania: 3 min
Pierwiastki (średnie) • ENS
Średni czas rozwiązywania: 4 min
Pierwiastki (trudne) • FJ6
Średni czas rozwiązywania: 5 min
Wyrażenia z potęgami i pierwiastkami (średnie) • EKP
Średni czas rozwiązywania: 5 min
Wyrażenia z potęgami i pierwiastkami (trudne) • E4H
Średni czas rozwiązywania: 5 min
Potęgi liczb ujemnych (trudne) • ENU
Średni czas rozwiązywania: 5 min
Notacja naukowa (średnie) • E4J
Średni czas rozwiązywania: 5 min
Potęgi i pierwiastki : miks przykładów (średnie) • ENT
Średni czas rozwiązywania: 5 min
Potęgi i pierwiastki : miks przykładów (trudne) • EP2
Średni czas rozwiązywania: 5 min
Memory
Szukanie pasujących par.
Potęgi (średnie) • E4E
Średni czas rozwiązywania: 2 min
Potęgi (trudne) • E9S
Średni czas rozwiązywania: 5 min
Pierwiastki (średnie) • E4F
Średni czas rozwiązywania: 2 min
Pierwiastki (trudne) • E9T
Średni czas rozwiązywania: 5 min
Wyrażenia z potęgami i pierwiastkami (średnie) • E93
Średni czas rozwiązywania: 5 min
Potęgi liczb ujemnych (trudne) • E4G
Średni czas rozwiązywania: 5 min
Potęgi i pierwiastki : miks przykładów (średnie) • EBO
Średni czas rozwiązywania: 5 min
Wpisywanie odpowiedzi
Ćwiczenie, w którym wpisujesz odpowiedź na klawiaturze.
Kwadrat i pierwiastek kwadratowy: małe liczby (łatwe) • GUL
Średni czas rozwiązywania: 5 min
Potęgi liczb 10 i 0,1 (średnie) • GUR
Średni czas rozwiązywania: 5 min
Potęgi (łatwe) • GUJ
Średni czas rozwiązywania: 5 min
Potęgi (średnie) • EAP
Średni czas rozwiązywania: 6 min
Potęgi (trudne) • EO9
Średni czas rozwiązywania: 5 min
Pierwiastki (łatwe) • GTU
Średni czas rozwiązywania: 3 min
Pierwiastki (średnie) • ENP
Średni czas rozwiązywania: 5 min
Wyrażenia z potęgami i pierwiastkami (średnie) • EBF
Średni czas rozwiązywania: 5 min
Potęgi liczb ujemnych (trudne) • ENV
Średni czas rozwiązywania: 5 min
Potęgi i pierwiastki : miks przykładów (średnie) • ENR
Średni czas rozwiązywania: 5 min
Potęgi i pierwiastki : miks przykładów (trudne) • FBP
Średni czas rozwiązywania: 5 min
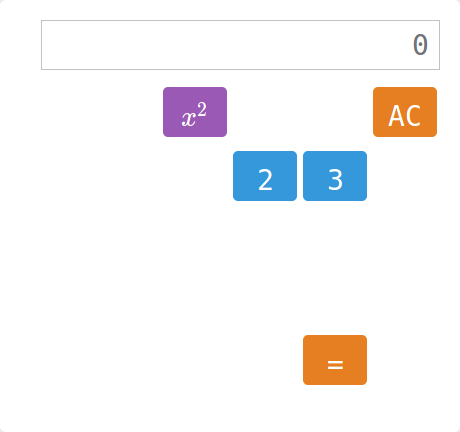
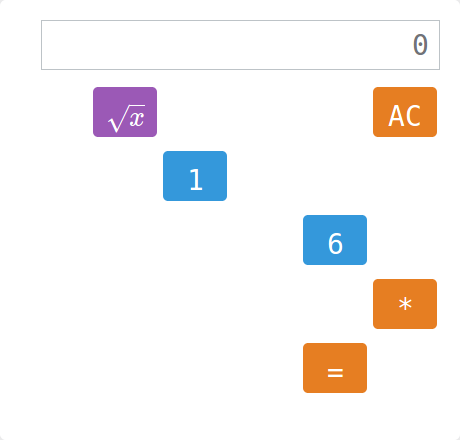
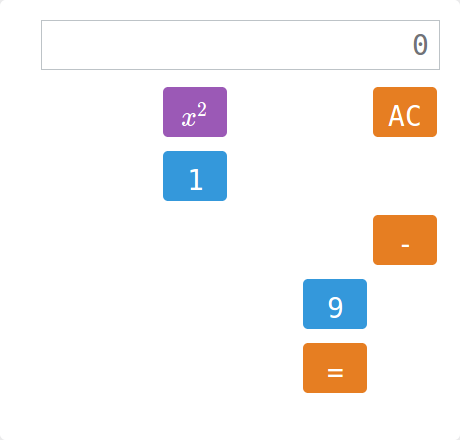
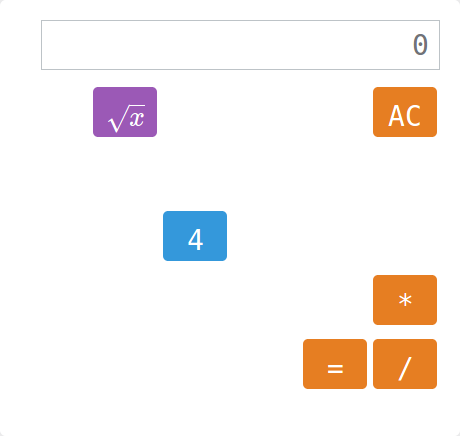
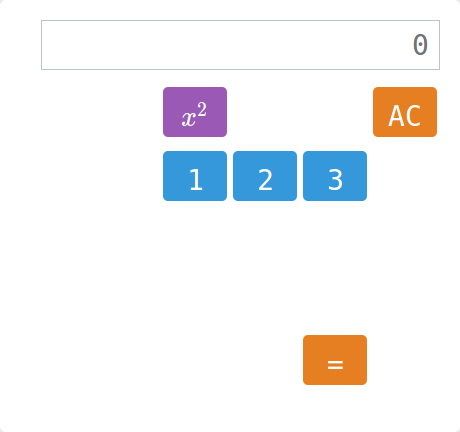
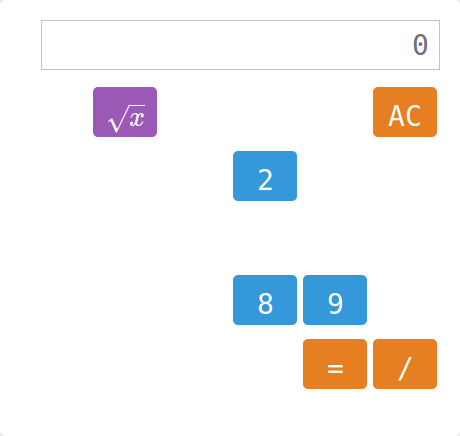
Kalkulator
Zadanie polega na tym, by na wyświetlaczu kalkulatora wygenerować podane liczby. Trudność polega na tym, że brakuje niektórych przycisków…
