Współrzędne wektora

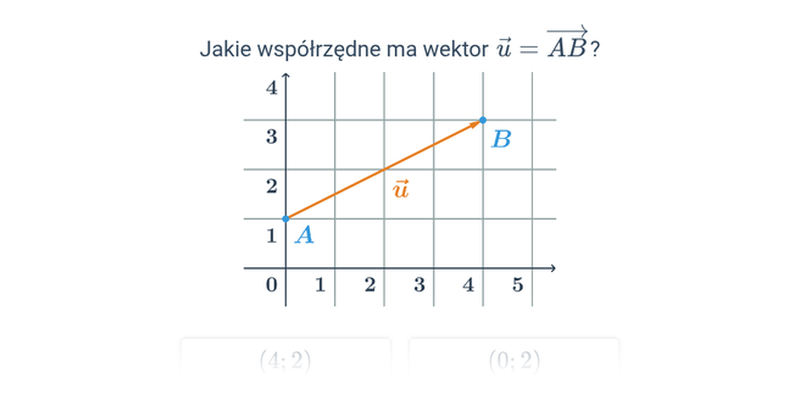
Wiemy już, że wektor to uporządkowana para punktów. Jeżeli dane są współrzędne punktów A=[a_1;a_2] i B=[b_1;b_2], to współrzędne wektora \overrightarrow{AB} określa wzór \overrightarrow{AB}=B-A=(b_1-a_1;b_2-a_2).

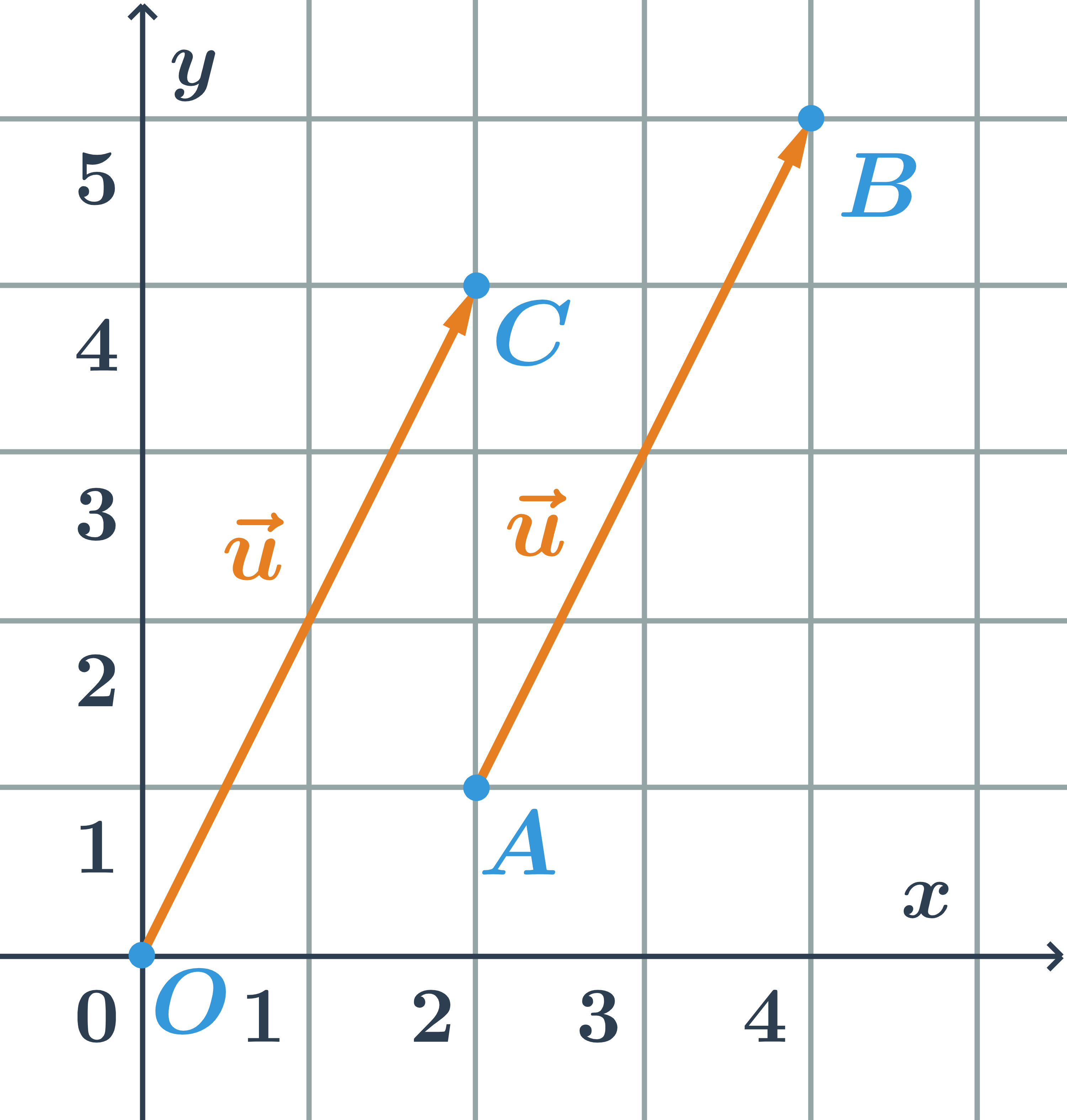
Współrzędne wektora \overrightarrow{AB}

Spróbujmy przesunąć wektor \overrightarrow{AB} na początek układu współrzędnych. Aby to zrobić, musimy przesunąć go o dwie kratki w lewo i o jedną kratkę w dół.
Punkt A znajdzie się wówczas w miejscu punktu O, a punkt B w miejscu punktu C. Takie przesunięcie możemy wyrazić w następujący sposób:
- A przesuwa się na [2-2;1-1]=[0;0]
- B przesuwa się na [4-2;5-1]=[2;4]
Zatem współrzędne wektora przestawionego na rysunku to: \vec{u}=\overrightarrow{AB}=\overrightarrow{OC}=(2;4)