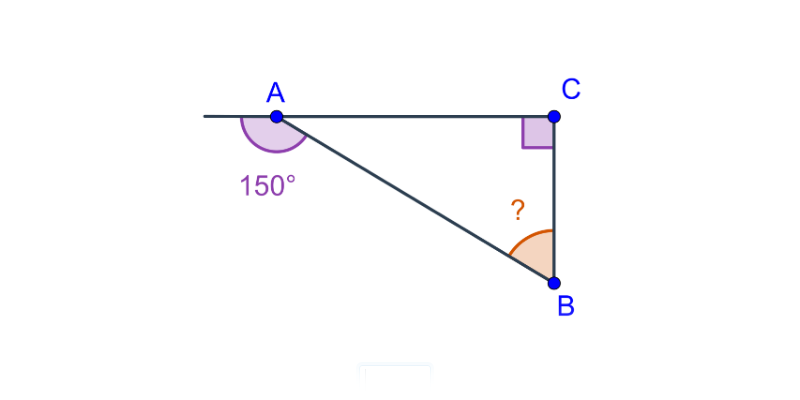
Kąty w trójkącie
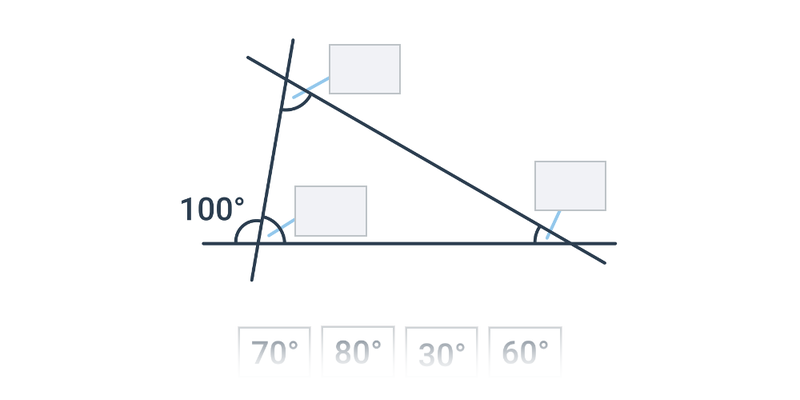
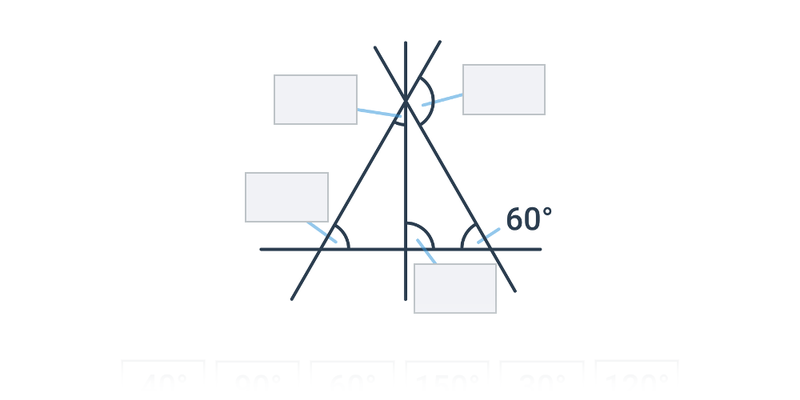
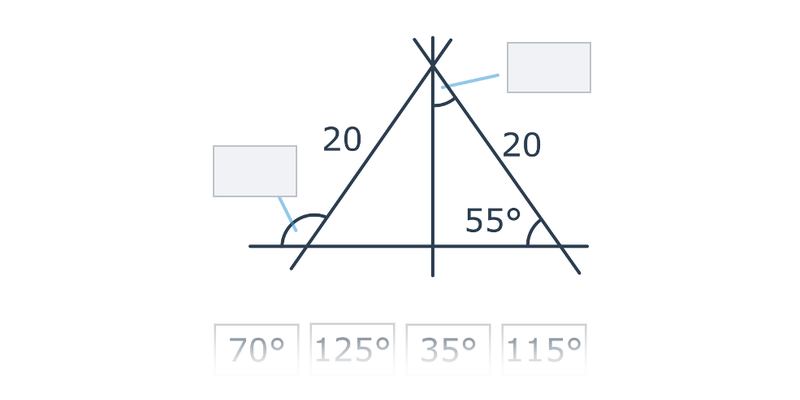
Aby obliczyć miarę nieznanego kąta w trójkącie, korzystamy z podstawowej zasady, która mówi, że suma kątów wewnętrznych w trójkącie wynosi 180°.
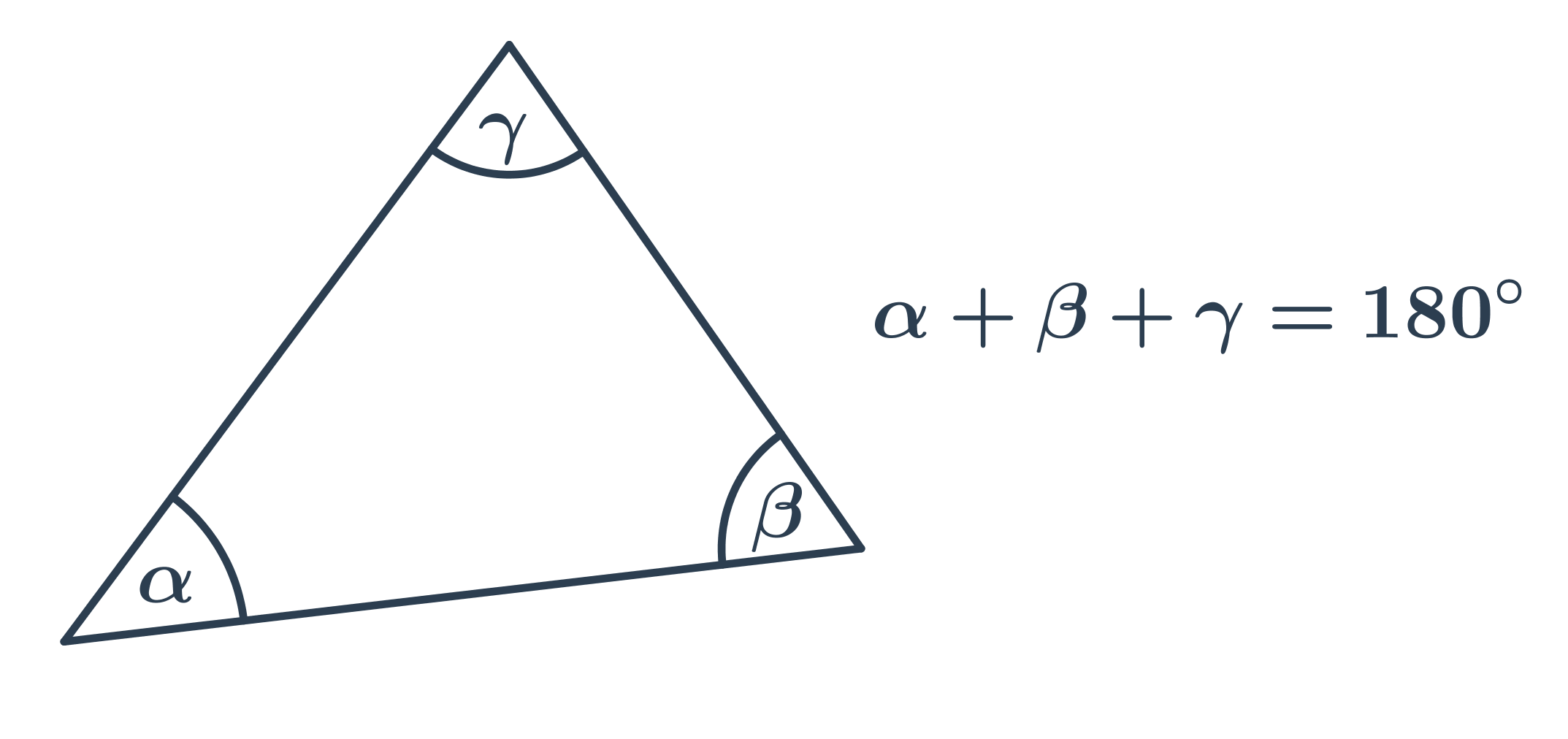
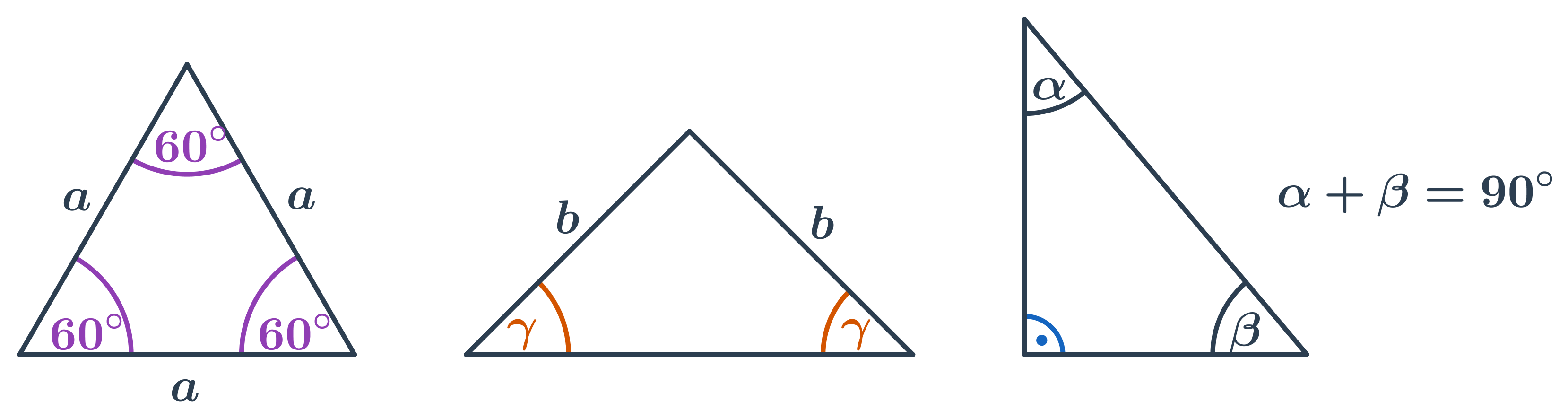
Szczególne przypadki:
- W trójkącie równobocznym wszystkie kąty mają 60°.
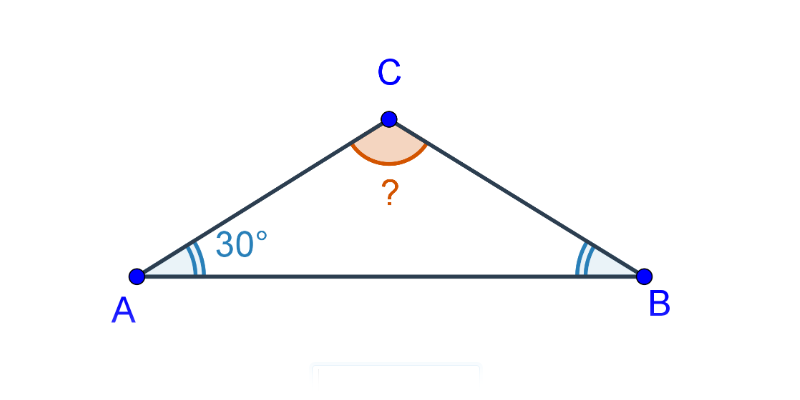
- W trójkącie równoramiennym obydwa kąty przy podstawie są takie same.
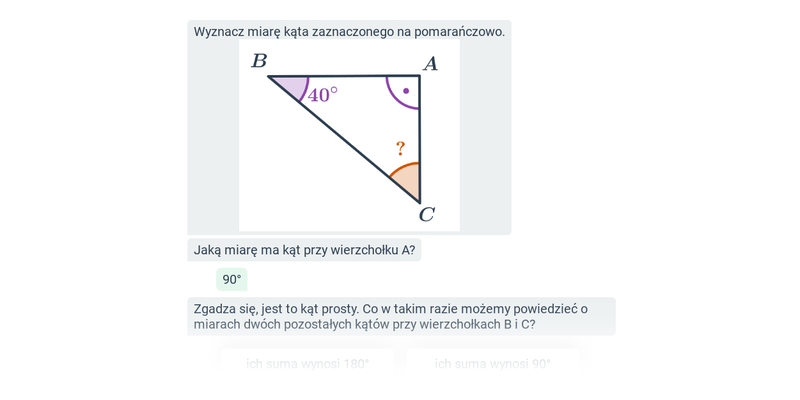
- W trójkącie prostokątnym jeden kąt ma 90°, a suma dwu pozostałych kątów również wynosi 90°.
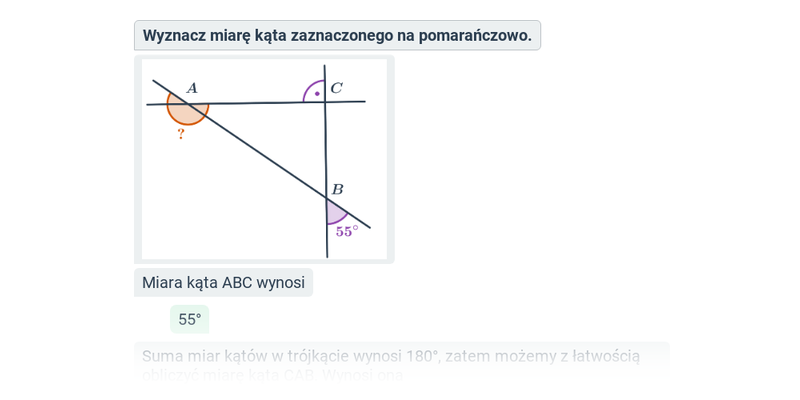
Do obliczenia miary kąta możemy również wykorzystać kąty wierzchołkowe i przyległe.
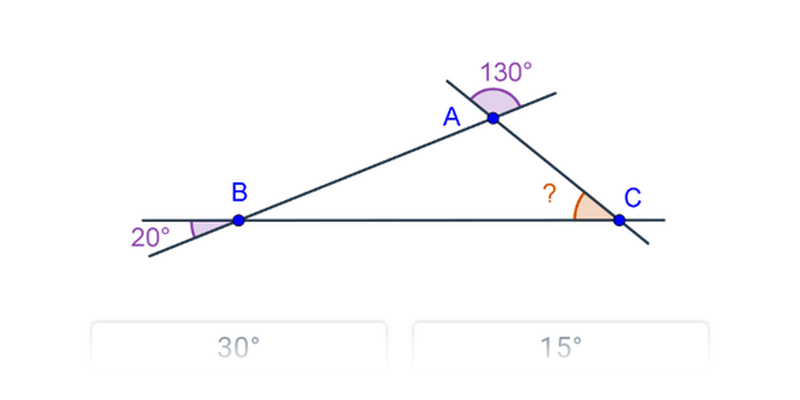
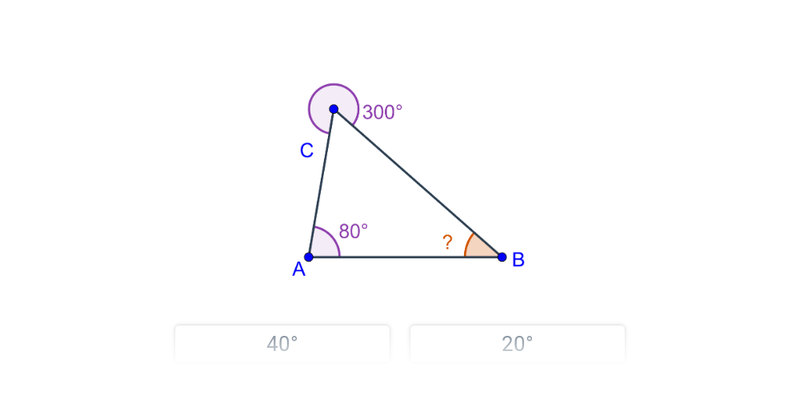
Przykład: Oblicz miarę kąta zaznaczonego na pomarańczowo.
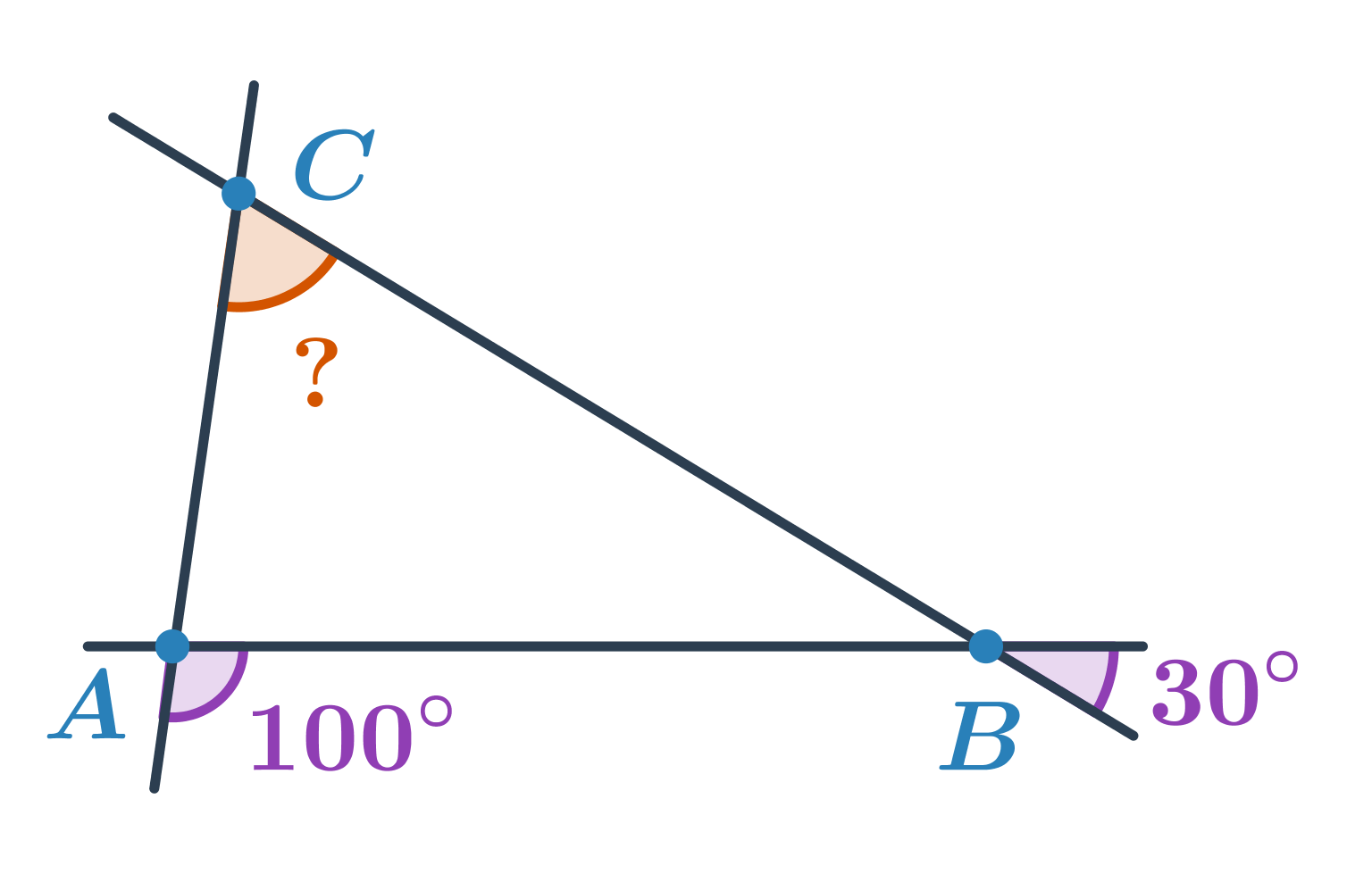
Kąt przy wierzchołku B tworzy parę kątów wierzchołkowych z kątem o mierze 30°, zatem będzie miał 30°. Z kolei kąt przy wierzchołku A tworzy parę kątów przyległych z kątem o mierze 100°, zatem będzie miał 180°-100°=80°. Obliczamy miarę niewiadomego kąta przy wierzchołku C: 180°-80°-30°=70°
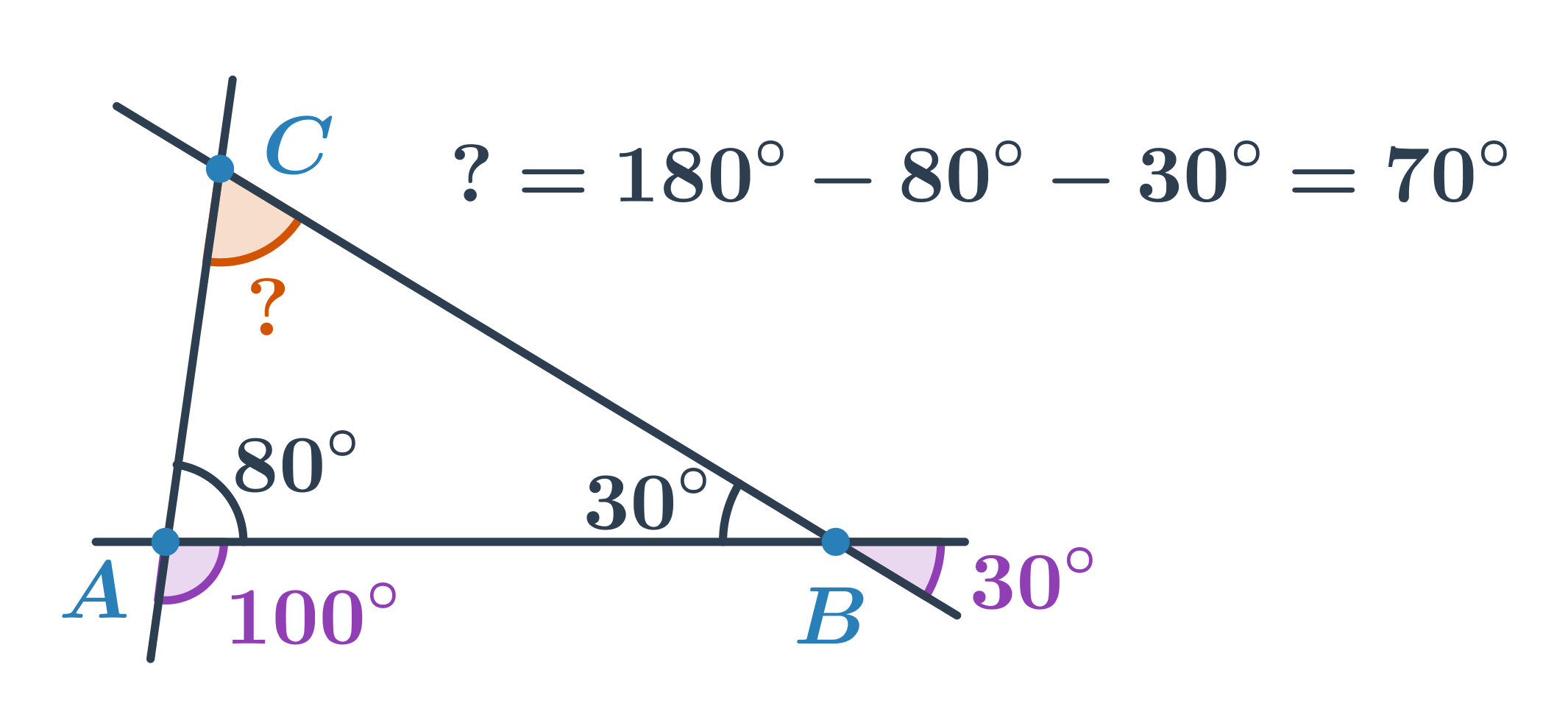
Przesuwanie
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.
Decydowanie
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.