Dziękujemy za ocenę.

Podobieństwo

Dwie figury geometryczne są podobne, jeżeli mają taki sam kształt (niezależnie od wielkości). Na poniższym rysunku figury podobne mają ten sam kolor:

Dokładniej rzecz biorąc, figury są podobne, jeżeli możemy przekształcić jedną figurę na drugą, a to poprzez równomierne zmiejszenie lub zwiększenie oraz przesunięcie, obrócenie lub odwrócenie.

Podobieństwo zachowuje miary kątów i stosunek długości.

Stosunek długości odpowiednich odcinków w obu figurach nazywamy skalą podobieństwa.

Przykład 1

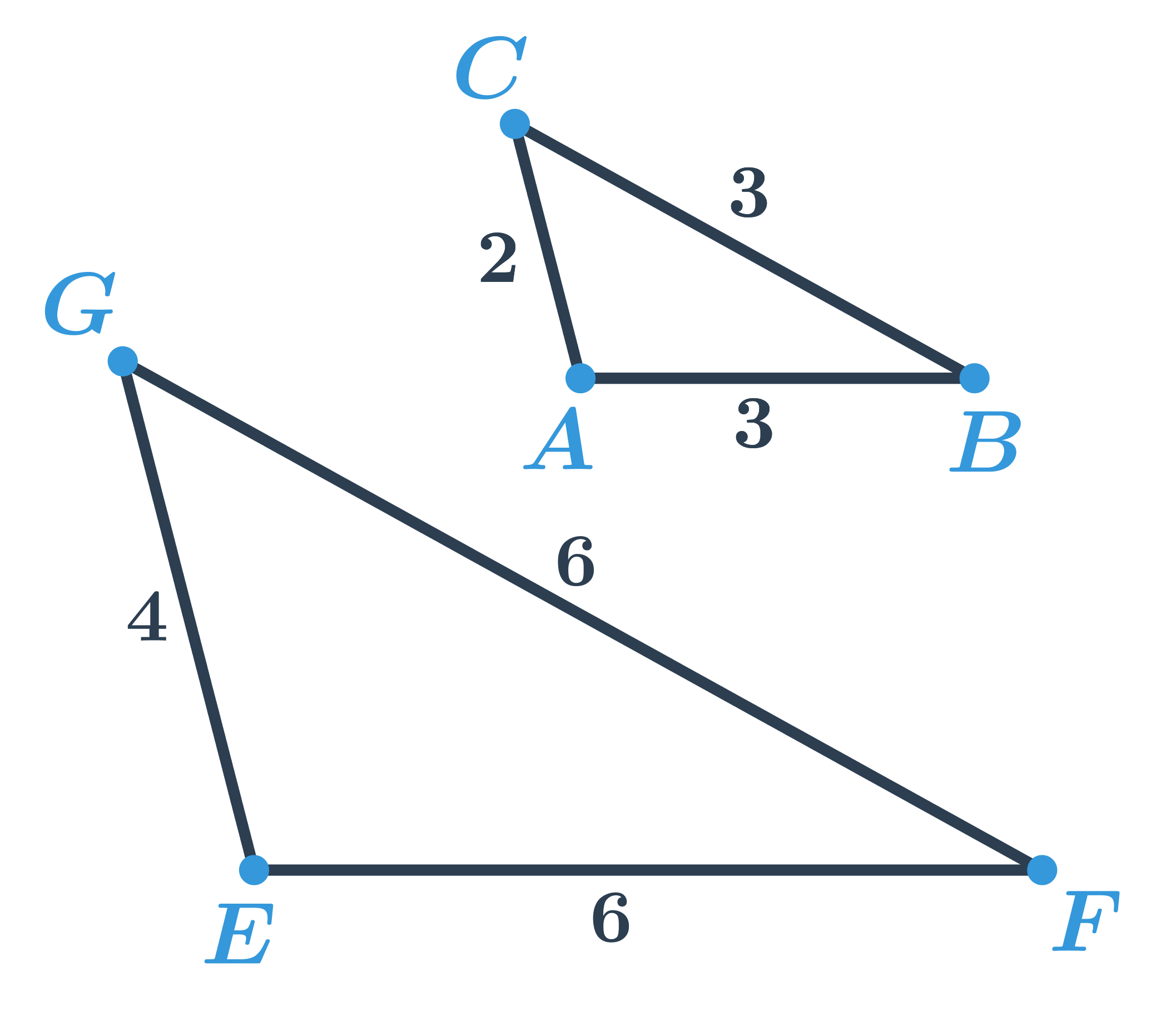
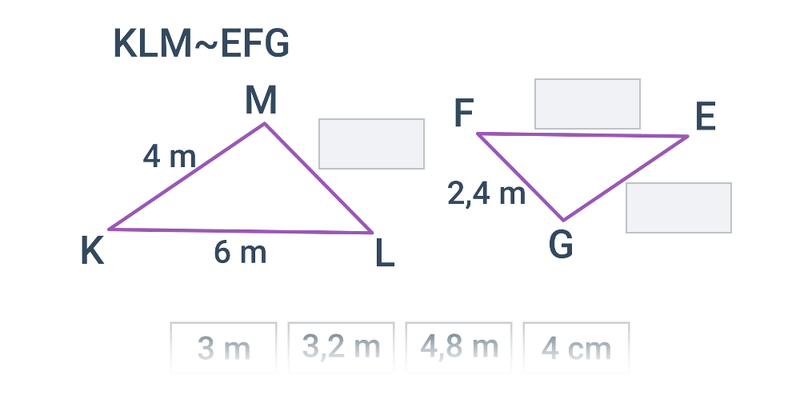
Trójkąty ABC i EFG są podobne, ponieważ stosunek długości odpowiednich boków jest taki sam:

\frac{EF}{AB}=\frac{6}{3}=2
\frac{FG}{BC}=\frac{6}{3}=2
\frac{GE}{CA}=\frac{4}{2}=2

Zapiszemy \bigtriangleup EFG\sim \bigtriangleup ABC, skala podobieństwa wynosi 2.

Przykład 2

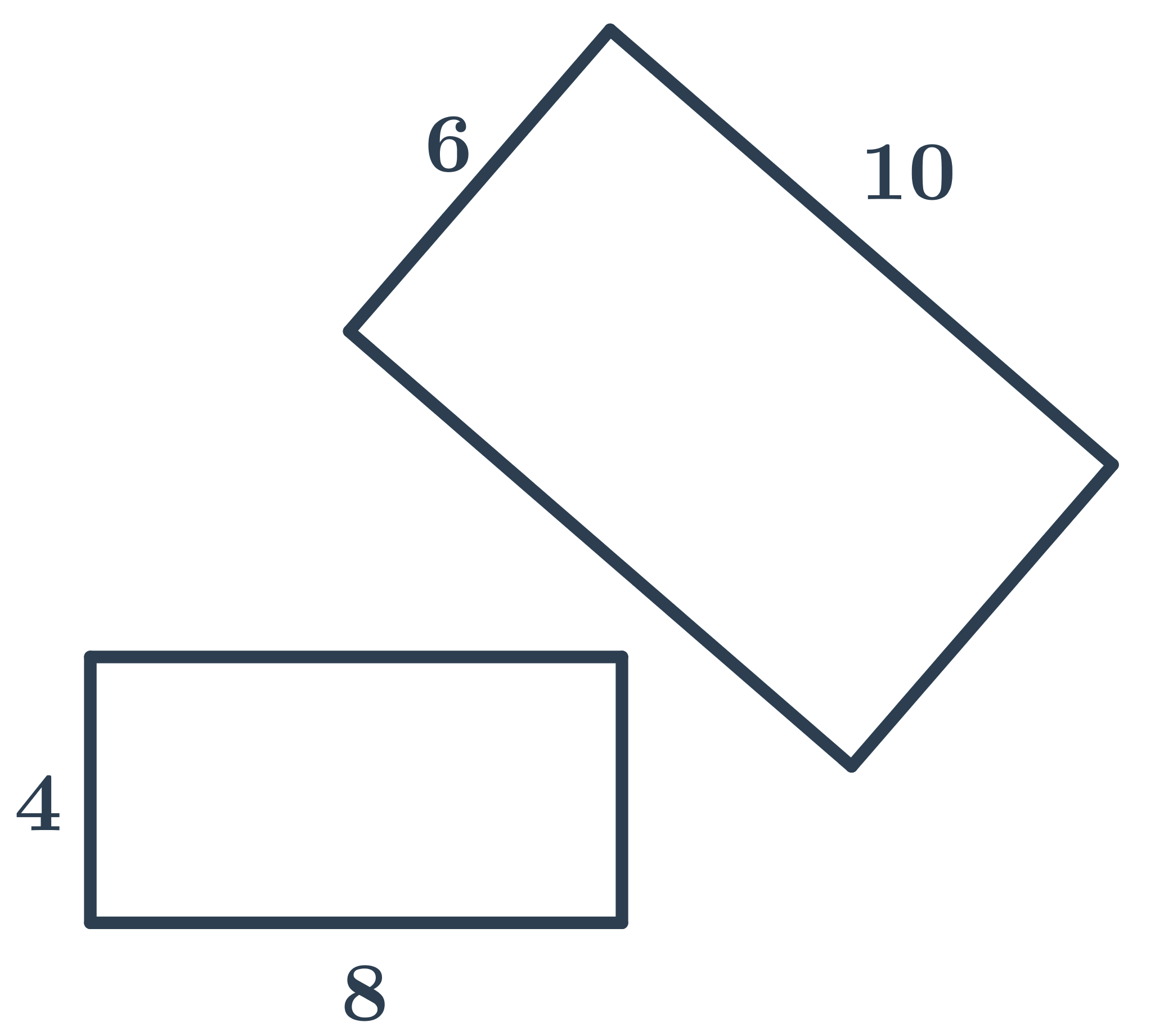
Prostokąty przedstawione na rysunku nie są podobne, ponieważ stosunek długości odpowiednich boków nie jest taki sam:

stosunek dłuższych boków wynosi \frac{10}{8}=\frac{5}{4}
stosunek krótszych boków wynosi \frac{6}{4}=\frac{3}{2}

Przesuwanie

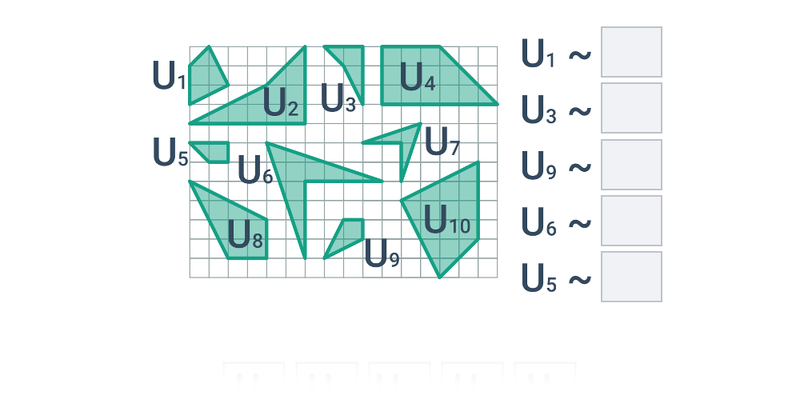
Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.

Podobieństwo

Podobieństwo na kratce

Podobieństwo na kratce

Przesuwanie • średnie

Podobieństwo na kratce

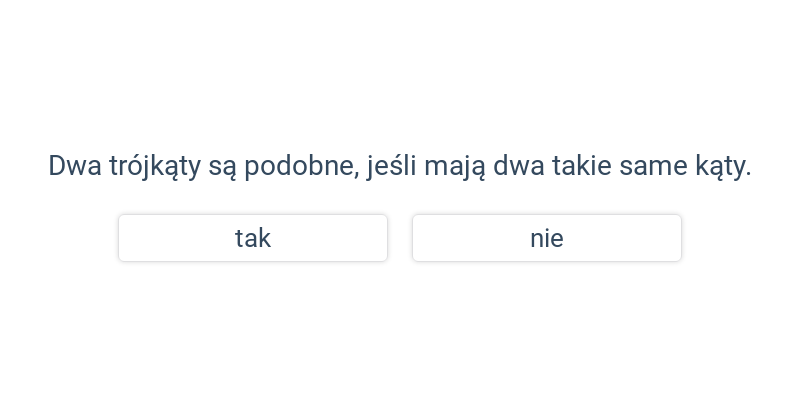
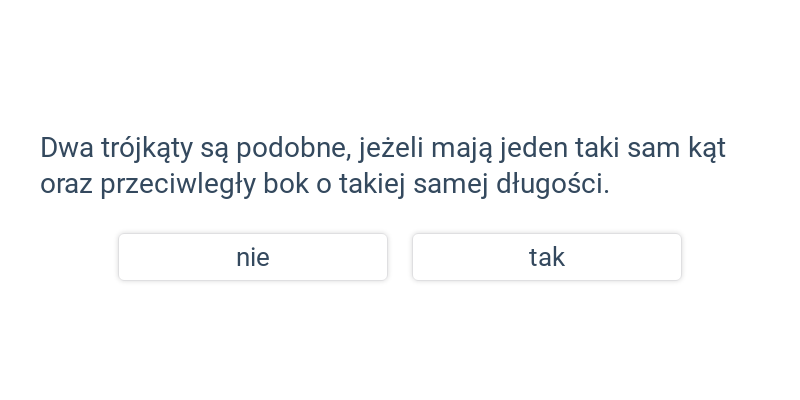
Decydowanie

Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.

Podobieństwo

Podobieństwo

Decydowanie • trudne

Podobieństwo

Kratki

Niesztampowe ćwiczenie do nauki geometrii z prostym sterowaniem.

Podobieństwo

Podobieństwo

Kratki

Podobieństwo

Roboty

Wyścigi z robotami. Proste sterowanie za pomocą wyboru poprawnej odpowiedzi.

Podobieństwo

NAPISZ DO NAS

Twoja wiadomość została wysłana. Dziękujemy.

Napisz do nas

Jesteś w kropce?

Najpierw przejrzyj najczęściej zadawane pytania:

FAQ

Czego dotyczy wiadomość?

Po prostu wiadomość Treść Sterowanie Logowanie Licencja