Dziękujemy za ocenę.

Geometria analityczna

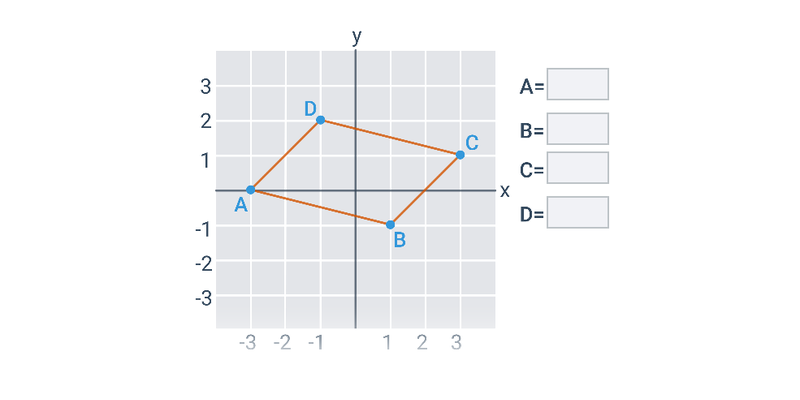
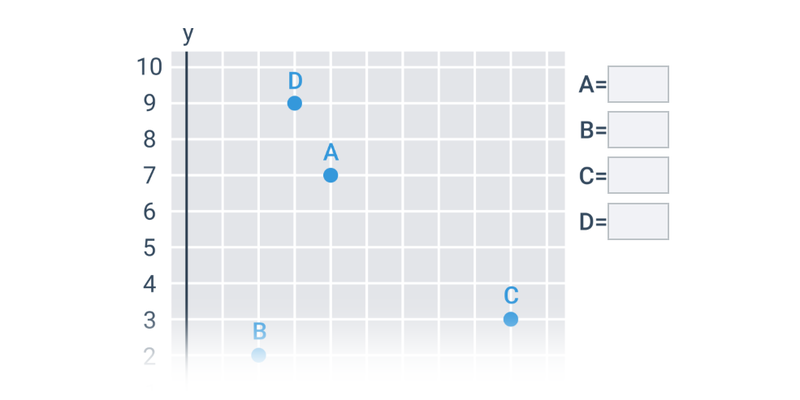
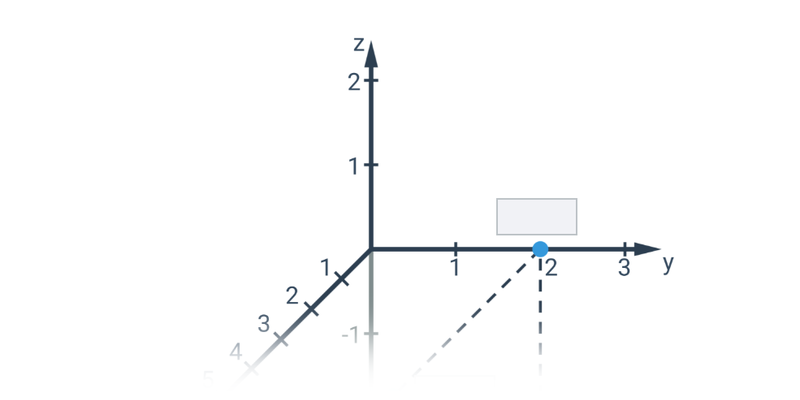
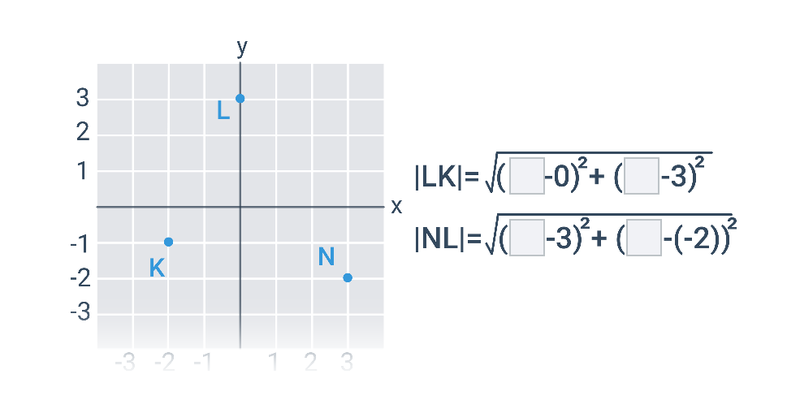Geometria analityczna łączy geometrię i algebrę. Pozwala nam przedstawić problemy geometryczne w postaci algebraicznej i rozwiązywać je za pomocą równań.

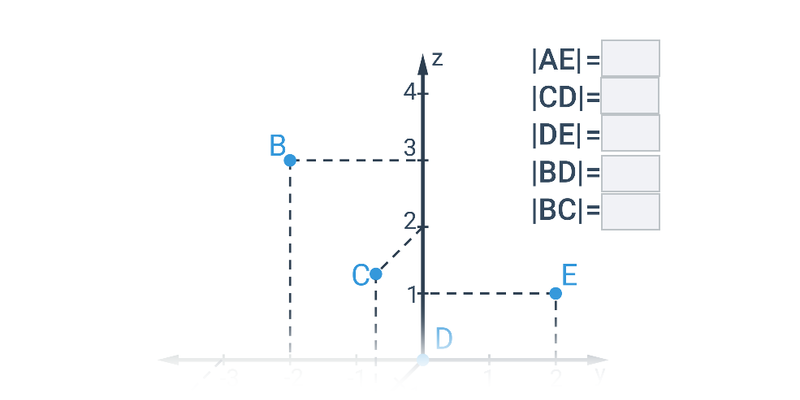
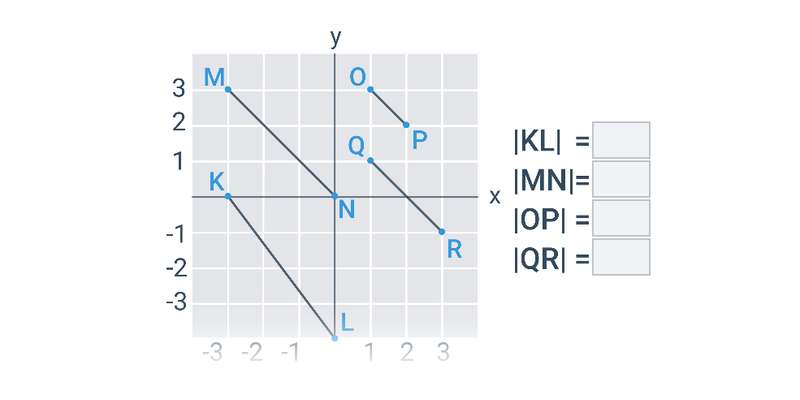
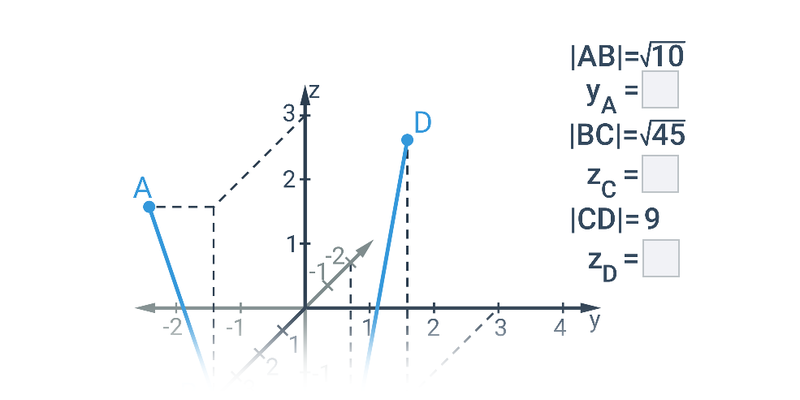
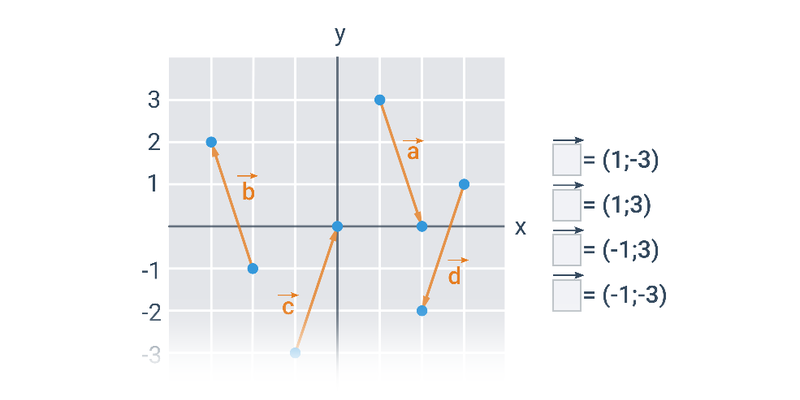
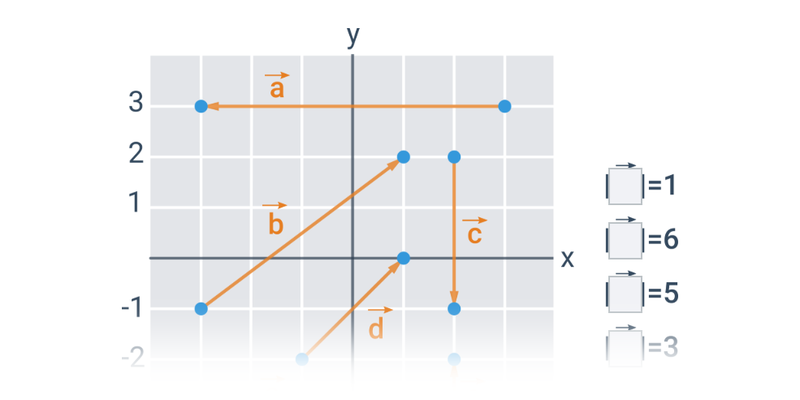
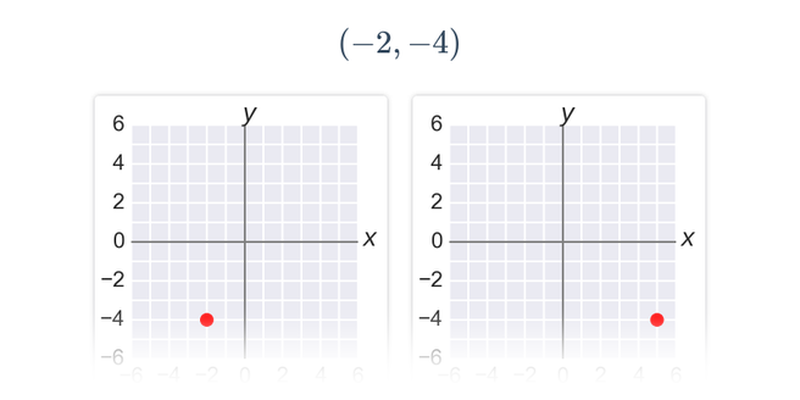
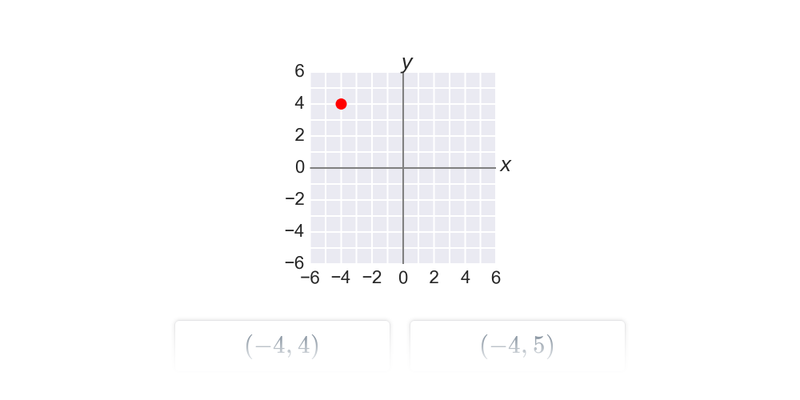
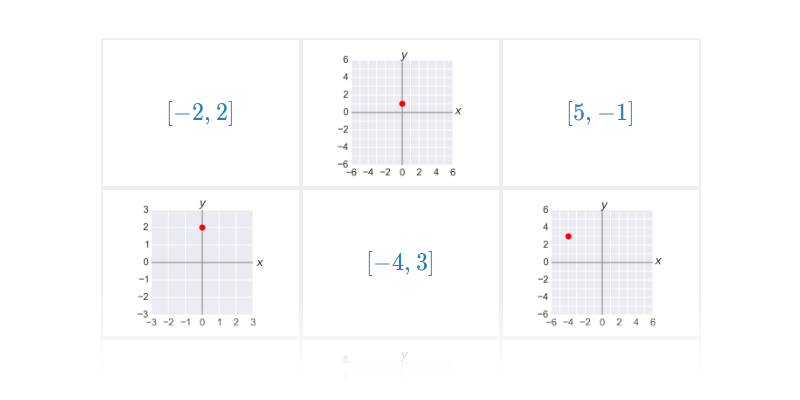
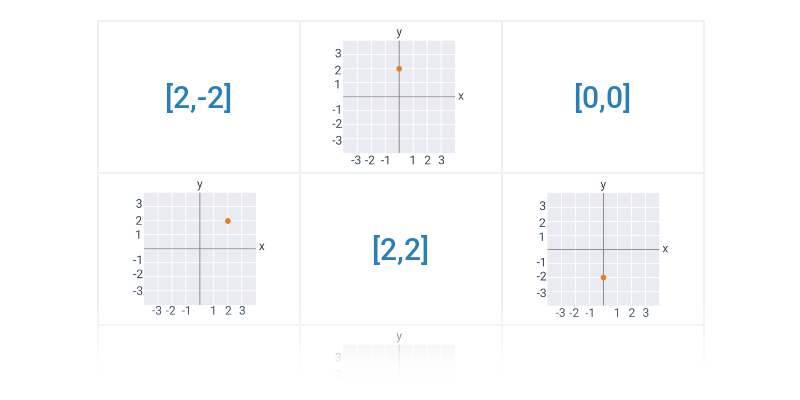
Najprostszymi obiektami, które można opisać analitycznie, są punkty, odcinki i wektory na płaszczyźnie lub w przestrzeni. Gdy już potrafimy operować wektorami, możemy użyć ich na przykład do opisu prostej lub płaszczyzny.

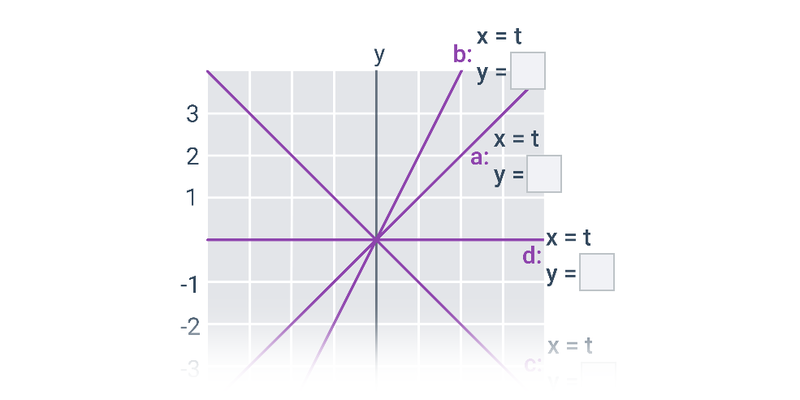
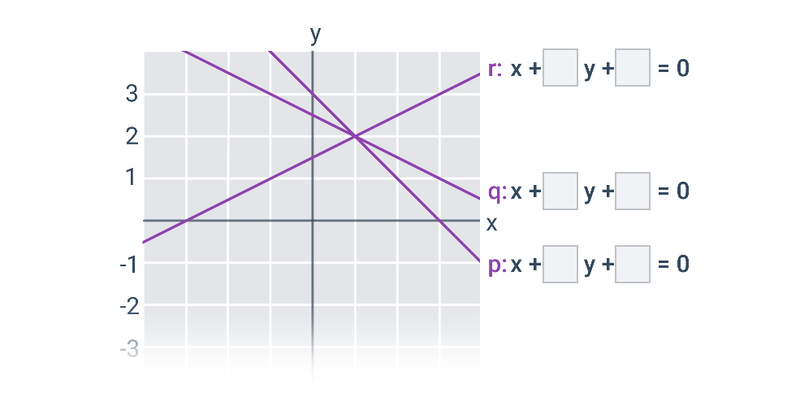
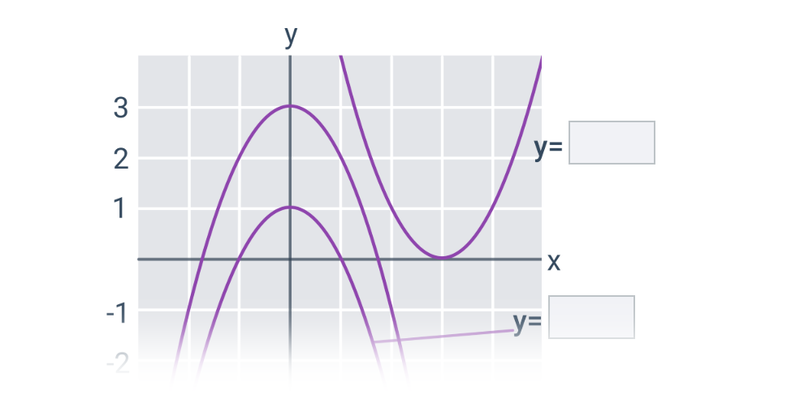
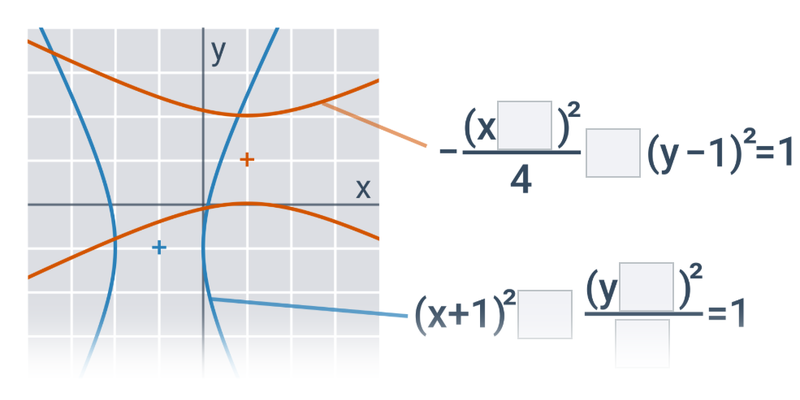
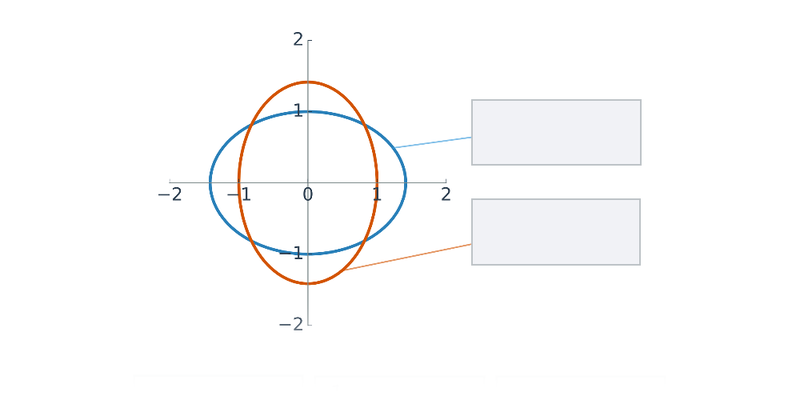
W przypadku prostych i płaszczyzn nadal mamy do czynienia z obiektami, które można opisać za pomocą równań liniowych lub układów równań liniowych. Jeśli zajmiemy się również równaniami kwadratowymi, będziemy w stanie opisać krzywe stożkowe na płaszczyźnie, takie jak okrąg, elipsa, parabola czy hiperbola.

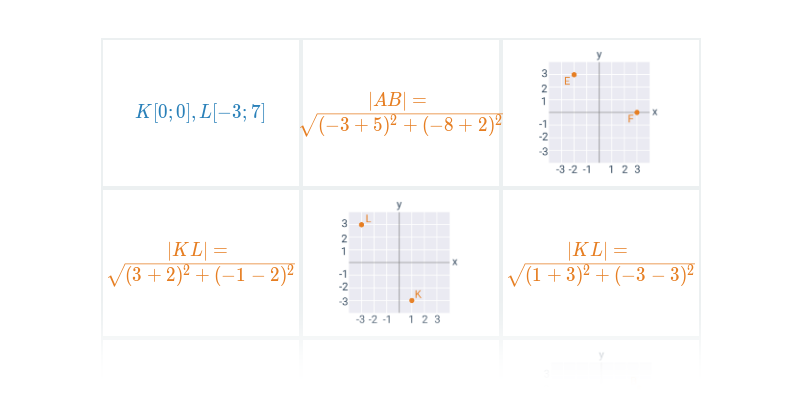
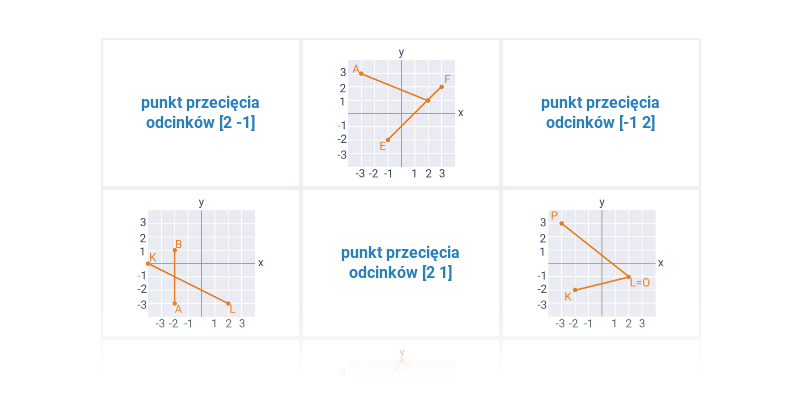
Dwa ważne typy problemów, które rozwiązujemy w ramach geometrii analitycznej, to zadania na położenie, w których badamy wzajemne położenie obiektów geometrycznych, oraz zadania na odległość, w których obliczamy konkretną wartość liczbową wyniku, taką jak na przykład odległość między dwoma punktami lub kąt zawarty między dwiema przecinającymi się prostymi.

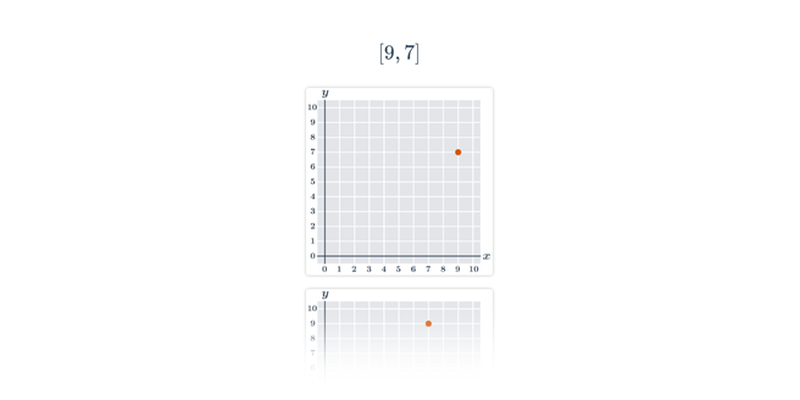
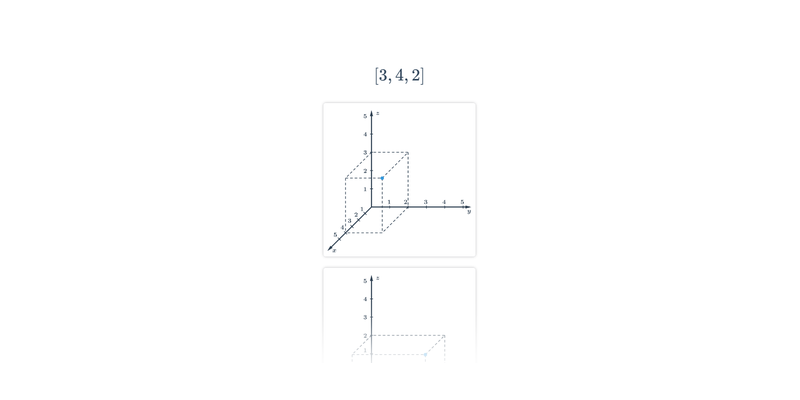
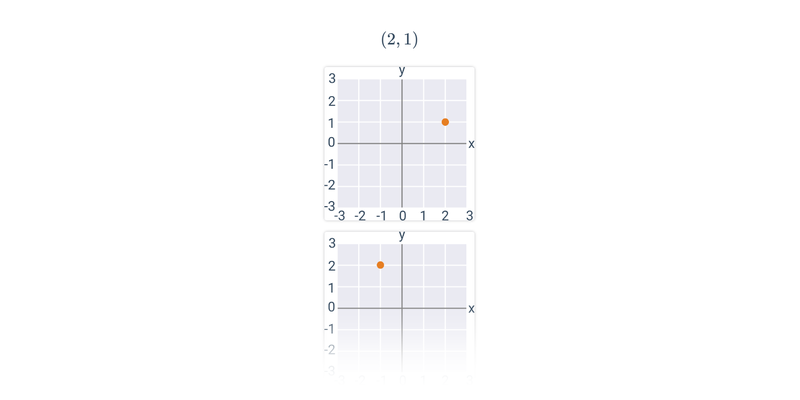
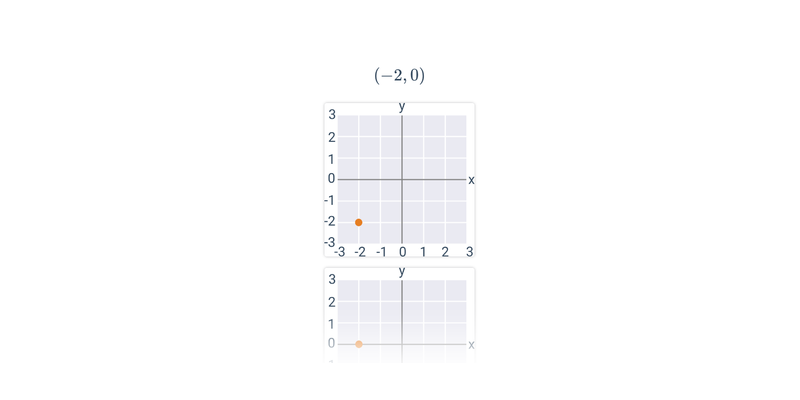
Przesuwanie

Przesuwanie karteczek w odpowiednie miejsce. Proste sterowanie, atrakcyjne i oryginalne zadania.

Geometria analityczna

Punkty

Współrzędne punktów w ukł. współrzędnych

Współrzędne punktów w ukł. współrzędnych: pierwsza ćwiartka

Współrzędne punktów w przestrzeni

Odległość między punktami w ukł. współrzędnych

Odległość między punktami w przestrzeni

Odcinki

Długość odcinka w ukł. współrzędnych

Długość odcinka w przestrzeni

Wektory

Współrzędne wektora

Długość wektora

Długość wektora w ukł. współrzędnych

Proste

Równanie parametryczne prostej w ukł. współrzędnych

Równanie ogólne prostej w ukł. współrzędnych

Krzywe stożkowe

Okrąg (krzywe stożkowe)

Okrąg: równanie kanoniczne

Elipsa

Elipsa: równanie kanoniczne

Parabola

Parabola: równania

Hiperbola

Hiperbola: równanie kanoniczne

Krzywe stożkowe: miks przykładów

Równania krzywych stożkowych

Okrąg: równanie kanoniczne

Przesuwanie • średnie

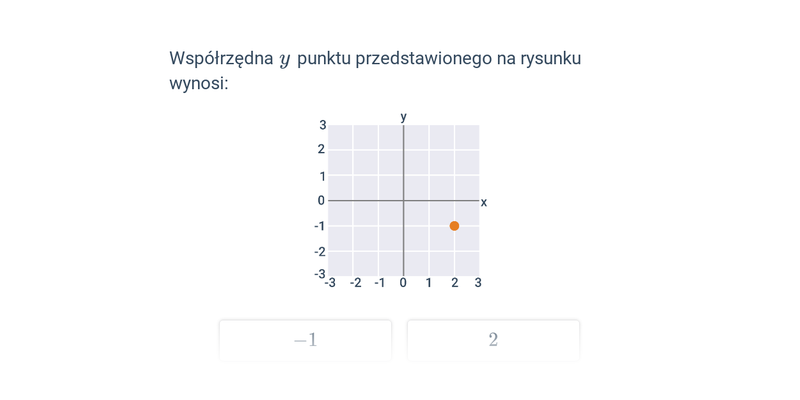
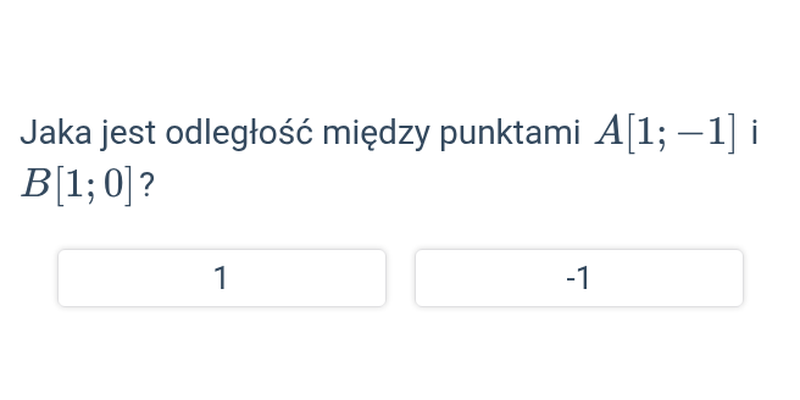
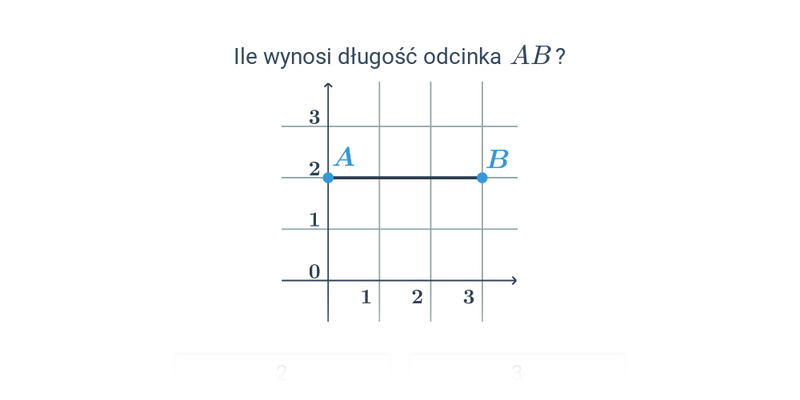
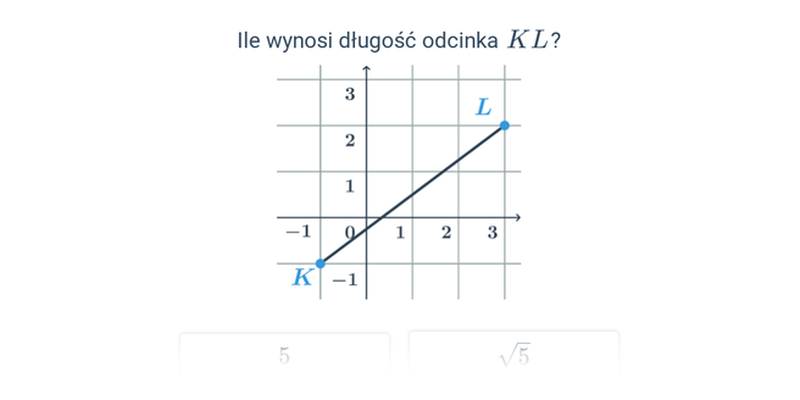
Decydowanie

Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.

Geometria analityczna

Punkty

Współrzędne punktów w ukł. współrzędnych

Współrzędne punktów w ukł. współrzędnych: pierwsza ćwiartka

Współrzędne punktów w przestrzeni

Odległość między punktami w ukł. współrzędnych

Odległość między punktami w przestrzeni

Punkty: miks przykładów

Odcinki

Długość odcinka w ukł. współrzędnych

Środek odcinka w ukł. współrzędnych

Wzajemne położenie odcinków w ukł. współrzędnych

Długość odcinka w przestrzeni

Środek odcinka w przestrzeni

Wzajemne położenie odcinków w przestrzeni

Odcinki: miks przykładów

Wektory

Wektory: pojęcia

Współrzędne wektora

Wektory: współrzędne w przestrzeni

Długość wektora

Wzajemne położenie wektorów

Wektory: miks przykładów

Działania na wektorach

Wektory: mnożenie przez stałą, suma, różnica

Wektory: iloczyn skalarny

Działania na wektorach: miks przykładów

Proste

Proste: pojęcia

Wyznaczanie prostej

Równanie ogólne prostej w ukł. współrzędnych

Wzajemne położenie prostej i punktu w ukł. współrzędnych

Proste: miks przykładów

Płaszczyzny

Wzajemne położenie punktu i płaszczyzny

Krzywe stożkowe

Krzywe stożkowe: pojęcia

Okrąg: pojęcia

Parabola: pojęcia

Okrąg (krzywe stożkowe)

Okrąg: równanie ogólne

Parabola

Parabola: równanie

Wzajemne położenie prostej i punktu w ukł. współrzędnych

Decydowanie • trudne

Wzajemne położenie prostej i punktu w ukł. współrzędnych

Memory

Szukanie pasujących par.

Geometria analityczna

Punkty

Współrzędne punktów w ukł. współrzędnych

Odcinki

Długość odcinka w ukł. współrzędnych

Długość odcinka

Wzajemne położenie odcinków w ukł. współrzędnych

Współrzędne punktów w ukł. współrzędnych

Memory • łatwe

Współrzędne punktów w ukł. współrzędnych

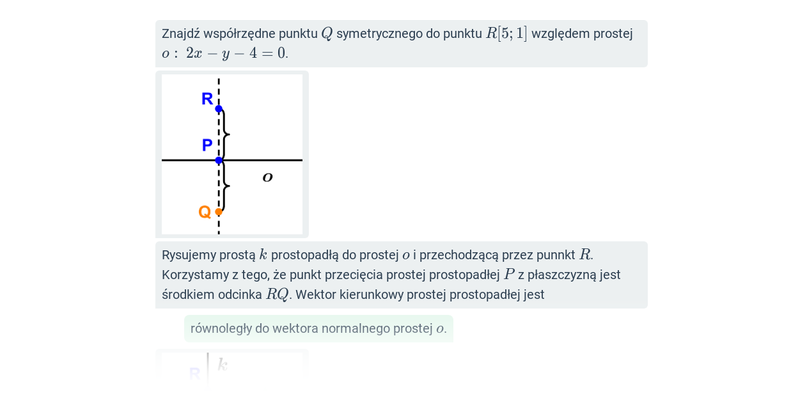
Krok po kroku

Uzupełnianie poszczególnych kroków dłuższego zadania.

Geometria analityczna

Odcinki

Środek odcinka w ukł. współrzędnych

Proste

Proste: miks przykładów

Zadania na położenie

Proste: miks przykładów

Krok po kroku • trudne

Wpisywanie odpowiedzi

Ćwiczenie, w którym wpisujesz odpowiedź na klawiaturze.

Geometria analityczna

Punkty

Współrzędne punktów w ukł. współrzędnych

Współrzędne punktów w przestrzeni

Odległość między punktami w ukł. współrzędnych

Odległość między punktami w przestrzeni

Punkty: miks przykładów

Odcinki

Długość odcinka w ukł. współrzędnych

Środek odcinka w ukł. współrzędnych

Długość odcinka w przestrzeni

Środek odcinka w przestrzeni

Odcinki: miks przykładów

Wektory

Współrzędne wektora

Długość wektora

Wzajemne położenie wektorów

Wektory: miks przykładów

Działania na wektorach

Wektory: iloczyn skalarny

Proste

Wzajemne położenie prostej i punktu w ukł. współrzędnych

Krzywe stożkowe

Okrąg (krzywe stożkowe)

Okrąg: równanie kanoniczne

Parabola

Krzywe stożkowe: miks przykładów

Wzajemne położenie wektorów

Wpisywanie odpowiedzi • trudne

Wykresownik

Specjalistyczne ćwiczenie do pracy z wykresami i funkcjami.

Geometria analityczna

Punkty

Współrzędne punktów w ukł. współrzędnych

Wykresownik • łatwe

Roboty

Wyścigi z robotami. Proste sterowanie za pomocą wyboru poprawnej odpowiedzi.

Geometria analityczna

Punkty

Współrzędne punktów w ukł. współrzędnych

Start

Filtruj według klasy

Ćwiczenia

Geometria analityczna

Przesuwanie

Okrąg: równanie kanoniczne

Decydowanie

Wzajemne położenie prostej i punktu w ukł. współrzędnych

Memory

Współrzędne punktów w ukł. współrzędnych

Krok po kroku

Proste: miks przykładów

Wpisywanie odpowiedzi

Wzajemne położenie wektorów

Wykresownik

Współrzędne punktów w ukł. współrzędnych

Roboty

Twoja wiadomość została wysłana. Dziękujemy.

Napisz do nas

Jesteś w kropce?

Wybierz temat

Filtruj według klasy

Ćwiczenia

Geometria analityczna

Przesuwanie

Współrzędne punktów w ukł. współrzędnych (średnie) • GJM

Współrzędne punktów w ukł. współrzędnych: pierwsza ćwiartka (łatwe) • G4W

Współrzędne punktów w przestrzeni (średnie) • GJ3

Odległość między punktami w ukł. współrzędnych (średnie) • GKP

Odległość między punktami w przestrzeni (średnie) • GLO

Długość odcinka w ukł. współrzędnych (średnie) • GMA

Długość odcinka w przestrzeni (średnie) • GMV

Współrzędne wektora (średnie) • GKV

Długość wektora w ukł. współrzędnych (średnie) • GKZ

Równanie parametryczne prostej w ukł. współrzędnych (średnie) • GLX

Równanie ogólne prostej w ukł. współrzędnych (średnie) • GMW

Okrąg: równanie kanoniczne (średnie) • GN1

Elipsa: równanie kanoniczne (średnie) • GOW

Parabola: równania (średnie) • GSM

Hiperbola: równanie kanoniczne (średnie) • GSA

Równania krzywych stożkowych (trudne) • FKM

Okrąg: równanie kanoniczne

Decydowanie

Współrzędne punktów w ukł. współrzędnych (łatwe) • GMJ

Współrzędne punktów w ukł. współrzędnych (średnie) • GMK

Współrzędne punktów w ukł. współrzędnych (trudne) • GJK

Współrzędne punktów w ukł. współrzędnych: pierwsza ćwiartka (łatwe) • G4D

Współrzędne punktów w przestrzeni (średnie) • GJR

Odległość między punktami w ukł. współrzędnych (łatwe) • GJS

Odległość między punktami w ukł. współrzędnych (średnie) • GJT

Odległość między punktami w przestrzeni (średnie) • GLP

Punkty: miks przykładów (łatwe) • FSX

Punkty: miks przykładów (średnie) • FSN

Długość odcinka w ukł. współrzędnych (łatwe) • GLZ

Długość odcinka w ukł. współrzędnych (średnie) • GL1

Środek odcinka w ukł. współrzędnych (łatwe) • GM3

Środek odcinka w ukł. współrzędnych (średnie) • GM4

Wzajemne położenie odcinków w ukł. współrzędnych (łatwe) • GMX

Wzajemne położenie odcinków w ukł. współrzędnych (średnie) • GMZ

Długość odcinka w przestrzeni (średnie) • GML

Środek odcinka w przestrzeni (średnie) • GNH

Wzajemne położenie odcinków w przestrzeni (trudne) • GM2

Odcinki: miks przykładów (łatwe) • FSZ

Odcinki: miks przykładów (średnie) • FNJ

Wektory: pojęcia (średnie) • FNK

Wektory: pojęcia (trudne) • GJO

Współrzędne wektora (średnie) • GKK

Współrzędne wektora (trudne) • GKL

Wektory: współrzędne w przestrzeni (średnie) • GNV

Długość wektora (średnie) • GJU

Długość wektora (trudne) • GJV

Wzajemne położenie wektorów (średnie) • GJ4

Wzajemne położenie wektorów (trudne) • GJ6

Wektory: miks przykładów (średnie) • FLW

Wektory: miks przykładów (trudne) • FLX

Wektory: mnożenie przez stałą, suma, różnica (średnie) • GKA

Wektory: mnożenie przez stałą, suma, różnica (trudne) • GKD

Wektory: iloczyn skalarny (trudne) • GJ9

Działania na wektorach: miks przykładów (trudne) • GTP

Proste: pojęcia (średnie) • GS4

Wyznaczanie prostej (średnie) • GL7

Równanie ogólne prostej w ukł. współrzędnych (średnie) • GL4

Wzajemne położenie prostej i punktu w ukł. współrzędnych (średnie) • GLV

Wzajemne położenie prostej i punktu w ukł. współrzędnych (trudne) • GLW

Proste: miks przykładów (średnie) • FS1

Proste: miks przykładów (trudne) • FLZ

Wzajemne położenie punktu i płaszczyzny (trudne) • GOB

Okrąg: pojęcia (średnie) • GON

Parabola: pojęcia (średnie) • GOG

Okrąg: równanie ogólne (średnie) • GNU

Parabola: równanie (średnie) • GOJ

Wzajemne położenie prostej i punktu w ukł. współrzędnych

Memory

Współrzędne punktów w ukł. współrzędnych (łatwe) • EDX

Współrzędne punktów w ukł. współrzędnych (średnie) • GKR

Długość odcinka (średnie) • GL9

Wzajemne położenie odcinków w ukł. współrzędnych (średnie) • GM1

Współrzędne punktów w ukł. współrzędnych

Krok po kroku

Środek odcinka w ukł. współrzędnych (łatwe) • GNA

Proste: miks przykładów (trudne) • FMA