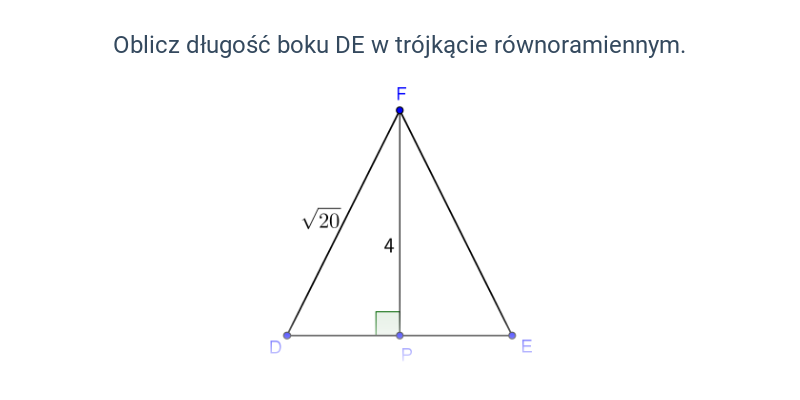
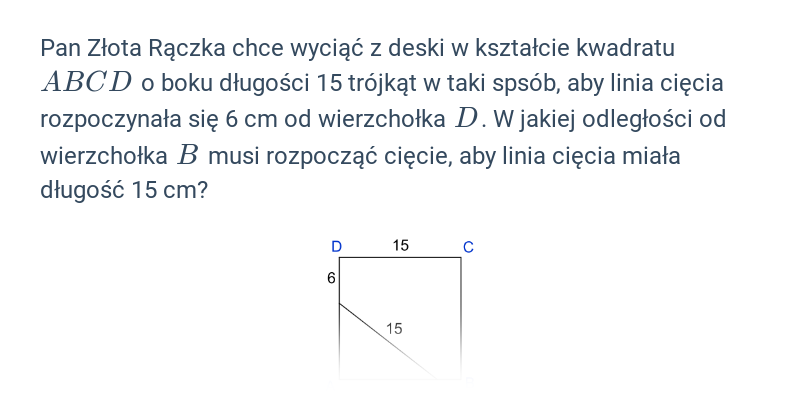
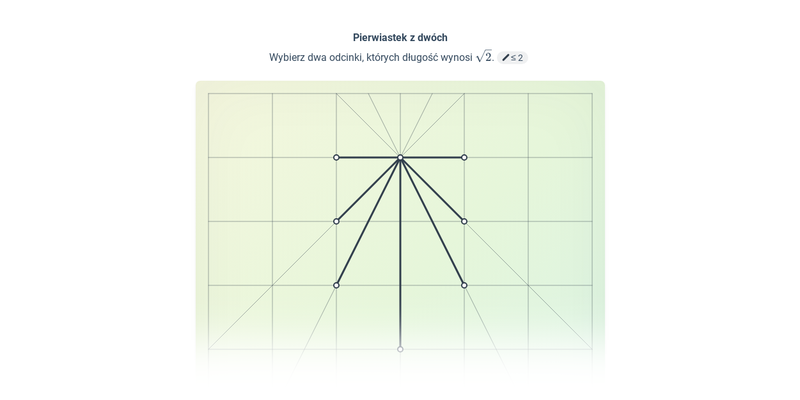
Twierdzenie Pitagorasa – Klasa 3 szkoły średniej

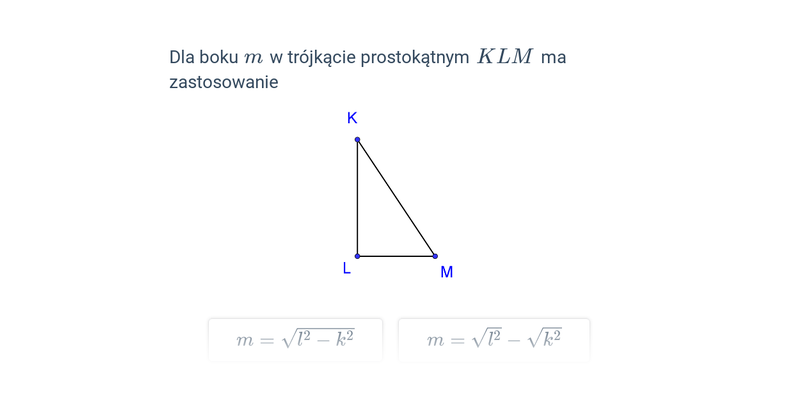
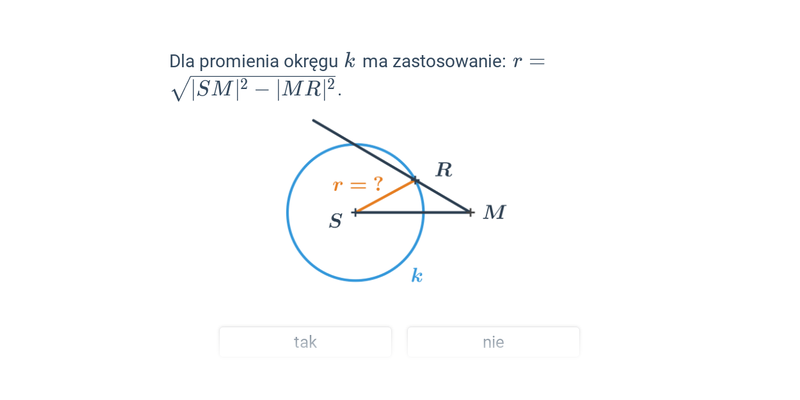
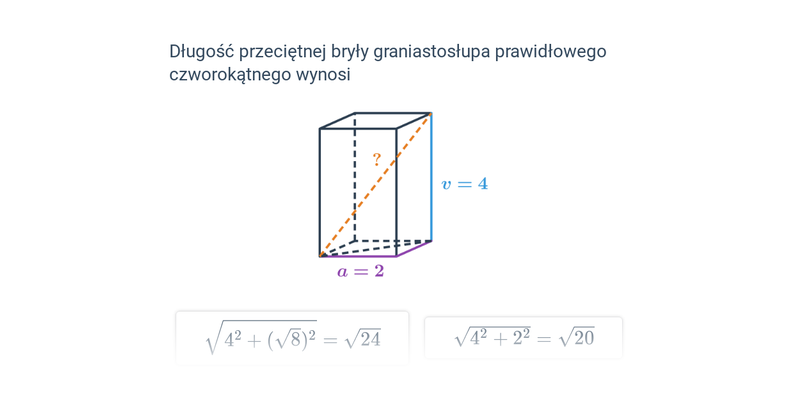
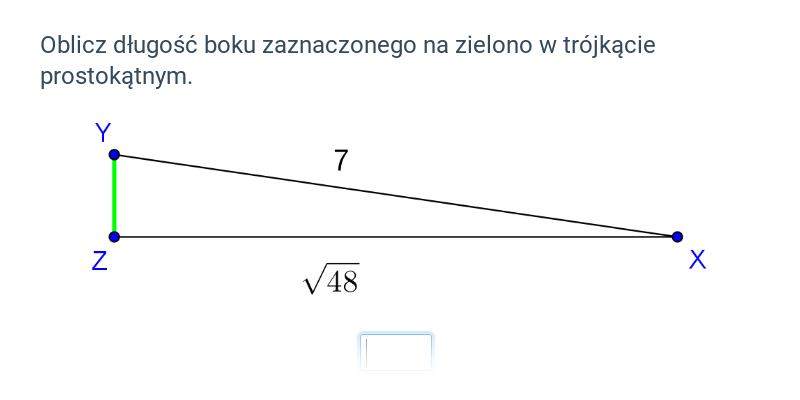
Twierdzenie Pitagorasa opisuje zależność pomiędzy długościami boków trójkąta prostokątnego. Brzmi ono: Jeśli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Oznacza to, że jeżeli na bokach trójkąta prostokątnego zbudujemy kwadraty, to suma pól kwadratów zbudowanych na przyprostokątnych tego trójkąta będzie równa polu kwadratu zbudowanego na przeciwprostokątnej. Twierdzenie Pitagorasa możemy zapisać w następujący sposób c^2 = a^2 + b^2, gdzie c to długość przeciwprostokątnej, a a i b to długości przyprostokątnych.

Poniższy rysunek to tzw. graficzny dowód twierdzenia Pitagorasa:

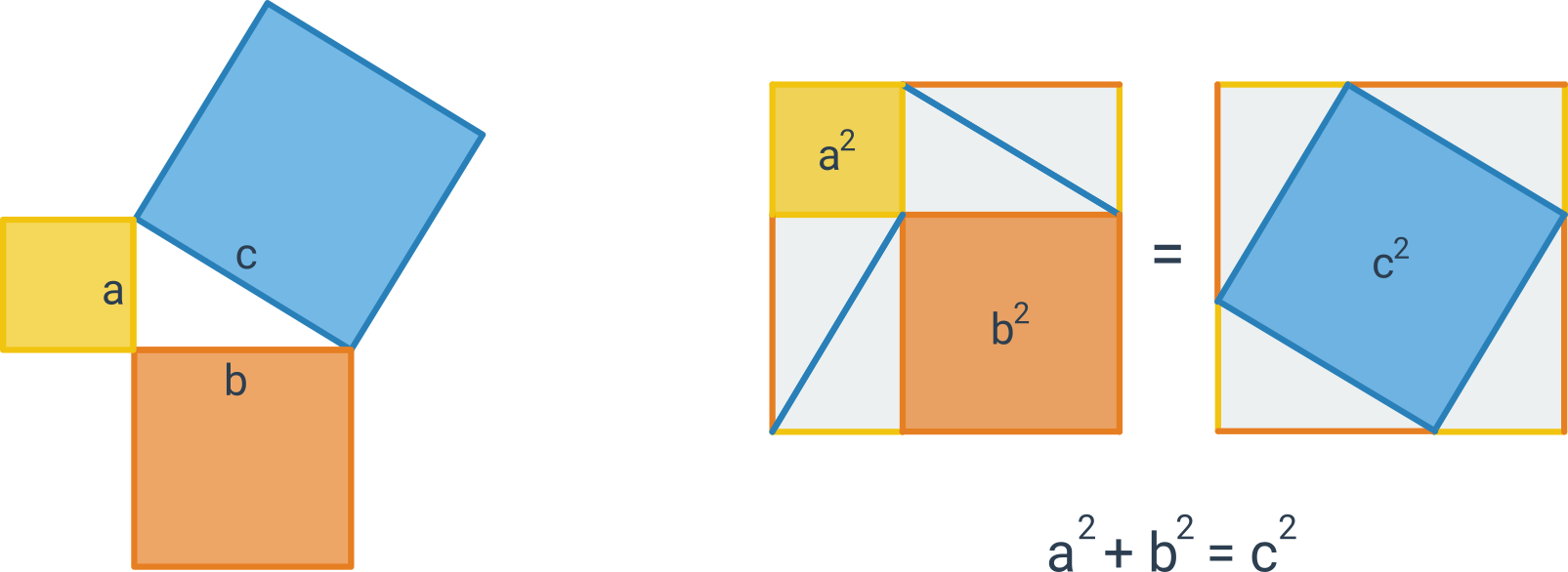
Znajduje on zastosowanie również w odwrotnym kierunku. Jeżeli suma kwadratów długości dwóch krótszych boków jest równa kwadratowi długości najdłuższego boku, to trójkąt jest prostokątny.