Dodawanie i odejmowanie ułamków zwykłych – klasa 5

Na początek przypomnijmy sobie, co jest licznikiem („to na górze“), a co mianownikiem („to na dole“). W ułamku \frac{3}{7} 3 to licznik, a 7 mianownik.

Dodawanie ułamków o tych samych mianownikach

Jeżeli ułamki, które chcemy dodać do siebie, mają taki sam mianownik, sprawa jest prosta – wystarczy dodać liczniki. Mianownik pozostawiamy bez zmian, czyli \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.

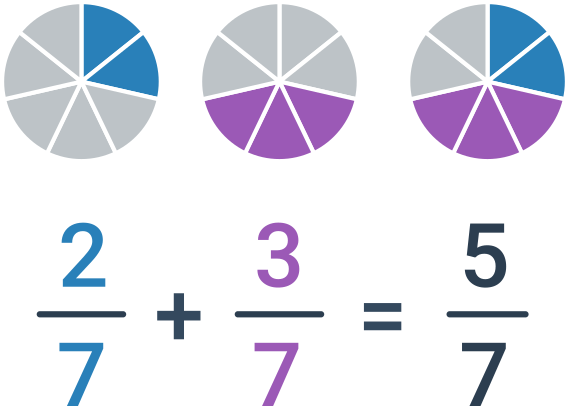
Dodawanie ułamków o różnych mianownikach

Jeżeli ułamki, które chcemy dodać do siebie, mają różne mianowniki, musimy je najpierw sprowadzić do wspólnego mianownika. Aby rozszerzyć ułamki do wspólnego mianownika, należy znaleźć najmniejszą wspólną wielokrotność mianowników. Następnie możemy dodać ułamki w sposób opisany powyżej.

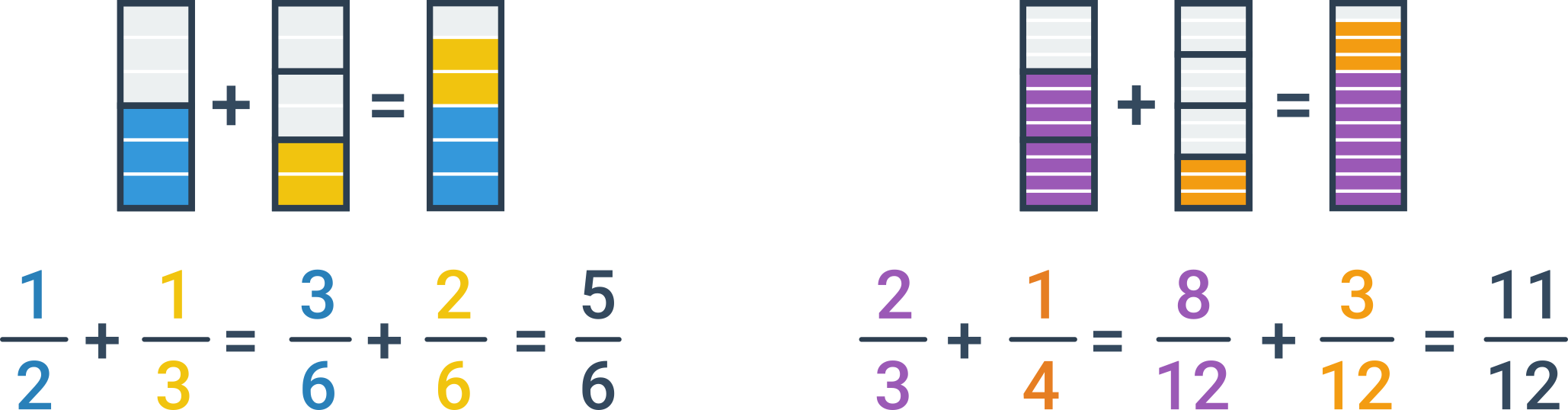
Przekształcanie i odejmowanie

Otrzymany ułamek najczęściej należy jeszcze doprowadzić do najprostszej postaci, czyli skrócić. Odejmowanie ułamków wykonujemy podobnie jak dodawanie.

Przykłady

• Ułamki o tych samych mianownikach, bez skracania wyniku:
  \frac{2}{5}+\frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}.

• Ułamki o tych samych mianownikach, wynik skracamy:
  \frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}.

• Ułamki o różnych mianownikach: \frac{5}{6} - \frac{3}{4}.
  Najmniejsza wspólna wielokrotność mianowników 6 i 4 to 12, czyli rozszerzamy ułamki do mianownika 12:
  \frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}