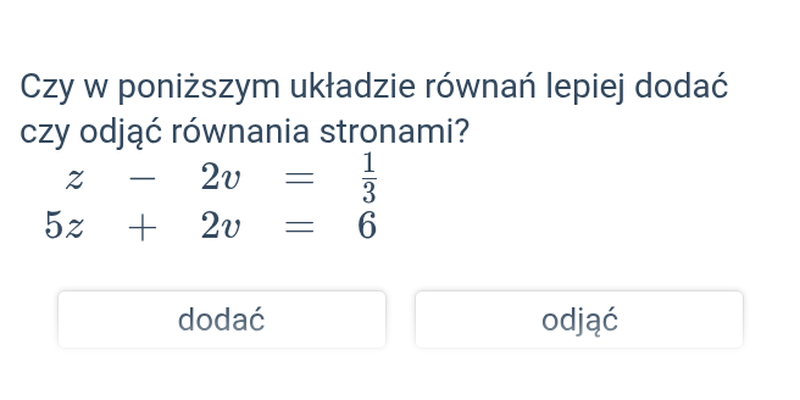
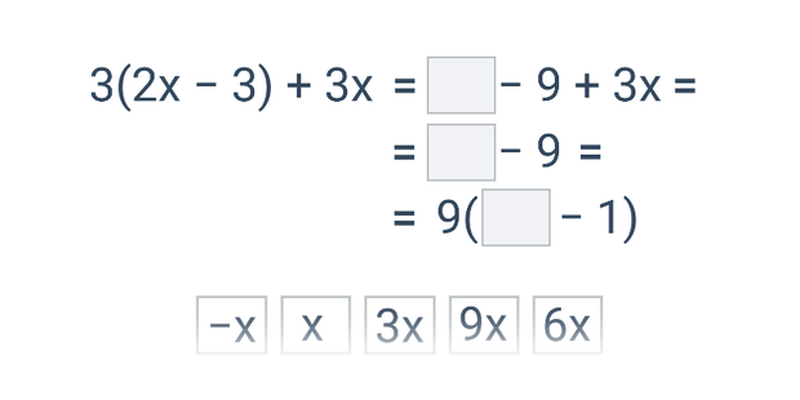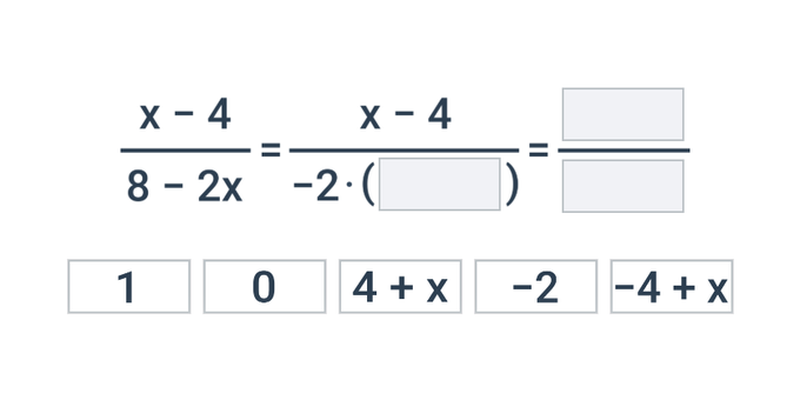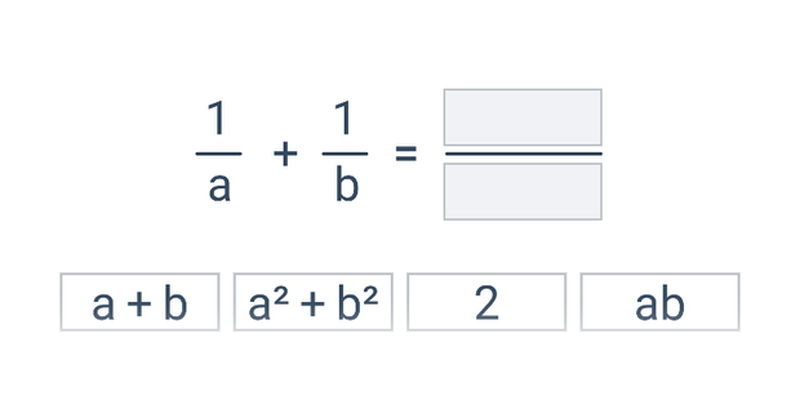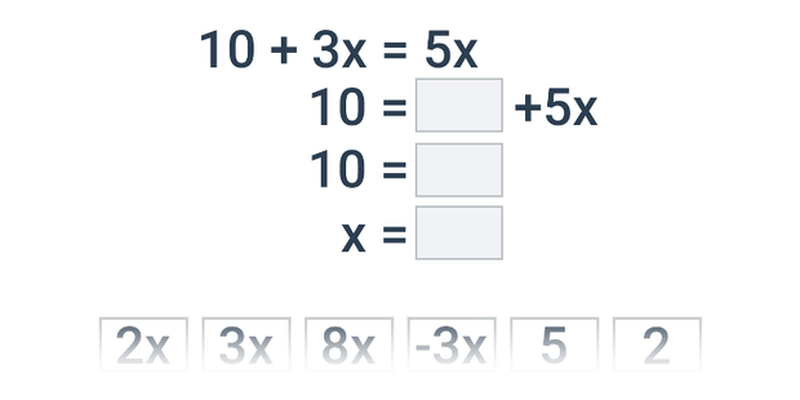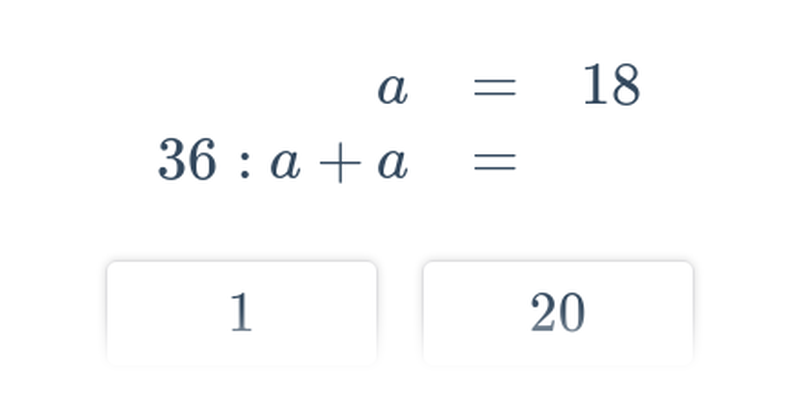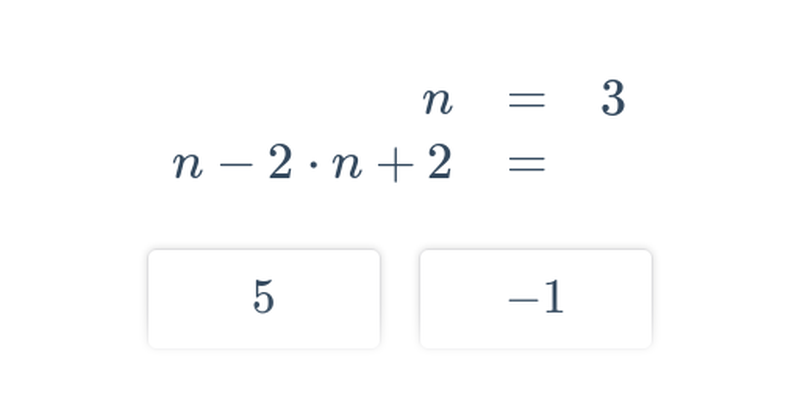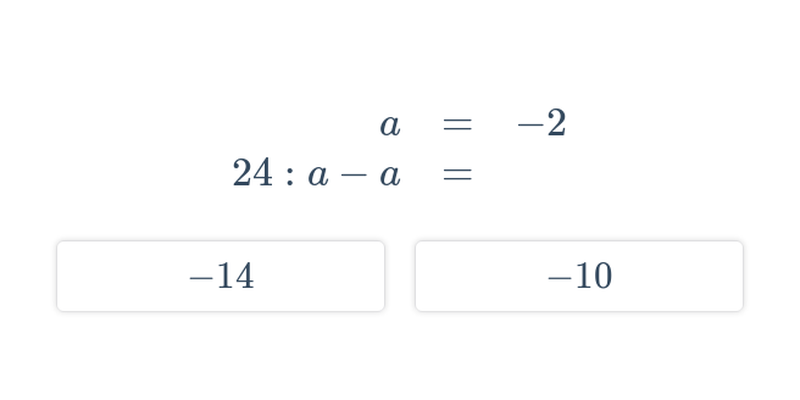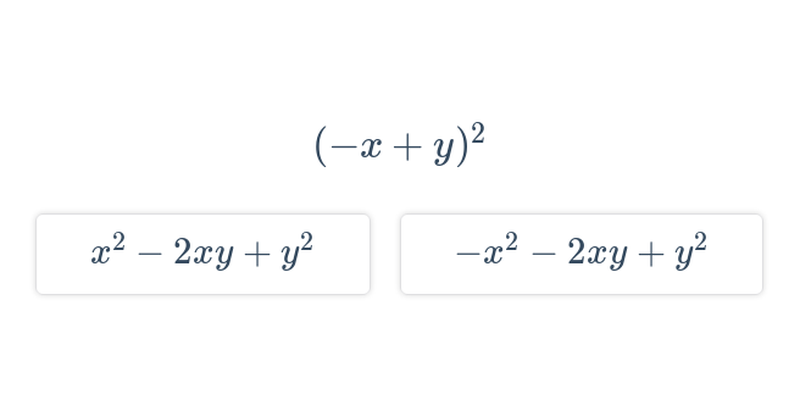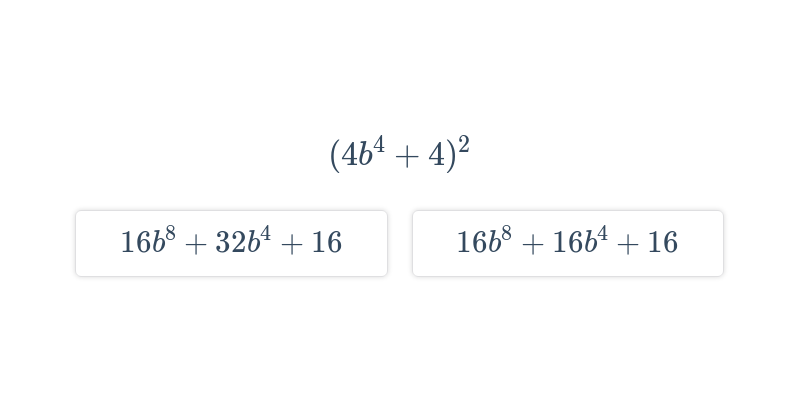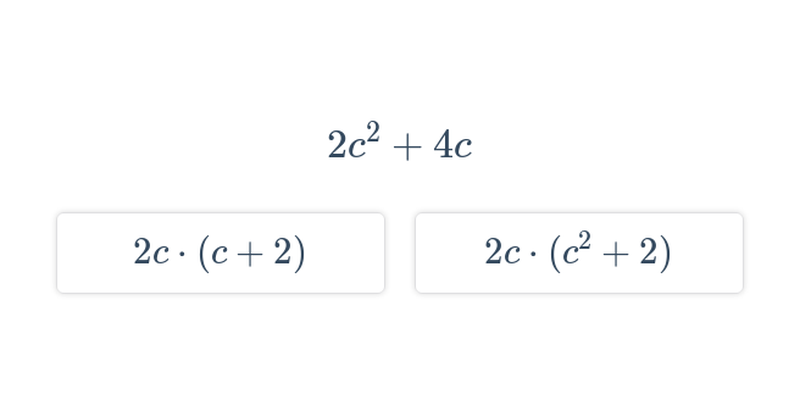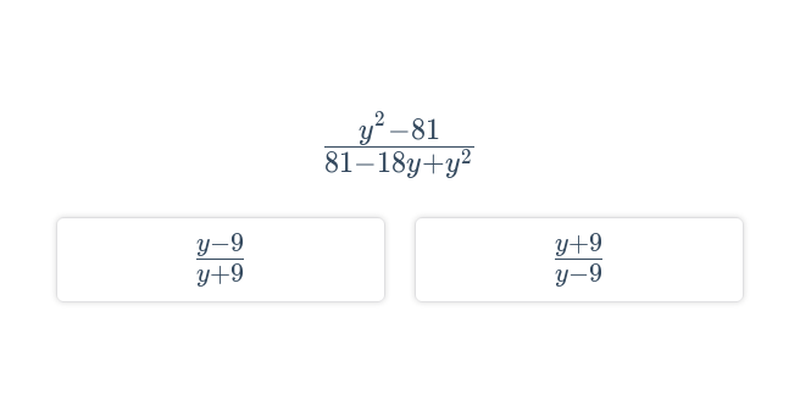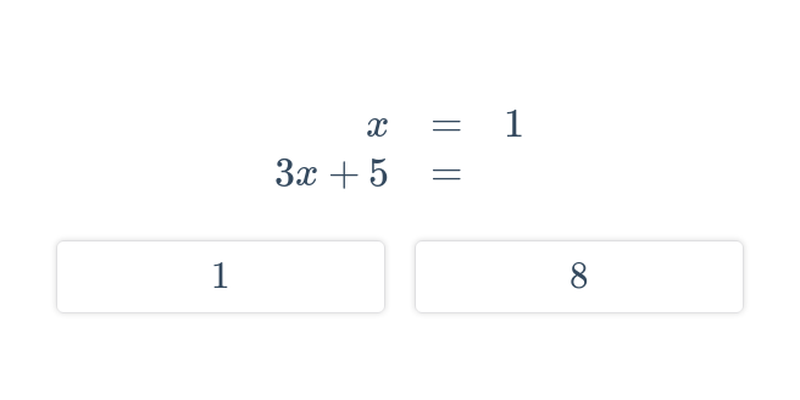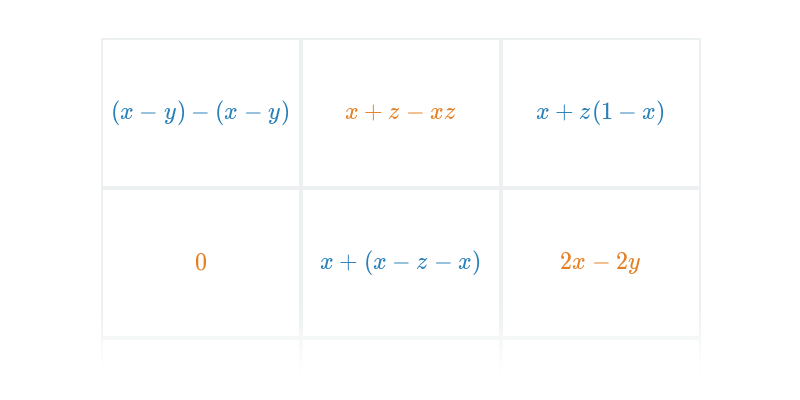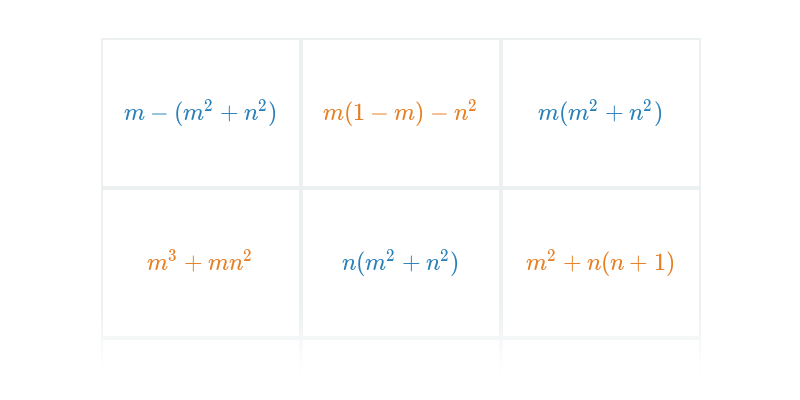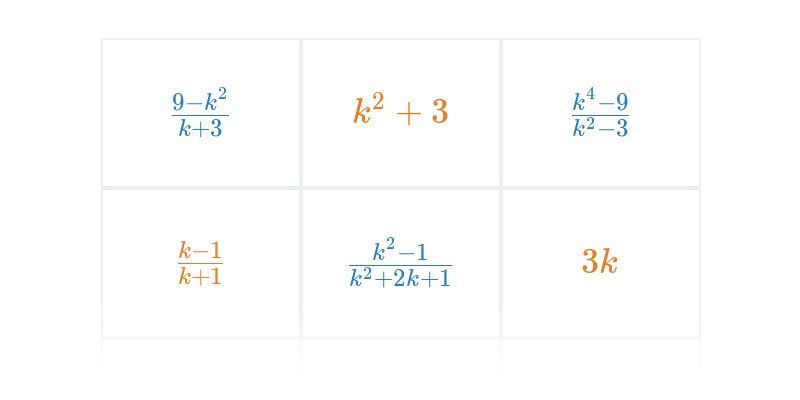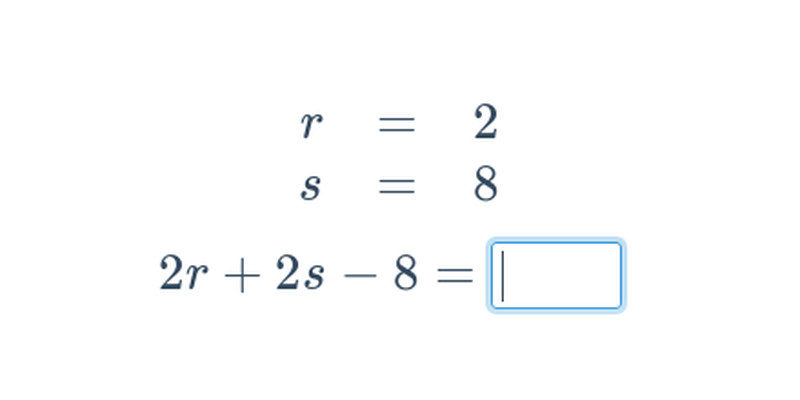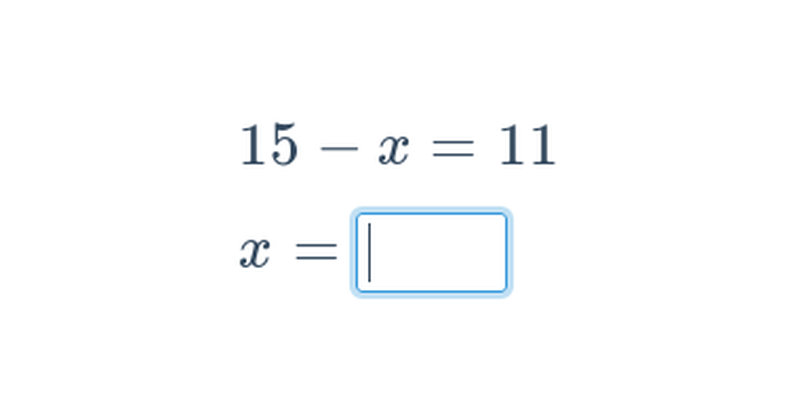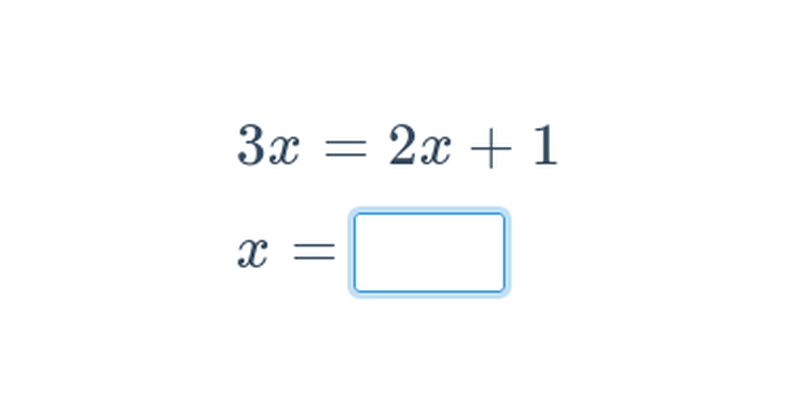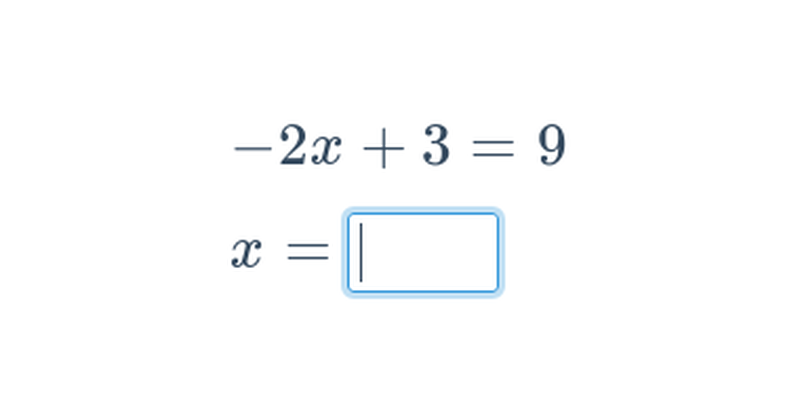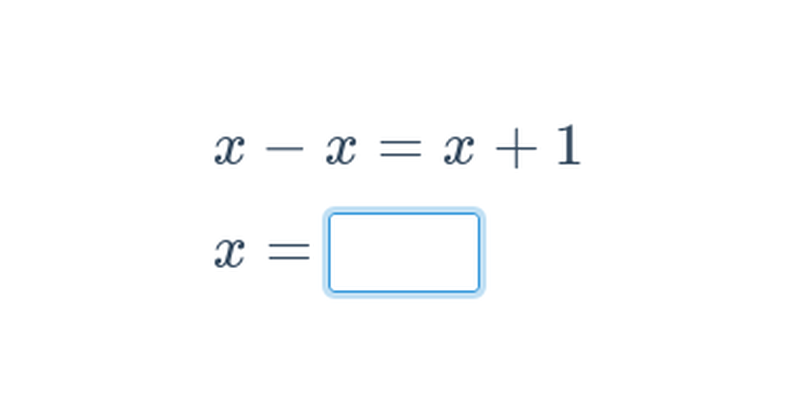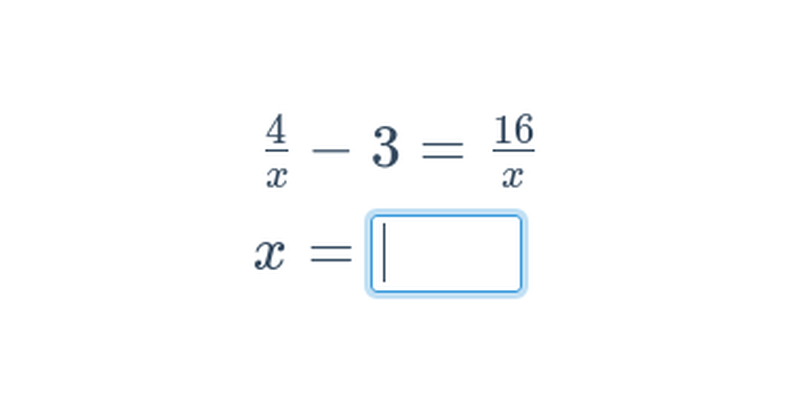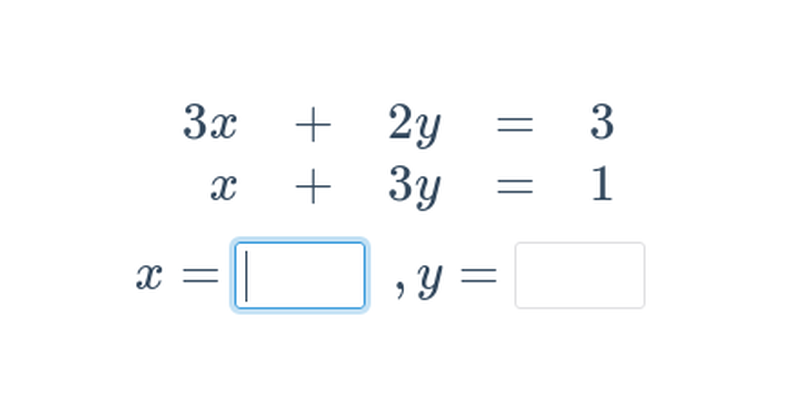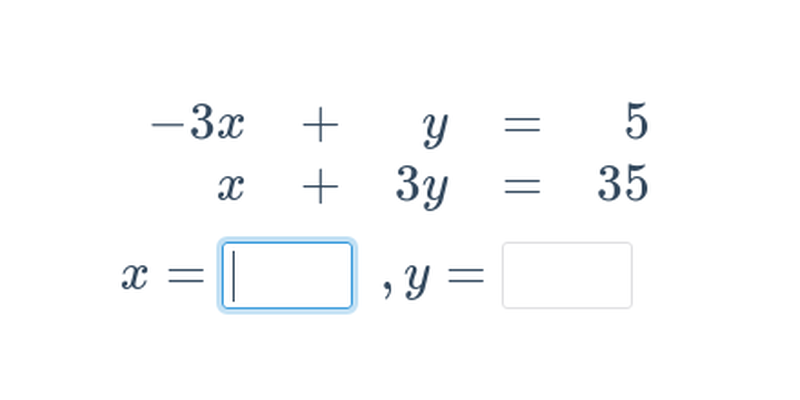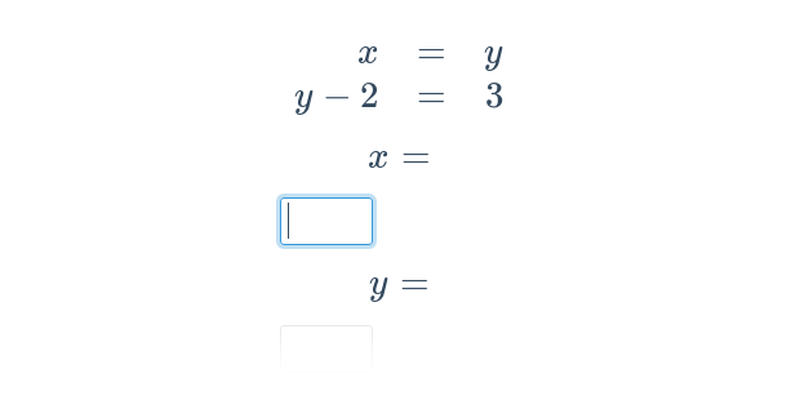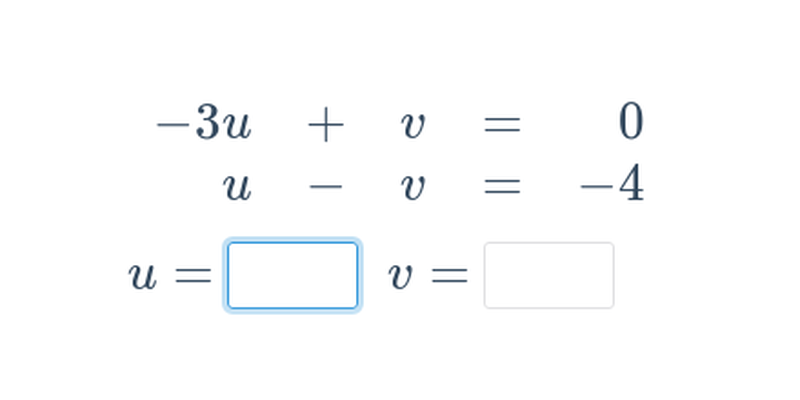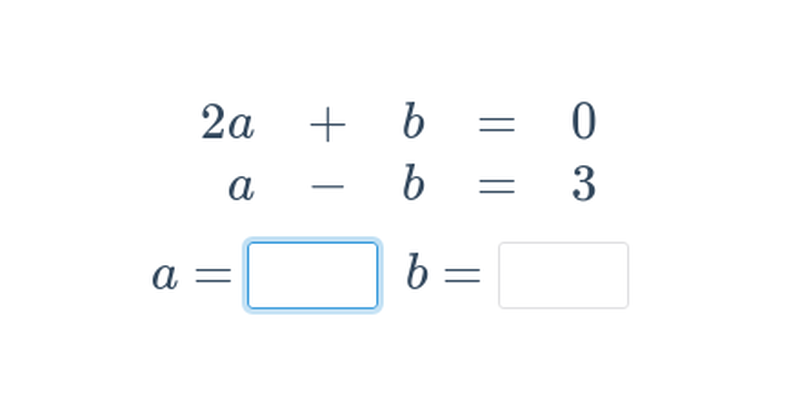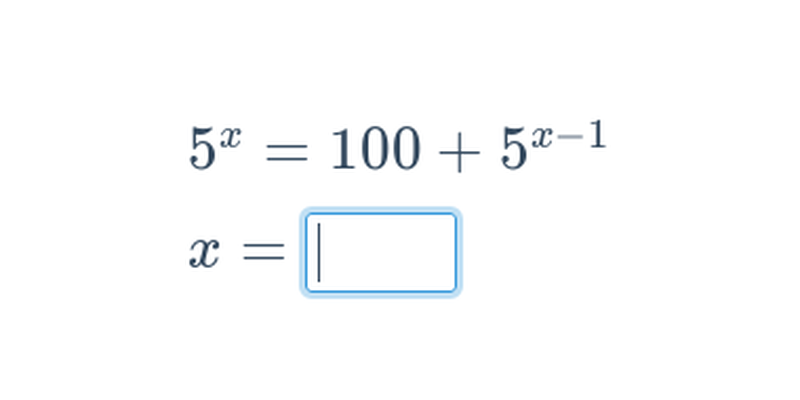Decydowanie
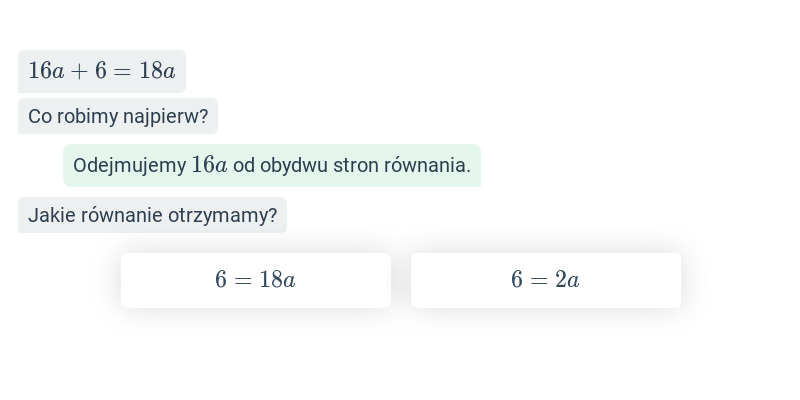
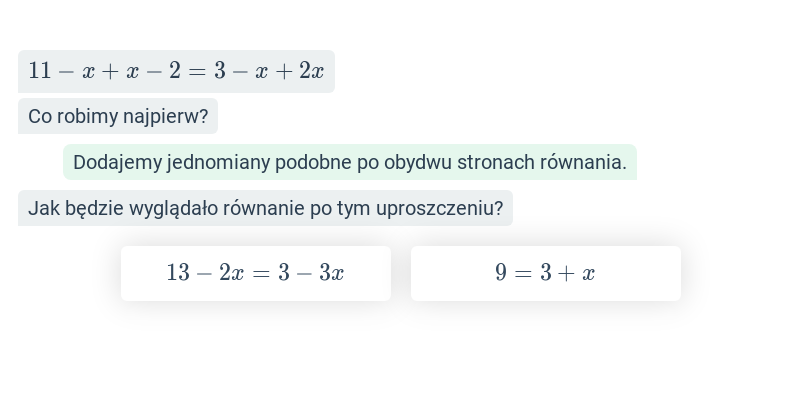
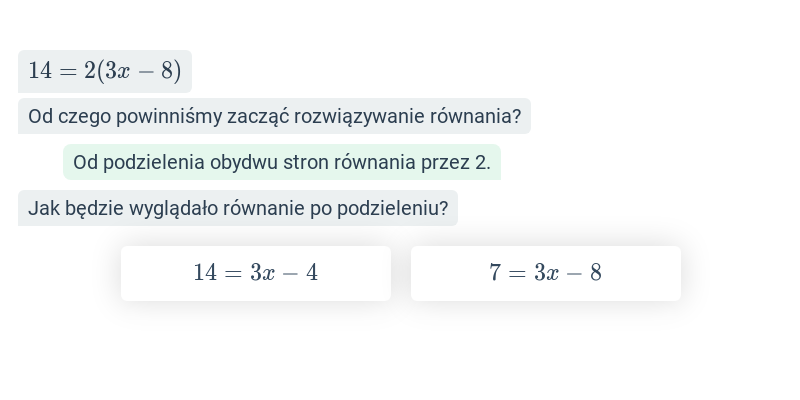
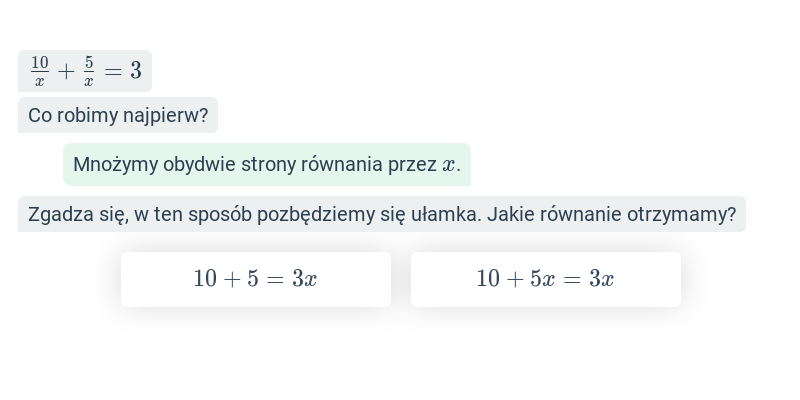
Szybkie ćwiczenie polegające na wybraniu prawidłowej odpowiedzi spośród dwóch propozycji.
Wyrażenia algebraicze, równania, nierówności
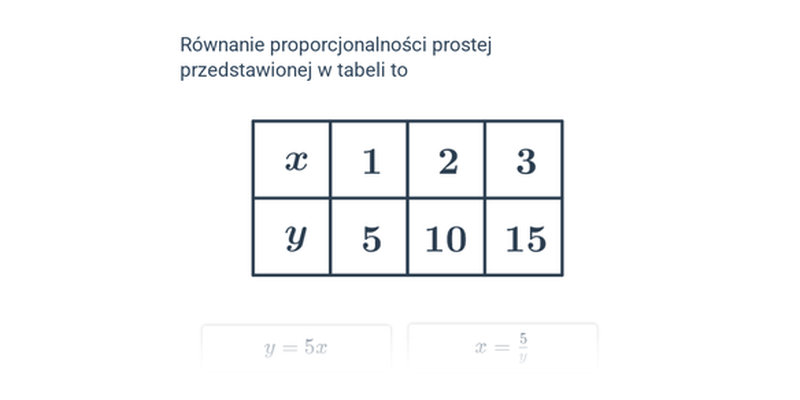
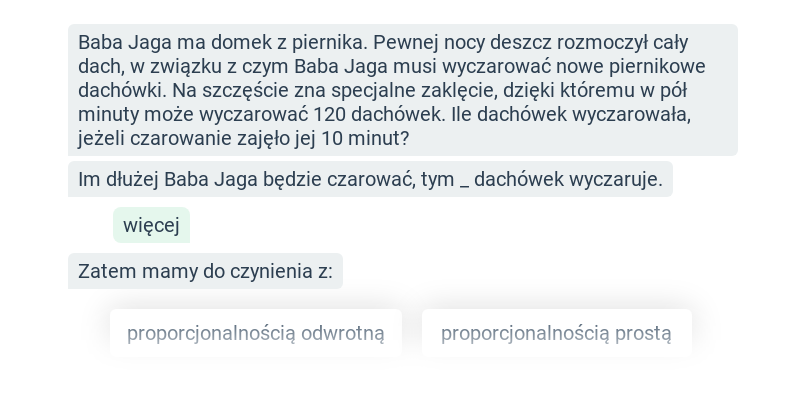
Proporcjonalność
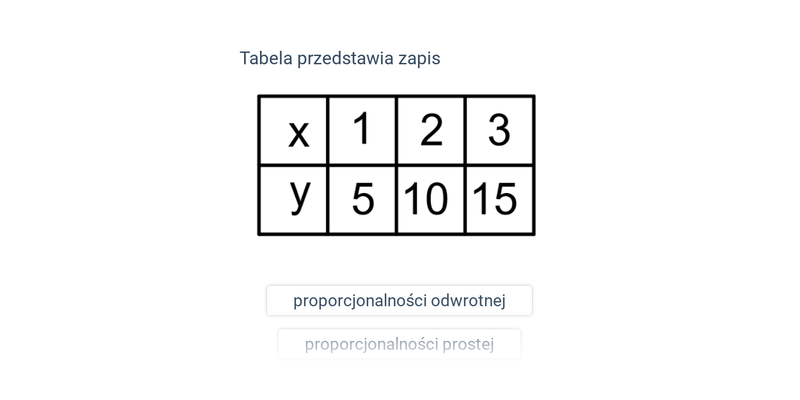
Proporcjonalność prosta i odwrotna
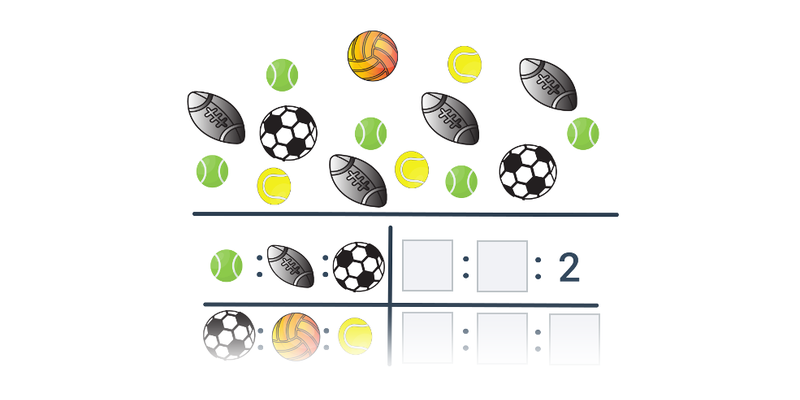
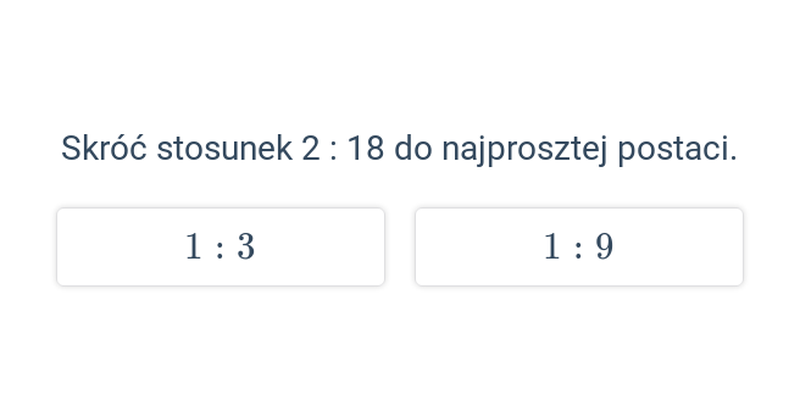
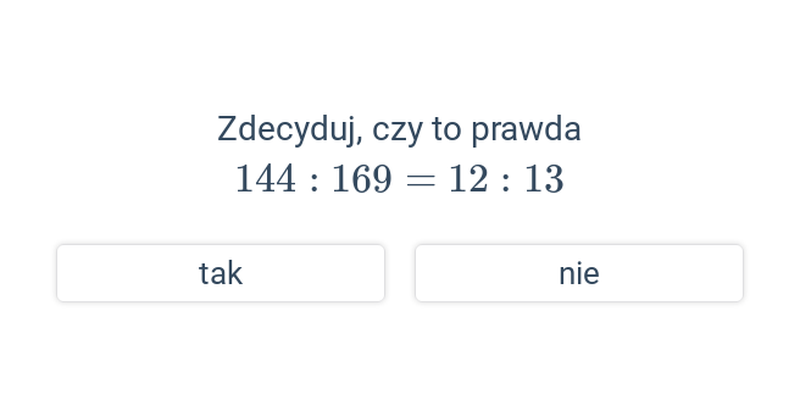
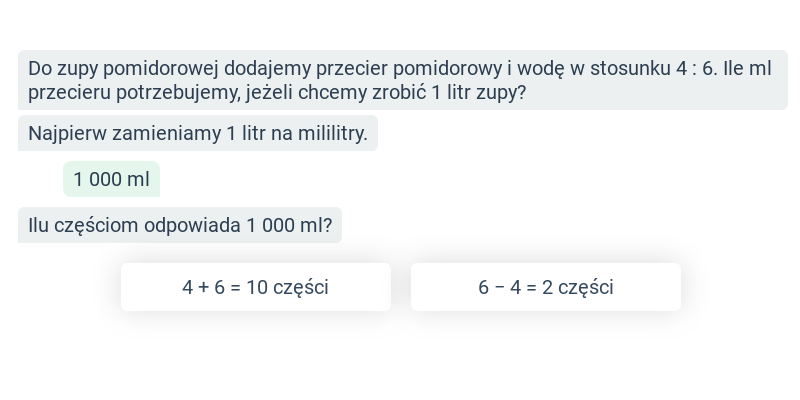
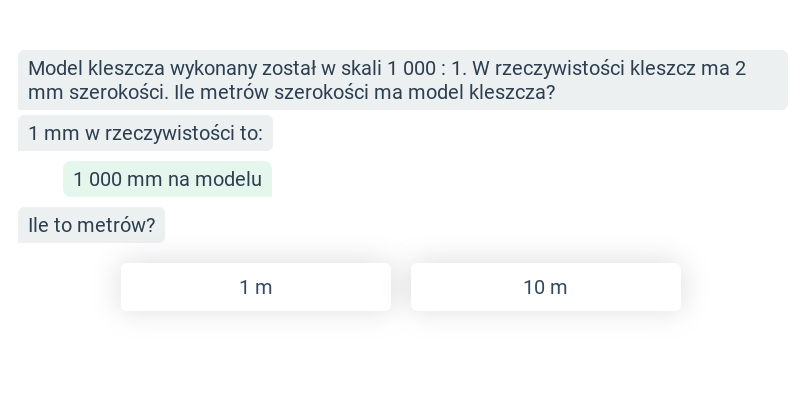
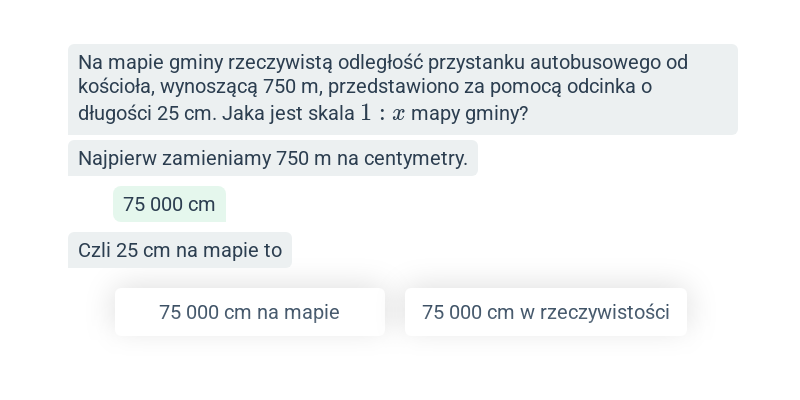
Stosunek dwóch wielkości
Stosunek dwóch wielkości: podstawy
Stosunek dwóch wielkości: obliczenia
Wyrażenia algebraiczne i ich przekształcanie
Podstawianie do wyrażeń

Zapisywanie za pomocą wyrażeń
Zapisywanie wyrażeń ze zmiennymi
Zapisywanie poleceń za pomocą wyrażeń
Upraszczanie wyrażeń z jedną niewiadomą

Upraszczanie wyrażeń z wieloma niewiadomymi

Upraszczanie wyrażeń: potęgowanie potęgi
Rozkład na czynniki
Upraszczanie wyrażeń z ułamkami zwykłymi

Wyrażenia wymierne
Dziedzina wyrażenia wymiernego
Wyrażenia wymierne: upraszczanie i działania
Przekształcanie wyrażeń wymiernych
Wyrażenia z silnią i symbolami Newtona
Przekształcanie wyrażeń z silnią
Przekształcanie wyrażeń z symbolem Newtona
Wyrażenia i ich przekształcanie: miks przykładów
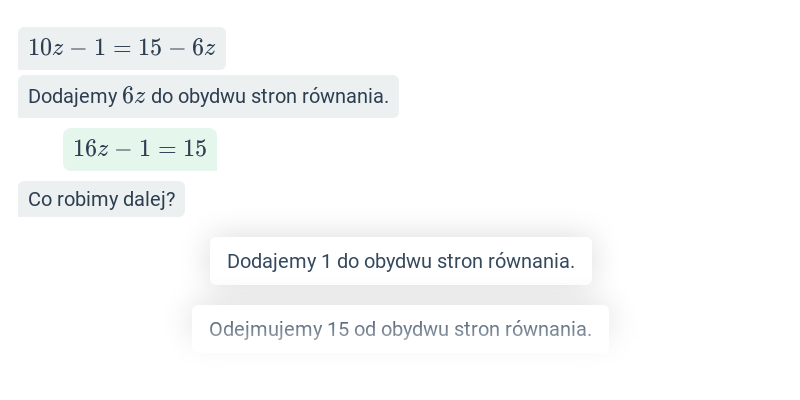
Równania zaawansowane
Dwa równania z dwoma niewiadomymi
Rozwiązywanie metodą podstawiania i przeciwnych współczynników
Zadania z równaniami
Zapisywanie treści zadania za pomocą równania
Nierówności
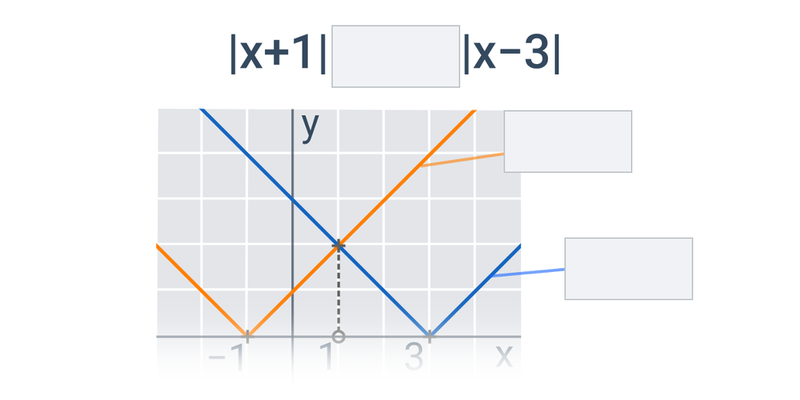
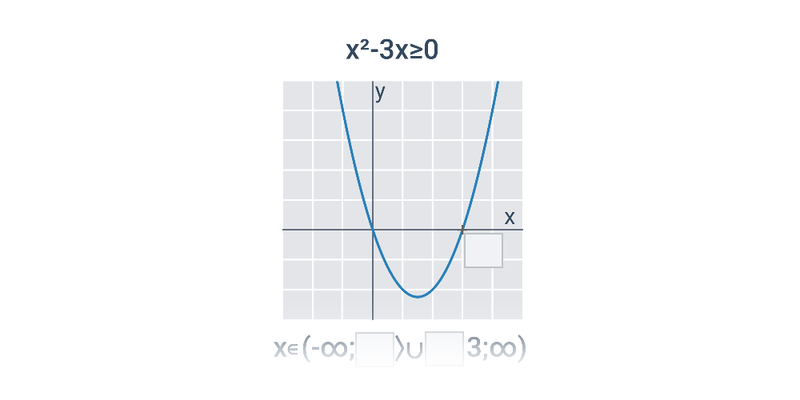
Nierówności: zapis rozwiązania
Nierówności: przekształcanie równoważne
Ciągi i szeregi
Ciąg arytmetyczny i geometryczny
Zapis ciągów